3 6
20
50
100
200
500
1k
2k
5k
10k
20k
40k
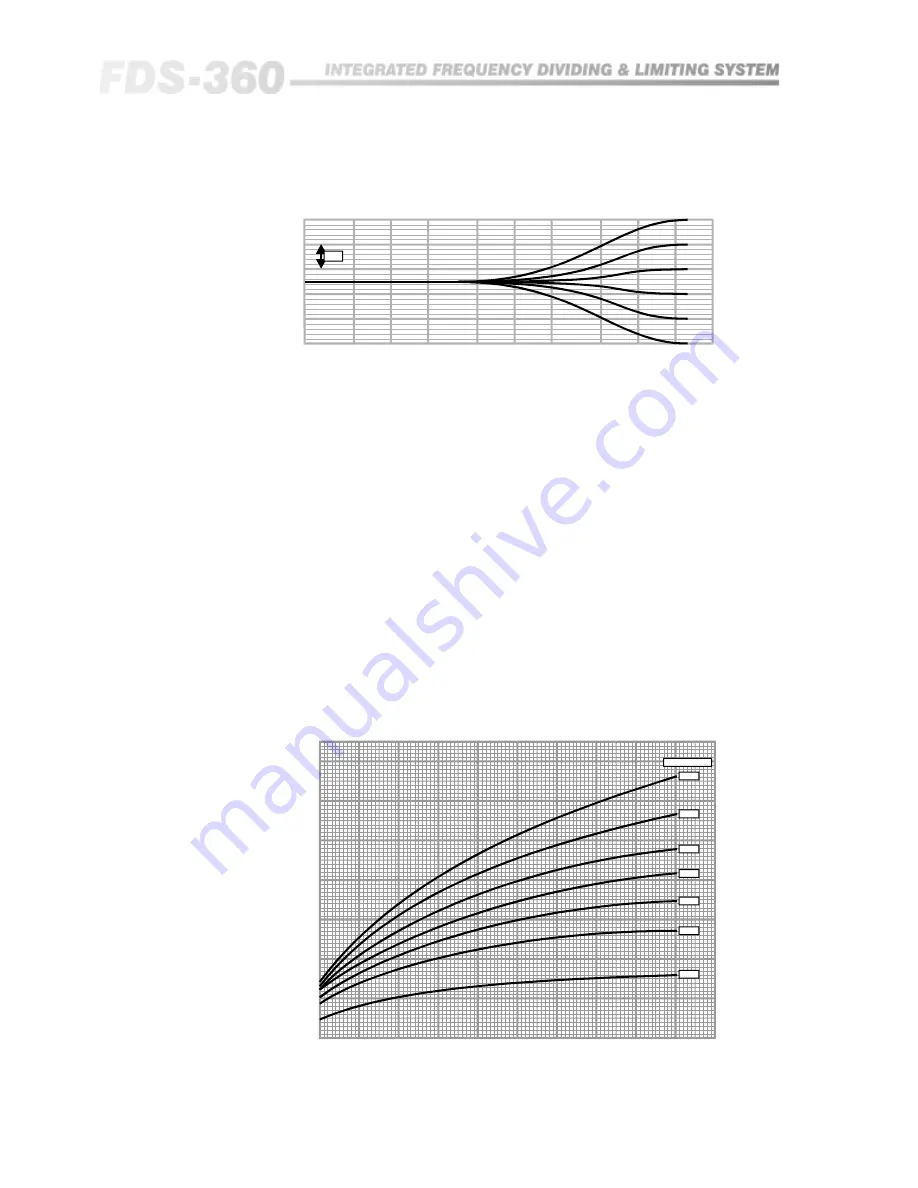
5dB
HF Shelf RQ = 0, Fc = 16kHz
Frequency (Hz)
20.6 Application of
the FDS-360D to a
system
A target response should be arrived at by either inspection from a set of
frequency response curves, or by adjustment of an external equaliser
connected into the system. For simplicity, only one frequency band of the
crossover has been considered.
Take a plot of the unmodified frequency response of the
FDS-360
and on the
same sheet of graph paper plot the target response. A third plot is then drawn,
which is the difference, in dBs, between the two curves and this 'correction'
curve is the desired response of the
FDS-360
equalisation section. From this
correction curve, the amount of dB boost or cut and the centre frequency, Fc,
are easily obtained by inspection. The required Q value can either be
obtained by calculation or estimated by comparison with the sample curves
provided with this manual.
The equation of Q of a Bell response curve is:
Q = Fc/(Fu - Fl),
where Fu and Fl are the frequencies at which the amplitude response is 3dB
down from the value at Fc.
0
1k
2k
3k
4k
5k
6k
7k
8k
9k
10k
0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
2.2
2.4
2.6
2.8
3.0
Q
RQ (ohms)
16dB
14dB
12dB
10dB
8dB
6dB
4dB
Q vs RQ for Various Degrees of Boost/Cut
FDS-360D
dB Boost/Cut
Fig 20.8 Sample HF
Shelving Response
Curves
Fig 20.9 Design Curves
for Rq.
Equalisation Options
Содержание FDS 360
Страница 1: ...1 FDS 360 User Manual...
Страница 51: ...51 User Notes...
Страница 52: ...52 User Notes...
Страница 53: ...53...
Страница 54: ...54 User Notes...