AD9854
Rev. E | Page 23 of 52
F1
F2
0
F
RE
Q
UE
NC
Y
MODE
TW1
TW2
FSK DATA
TRIANGLE
BIT
010 (RAMPED FSK)
F1
F2
I/O UD CLK
006
36
-04
0
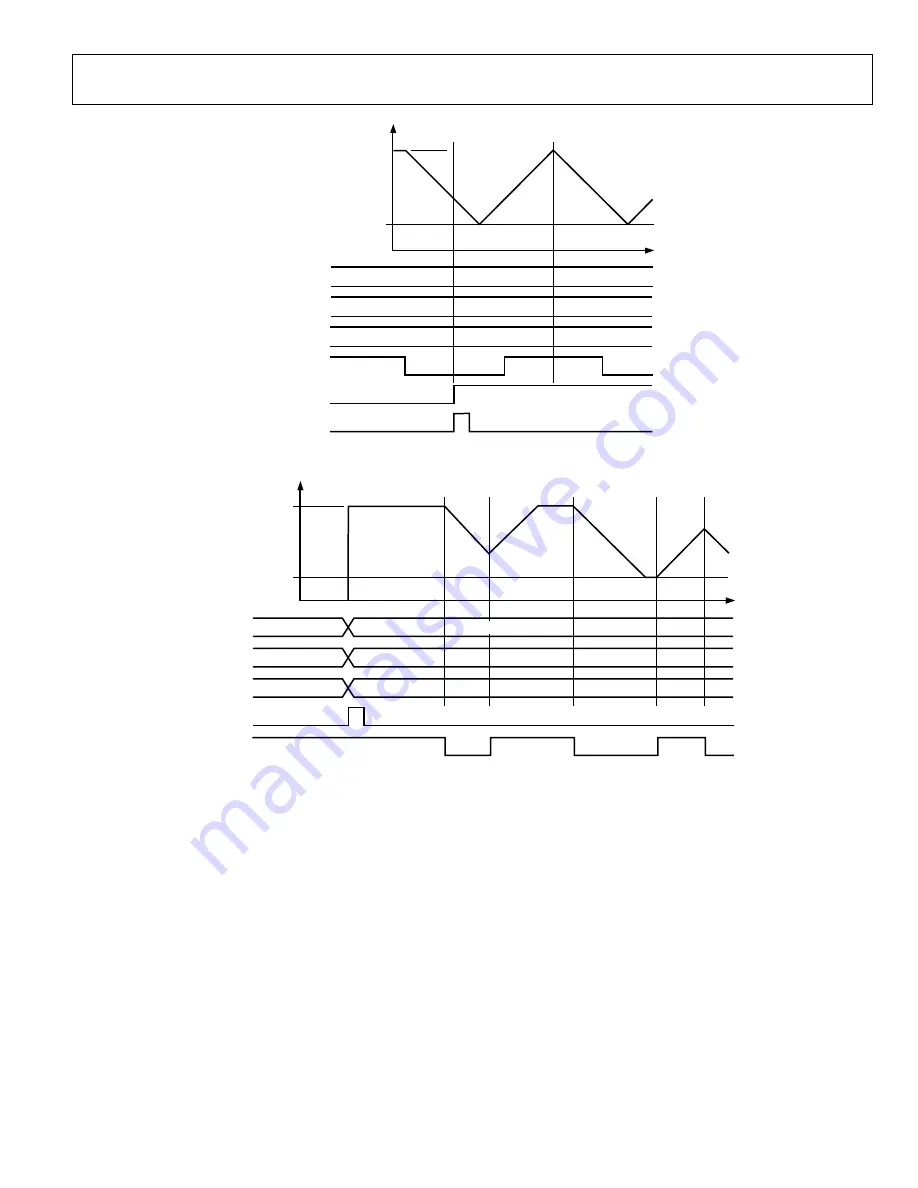
Figure 40. Effect of Triangle Bit in Ramped FSK Mode
F1
F2
0
F
RE
Q
UE
NC
Y
MODE
TW1
TW2
FSK DATA
F1
F2
000 (DEFAULT)
0
0
010 (RAMPED FSK)
I/O UD CLK
00
63
6-
0
41
Figure 41. Effect of Premature Ramped FSK Data
Figure 41 shows that premature toggling causes the ramp to
immediately reverse itself and proceed at the same rate and
resolution until the original frequency is reached.
The control register contains a triangle bit at Parallel Register
Address 1F hex. Setting this bit high in Mode 010 causes an
automatic ramp-up and ramp-down between F1 and F2 to
occur without toggling Pin 29, as shown in Figure 40. The logic
state of Pin 29 has no effect once the triangle bit is set high. This
function uses the ramp rate clock time period and the step size
of the delta frequency word to form a continuously sweeping
linear ramp from F1 to F2 and back to F1 with equal dwell
times at every frequency. Use this function to automatically
sweep between any two frequencies from dc to Nyquist.
In the ramped FSK mode with the triangle bit set high, an
automatic frequency sweep begins at either F1 or F2, according
to the logic level on Pin 29 (FSK input pin) when the triangle
bit’s rising edge occurs (Figure 42). If the FSK data bit is high
instead of low, F2, rather than F1, is chosen as the start frequency.
Additional flexibility in the ramped FSK mode is provided by
the AD9854’s ability to respond to changes in the 48-bit delta
frequency word and/or the 20-bit ramp rate counter at any time
during the ramping from F1 to F2 or vice versa. To create these
nonlinear frequency changes, it is necessary to combine several
linear ramps with different slopes in a piecewise fashion. This is
done by programming and executing a linear ramp at a rate or
slope and then altering the slope (by changing the ramp rate
clock or delta frequency word, or both). Changes in slope can
be made as often as needed before the destination frequency has
been reached to form the desired nonlinear frequency sweep
response. These piecewise changes can be precisely timed using
















































