SV SLA-PA201, Manual

Page: 22 / 88

22
Generally, the time constant is set with 0.035sec(Impulse), 0.125sec(Fast), 1sec(Slow). Each term
of times writes in the parenthesis. If you want to measure the impulse signal, you have to use 0.035
sec time constant. If you use more time constant (more than 10sec), the RMS has crushed values and
the response time is also slow.
o
t
τ
Linear Averaging
Averaging Time
Exponential(
τ
=RC) Averaging
t
0
t T
−
[Fig. IV-1-2] Running RMS Calculation with Exponential Averaging
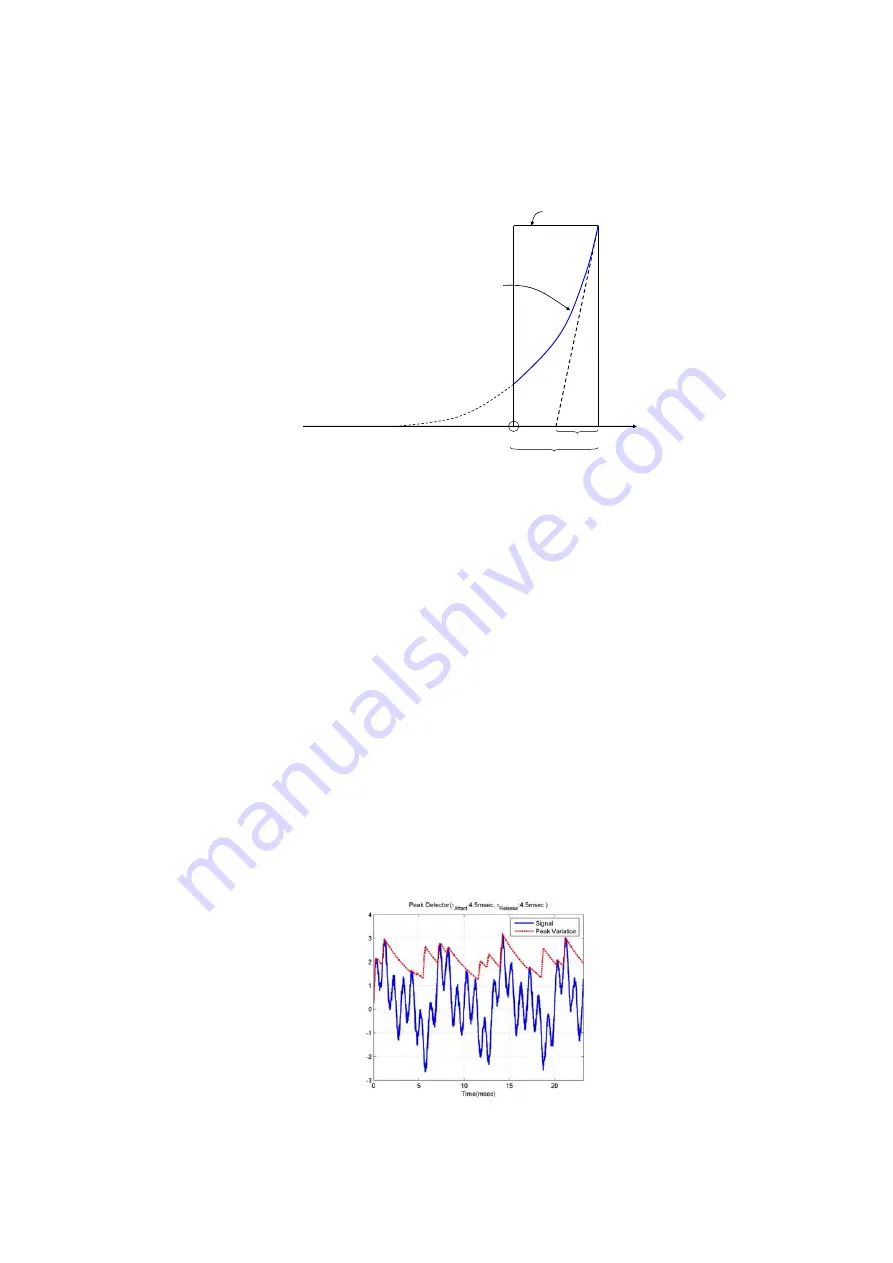
1. 2 Detector with Exponential Averaging Function
The full procedure of RMS(Root-Mean-Square) Detector is described in [1. 1] paragraph. When
peak values are calculated, we also use Peak Detector with exponential averaging. [Fig. IV-1-3]
shows how to detect peak values in real-time.
Peak Detector has two time constants. One is the attack time constant and another is the release (or
decay) time constant. The attack time constant means how peak values increase quickly. And the
release time constant means how the peak values decrease slowly after a peak.
Both time constants are defined from the user definable time constant in the program. If the release
time constant is smaller than 1.5sec, this is set by 1.5sec automatically which is defined in
“BS60651(IEC60651:1979) – Specification for Sound Level Meters”.
[Fig. VI-1-3] shows the variation of peak as the time signal in our system. This peak is calculated
from the absolute of time signal.
[Fig. IV-1-3] The Peak Variation of Time Signal