RH PT12, Manual

Page: 31 / 48

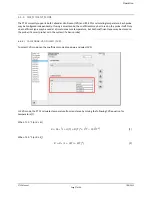
Operation
PT12 Manual 7/20/2021
Page 31 of 48
𝑊
𝑅
𝑅
[3]
ITS ‐ 90 defines two reference equations for an ideal probe. One equation defines resistance ratio,
𝑊
, as a function
of temperature in a range below the triple point of water, the other equation is for temperatures above the triple
point. Both reference equations are
𝑖
th
order polynomials defined as
𝑊
.
The reference equation below the triple point of water (where W
r
<1 and T <273.16K) is:
ln 𝑊 𝐴 𝐴
ln
𝑇
273.16 𝐾
1.5
1.5
[4]
While the reference equation above the triple point of water (where W
r
≥ 1 and T ≥ 273.16K) is:
𝑊 𝐶 𝐶
𝑇 754.15
481
[5]
Since the goal is to calculate temperature from resistance, both reference equations have inverses.
The inverse temperature reference equation below the triple point of water (where W
r
≥ 1 and T ≥ 273.16K) is:
𝑇 273.16 ∗ 𝐵 𝐵
𝑊
/
0.65
0.35
[6]
The inverse temperature reference equation above the tripe point of water (where W
r
≥ 1 and T ≥ 273.16K) is:
𝑇 𝐷 𝐷
𝑊 2.64
1.64
273.15
[7]
where
𝑇
is the temperature in Kelvin,
𝑊
is the reference resistance ratio, and
𝐴
and
𝐶
are constants given
in the ITS ‐ 90 standard. See the ITS ‐ 90 standard for a more complete definition, as well as the full table of constants
for
𝐴
,
𝐵
,
𝐶
, and
𝐷
.
No probe is ideal of course. Each exhibit small deviations that make their temperature vs. resistance characteristics
unique. To account for this, ITS ‐ 90 provides “deviation functions” for various temperature subranges, each with
their own equation and probe specific coefficients. These deviation functions provide unique probe correction to
the reference resistor ratio equation. The deviation functions utilized by the PT12 are listed below.
ITS ‐ 90 mode below triple point of water using A4 , B4 :
𝑊 𝑊 𝐴 4 𝑊 1 𝐵 4 𝑊 1 ∗ ln 𝑊
[8]
ITS ‐ 90 mode above triple point of water using A, B, C :
𝑊 𝑊 𝐴 𝑊 1 𝐵 𝑊 1 𝐶 𝑊 1
[9]
For the ITS ‐ 90 mode above the triple point of water, the coefficients for A, B, and C are:
A7 ‐ 11, B7 ‐ 11, and C7 ‐ 11.
Subrange 5 (SR5, spans triple point of water) using A5, B5 :
𝑊 𝑊 𝐴 5 𝑊 1 𝐵 5 𝑊 1
[10]