8. HOW TO USE THE INSTRUMENT ELBO CONTROLLI srl
Preset E236+
34
þ
Attention: it is possible to use all the measurement modes available to store the value of X and Z to print,
the only trickiness is to do it before the geometric calculus effect, otherwise the geometric drawing can’t
coincide with the profile of the tool.
In this case it is also possible to repeat several times the geometrical calculation, in order that E236+
recognizes all the required entities. Eventually proceed with short movement to exclude no relevant or
annoying profile parts for the achieved result.
For this type of analysis, tool profile cleaning and outline integrity is very important: the tools whose cutting
edge is splintered or excessively worn will not be recognized. Even lines or circles with profiles shorter
than 0.5 mm will not be recognized.
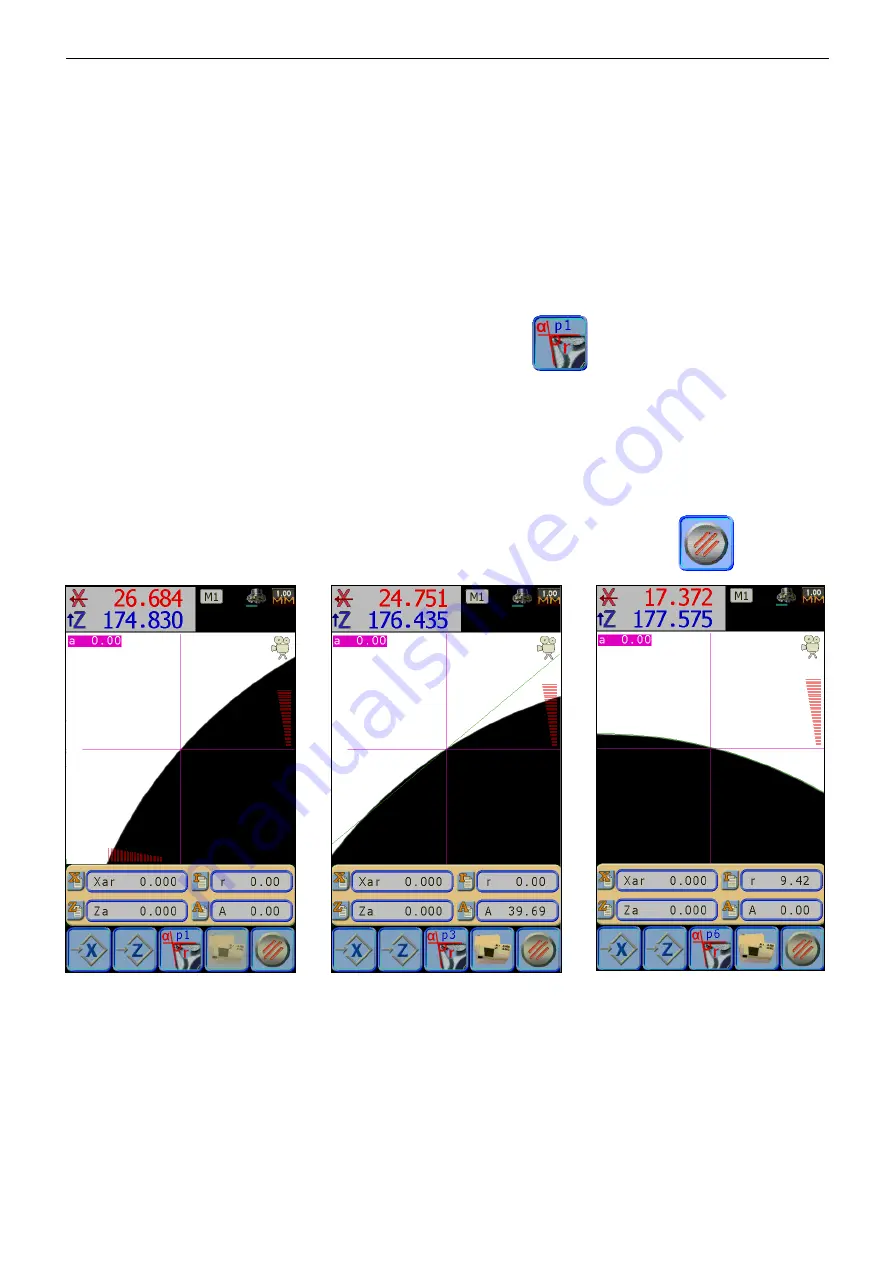
For each single point to be acquired, it will be necessary to move the axes along the tool profile, collimate
the shape with the centre of the fixed reticule, therefore push the
icon.
The icon on the button shows the number of the point to be stored. For each geometrical entity, it’s possible
to acquire up to 99 points: generally, the result will be more accurate using more points.
It’s necessary minimum 2 points to calculate the angle of a straight line, while it’s necessary, at least, 5
points to calculate the radius of a circumference.
At each new stored point, it’ll be carried out the calculus and it’ll be drawn the result on the screen. E236+
automatically recognizes if the stored points describe a straight line or a circumference, by adapting the
result.
Before to start a new calculus, delete the stored points sequence by pushing one time
icon.
þ
It’s normal that drawn the angle formed by first two points, also by measuring a radius, because they
fall on a straight line. The straight line will disappear by acquiring the points and it will be drawn a
circumference.
þ
In the event it’s necessary to print the result both radius and angle measured in manual mode, first of
all carry out the calculus of the radius.






























