Anfatec eLockIn 203, Manual

Page: 11 / 58

... (1 st , 2 nd , ... harmonic) are expected. For that reason the lock-in amplifier calculates
the following Fourier components S(m· ω
ref
) in the frequency domain from the input
signal s(t) in the time domain:
S

m
⋅
ref
 =
1

∫
−/
2
/
2
s

v

t
⋅
e
−
i m

ref
t
dt
. (2)
Together with equation (1) one receives the desired dependency of the measured signal
on the value of
v
0
at the frequencies
m·
ω
ref
:
S

m
⋅
ref
 =
∑
k
=
0
∞
s

k


v
0

v
1
k
k !
K
m
k
(3a)
with
K
m
k
=
1

∫
−/
2
/
2
cos
k

ref
t
⋅
e
−
i m

ref
t
dt . (3b)
Although the factors K
m
k
converge to zero for
k
to infinity, some factors remain
different from zero. Series elements of the n th order are also negligible if the
corresponding n th derivative of
s
(
v
0
) is negligible, too.
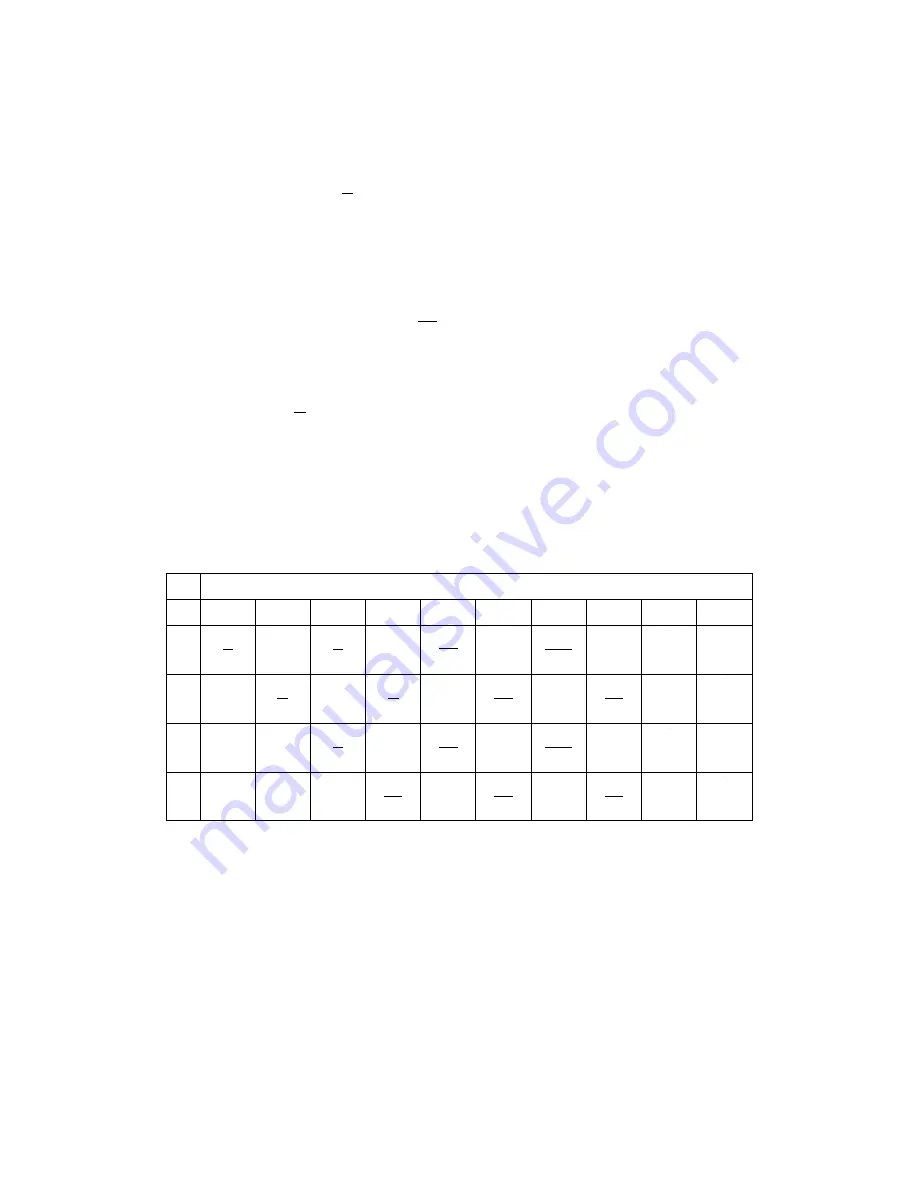
The factors
K
m
k
for the first four harmonics are shown in the table below:
k =
m 1 2 3 4 5 6 7 8 9 10
1
2
3
4
11 (58)
1
2 3
8 5
16
35
128
63
2 56
1
4 1
4 15
64 7
32
105
512
1
8 5
32
21
128
21
128
1
16
3
32
7
64
15
128