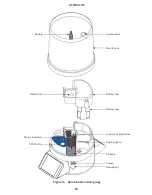
40
SYSTEM
For a given sound path length,
d
(m), the number of wavelengths,
n
, in still air is determined
with
Equation 5
.
Equation 5
n
=
vd
c
Here
v
is the frequency of the sound (Hz). When the air is moving, the speed of sound is the
sum of the wind speed and the speed of sound in still air. The anemometer transmits a sound
pulse in a forward direction, then a similar pulse in the reverse direction. The difference in
n
between the two points is computed. If the vector magnitude of the wind in the direction of
the sound is
u
(m/s), then
Equation 6
n
−Δ
n
+
=
vd
c
+
u
Equation 7
n
+ Δ
n
−
=
vd
c
−
u
for sound traveling with and against the wind. Subtracting the result of
Equation 6
from the
results of
Equation 7
creates
Equation 8
.
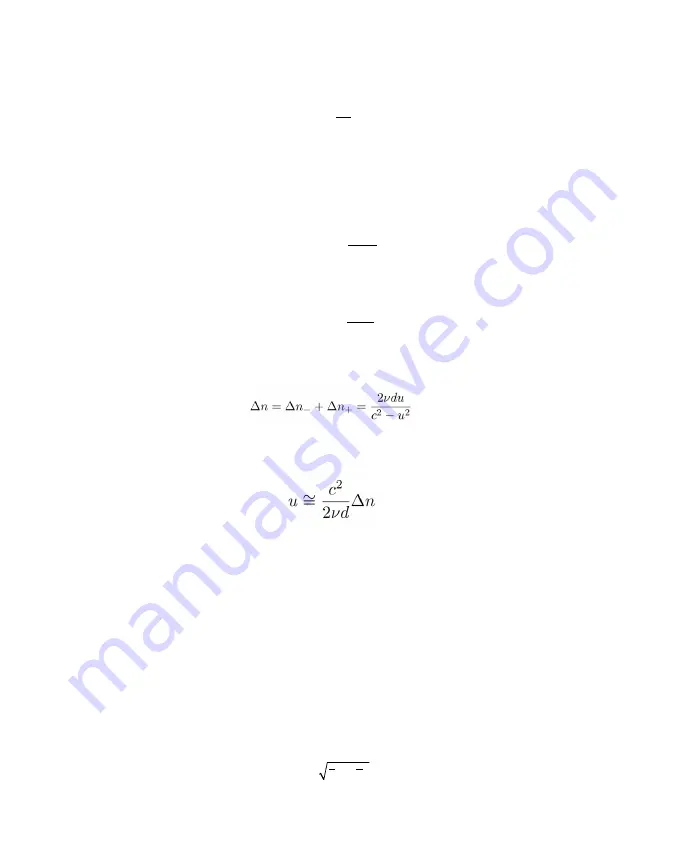
Equation 8
Even at the maximum wind speeds for the anemometer,
u
2 is only about 1% of
c
2, so the
equation can be simplified as shown in
Equation 9
.
Equation 9
This is the basic equation for the anemometer. Delta (∆) n is proportional to the phase
difference between the forward and reverse sound pulses. The sound comes from a
40 kHz ultrasonic transducer in the head of the anemometer. A sound pulse is transmitted
diagonally across the anemometer, bouncing off the convex plate. The sound pulse is then
received by another transducer in the anemometer head that is opposite the first. Once the
sound pulse is received, the receiver becomes the transmitter and the process is repeated.
Two more sensors, mounted at 90 degrees from the first two, give the other horizontal
component of the wind. The sound travels a total distance of about 72 mm from transmitter
to receiver, but
d
in the equations is just the horizontal distance, which is 40 mm.
If
u
is the magnitude of the wind vector in the east-west direction (east +), and
v
is the
magnitude in the north-south direction (north +), then the wind speed is computed
with
Equation 10
.
Equation 10
S
=
u
2
+
v
2