M-system SC100 Series, Applications Manual

Page: 64 / 103

64 SC100/200 Series Function Block Application Manual EM-6460-C
■
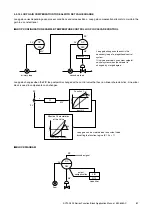
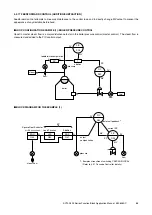
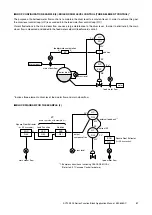
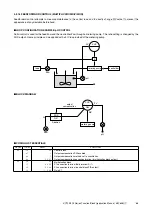
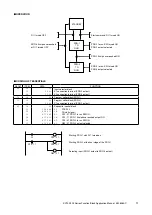
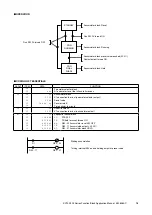
EXAMPLE (3): TEMPERATURE COMPENSATION FOR LIQUID DENSITY MEASUREMENT
User’s process function equation
γ
0
=
γ
t
+
α
( t
0
− t ) =
γ
t
−
α
t +
α
t
0
where
γ
0
: Compensated density (1.0 ... 1.3 kg/ l )
γ
t
: Uncompensated density (1.0 ... 1.3 kg/ l )
α
: Temperature compensation coefficient (0.0012 kg/ l )
t
0
: Reference temperature (50 °C)
t : Measured temperature (0 ... 100 °C)
Engineering unit function equation
Y
0
= Y
1
+ G
2
Y
2
+ B
0
..................................................................................................(Equation 12)
where
Y
0
= γ
0
Y
1
= γ
t
G
2
= − α
Y
2
=
t
B
0
= α
t
0
Engineering unit variables range
Y
0
= 1.0 ... 1.5
Y
1
= 1.0 ... 1.5
Y
2
= 0 ... 100
G
2
= -0.0012
B
0
= 0.0012 × 50 = 0.06
Normalized gains and biases (equations (4), (5) and (7))
K
1
= (1.5 − 1.0) / (1.5 − 1.0) = 1
K
2
= -0.0012 (100 − 0) / (1.5 − 1.0) = -0.24
A
0
= (1 − 0.0012 × 0 + 0.06 − 1 × 1) / (1.5 − 1.0) = 0.12
Normalization equation
X
0
= X
1
− 0.24X
2
+ 0.12 ...........................................................................................(Equation 13)
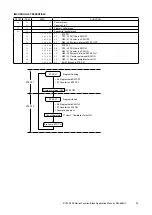
Confirming parameter ranges
Confirm that K
1
and K
2
are respectively within the range between -10.000 and +10.000. Confirm also that each
term in the equation does not overflow, remaining within the range between -3.2768 and +3.2767, when X
1
and
X
2
are equal to 1.
Recalculation
Normalization equation at X
1
= X
2
= 0.5 is given according to the equation (13):
X
0
= 0.5 − 0.24 × 0.5 + 0.12 = 0.5
Actual measurements at 50% are given respectively as:
Y
1
= 1.25
Y
2
= 50
Engineering unit function equation at 50% is given according to the equation (12):
Y
0
= 1.25 − 0.0012
×
50 + 0.06 = 1.25
Normalized Y
0
is given as X
0
= (1.25 − 1.0) / (1.5 − 1.0) = 0.5, corresponding to the result with the normalization
equation.