Harmonic Drive FHA-Cmini Series, Manual

Page: 64 / 68

Calculating inertia moment
Appendix
Apx-5
1
2
3
Apx
5
6
7
8
A
ppe
ndi
x
Apx
10
11
Apx
Apx
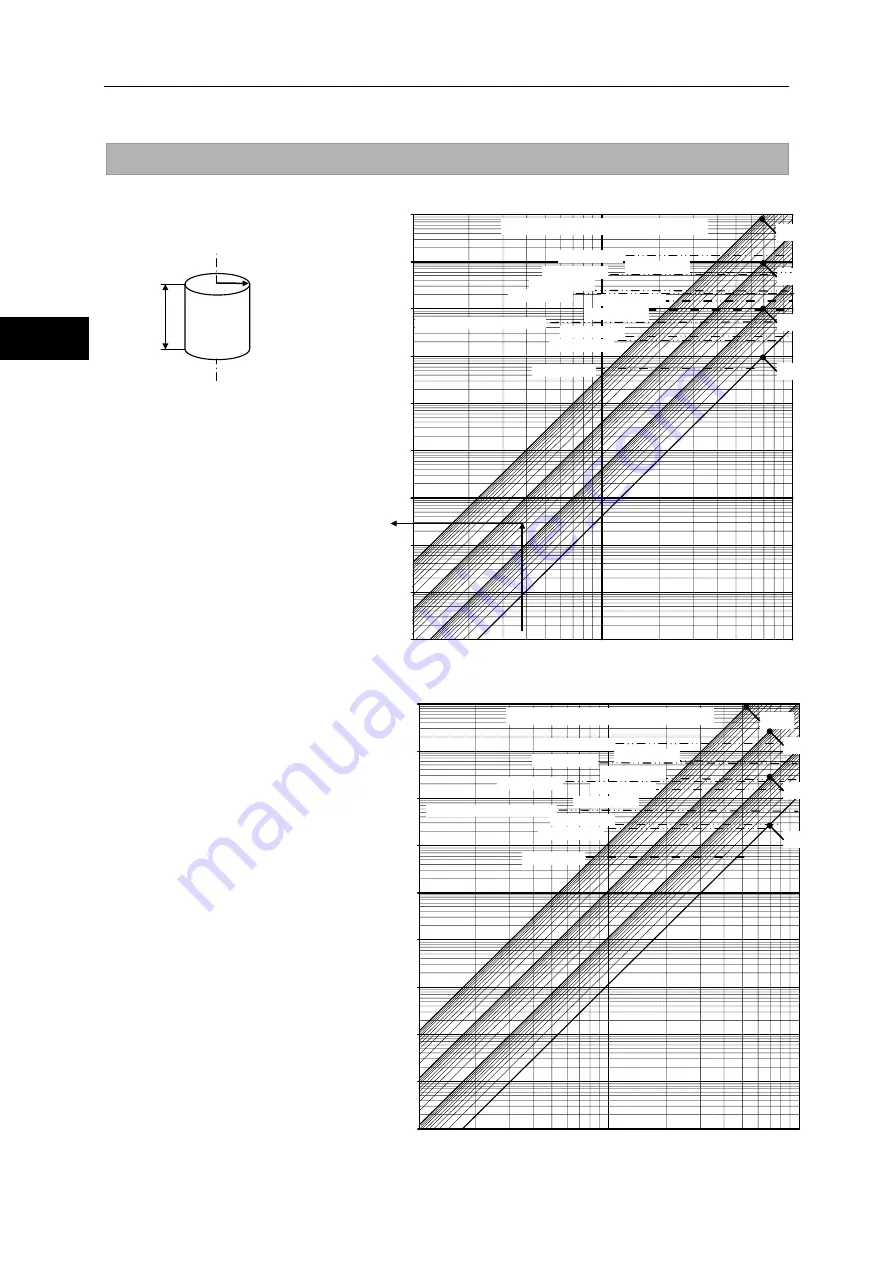
Inertia moment of a cylinder
The moment of inertia of a cylinder
may be obtained from the graphs to
the right.
Apply the top graph to aluminum
materials (specific gravity: 2.7) and
bottom graph to steel materials
(specific gravity: 7.85):
The double-dot dash lines in the
graph indicate the allowable
maximum inertia moment (estimated
value) for each FHA-C series
actuator.
(Example)
Material: Aluminum
Outer diameter: 100 mm
Length: 7 mm
Shape: Cylinder
Since the outer diameter is 100 mm,
the radius is 50 mm. Therefore, the
above graph gives the inertia
moment as
approx. 1.9 x 10-4 kg·m
2
.
(Calculated value: 0.000186 kg·m
2
)
Radius
Length
1000
100
10
1
0.1
0.01
0.001
10
-4
10
-5
10
-6
10 100 1000 20 30 50 70 200 300 500 700
Inertia moment (specific gravity: 2.7)
Inertia moment (kg·m
2
)
Radius R (mm)
Length (mm)
1000
100
10
1
FHA-17C-50
FHA-17C-100
FHA-25C-50
FHA-25C-100
FHA-40C-50
FHA-40C-100
FHA-17C-160, FHA-32C-50
FHA-25C-160
FHA-40C-160
FHA-32C-100
FHA-32C-160
1000
100
10
1
0.1
0.01
0.001
10
-4
10
-5
10
-6
10 100 1000 20 30 50 70 200 300 500 700
Inertia moment (specific gravity: 7.85)
1000
100
10
1
FHA-17C-50
FHA-17C-100
FHA-25C-50
FHA-25C-100
FHA-40C-50
FHA-40C-100
FHA-17C-160, FHA-32C-50
FHA-25C-160
FHA-40C-160
FHA-32C-100
FHA-32C-160
Inertia moment (kg·m
2
)
Radius R (mm)
Length (mm)