manualshive.com logo in svg

Thytronic Pro-N NVA100X-D, Руководство пользователя

Поделиться
Скачать
Thytronic Pro-N NVA100X-D Скачать руководство пользователя страница 48

48

NVA100X-D - Manual - 02 - 2016

FUNCTION CHARACTERISTICS

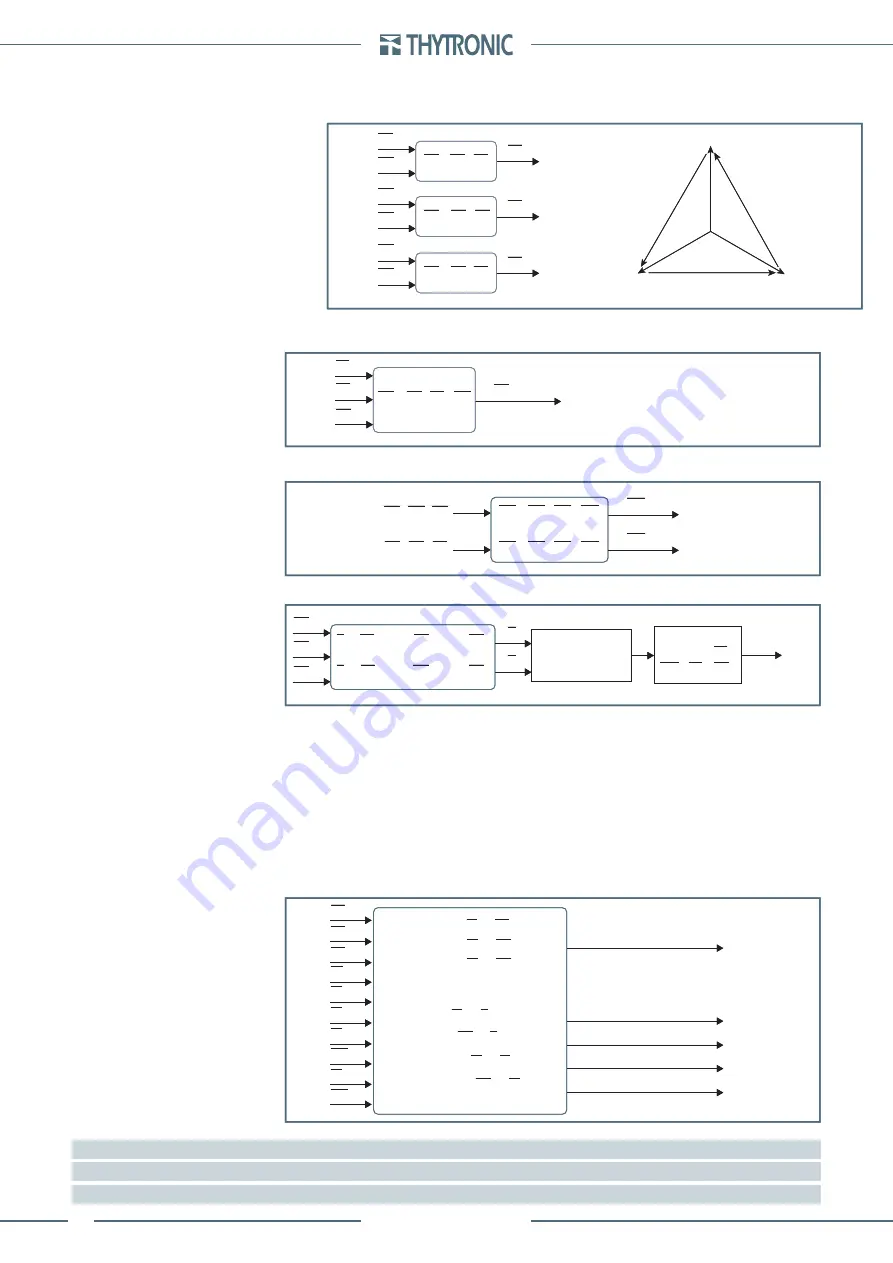
By means vector addition of direct measures the following are calculated (RMS value of fundamen-

tal components):

Phase-to-phase voltages: 

U

12

, 

U

23

, 

U

31

Fundamental component of the calculated residual voltage 

U

EC

[1]

Fundamental component of the calculated residual currents 

I

ECH

 and 

I

ECL 

[2]

Thermal image Δ

θ

Phase

[3]

Displacement angle of any phase current respect the corresponding phase-to-neutral voltage: 

Phi

L1

, 

Phi

L2

, 

Phi

L3

, 

Displacement angle of the measured residual current respect the measured residual voltage (posi-
tive with current in lagging direction in respect to voltage): 

Phi

E

,

Displacement angle of the measured residual current respect the calculated residual voltage (pos-
itive with current in lagging direction in respect to voltage): 

Phi

EC

Displacement angle of the calculated residual current respect the measured residual voltage (pos-
itive with current in lagging direction in respect to voltage): 

Phi

E_IEC

Displacement angle of the calculated residual current respect the calculated residual voltage 
(positive with current in lagging direction in respect to voltage): 

Phi

EC_IEC

Note 1  The residual voltage is available as a direct measure U

E 

and computed measure U

EC

,

Note 2  The residual currents are available with either direct measurement (IE1 and IE2) and as calculated measure  

(

I

ECH

 and I

ECL

)

Note 3  The adjustment and display range of displacements are 0°... 359°

•

•

•

•

•

•

•

•

•

U 1 2 . a i

U

L1

U

12

 = 

U

L1 

- 

U

L2

U

12

U

23

U

31

U

23

 = 

U

L2 

- 

U

L3

U

31

 = 

U

L3 

- 

U

L1

U

L2

U

L2

U

L3

U

L1

U

L3

(

U

n

)

(

U

n

)

(

U

n

)

U

L1

U

12

U

31

U

23

U

L3

U

L2

U 1 2 . a i

U

L1

U

12

 = 

U

L1 

- 

U

L2

U

12

U

23

U

31

U

23

 = 

U

L2 

- 

U

L3

U

31

 = 

U

L3 

- 

U

L1

U

L2

U

L2

U

L3

U

L1

U

L3

(

U

n

)

(

U

n

)

(

U

n

)

U

L1

U

12

U

31

U

23

U

L3

U

L2

U E C . a i

U

L1

U

EC

 = 

U

L1 

+ 

U

L2 

+ 

U

L3

U

EC

U

L3

U

L2

(

U

En

)

U E C . a i

U

L1

U

EC

 = 

U

L1 

+ 

U

L2 

+ 

U

L3

U

EC

U

L3

U

L2

(

U

En

)

I E C . a i

I

ECH

 = 

I

L1H 

+ 

I

L2H 

+ 

I

L3H

I

ECH

I

ECH

 = 

I

L1H 

+ 

I

L2H 

+ 

I

L3H

(

I

nH

)

I

ECL

(

I

nL

)

I

L1H

,

I

L2H

,

I

L3H

I

L1L

,

I

L2

L

,

I

L3

L

I E C . a i

I

ECH

 = 

I

L1H 

+ 

I

L2H 

+ 

I

L3H

I

ECH

I

ECH

 = 

I

L1H 

+ 

I

L2H 

+ 

I

L3H

(

I

nH

)

I

ECL

(

I

nL

)

I

L1H

,

I

L2H

,

I

L3H

I

L1L

,

I

L2

L

,

I

L3

L

T h e t a . a i

I

L1L

I

2

I

2

 = (

I

L1L

+ e

-j120°

I

L 2 L

+ e

+j120°

I

L 3 L

)

I

1

 = (

I

L1L

+ e

+j120°

I

L 2 L

+ e

-j120°

I

L 3 L

)

I

L3L

I

L2L

I

1

I

t h

 = √(

I

1

2

+

K

2

2

∙

I

2

2

)

Δ

θ

(Δ

θ

B

)

2

dΔ

θ

dt

I

B

I

t h

Δ

θ

T+

T+

(   )

+

=

T h e t a . a i

I

L1L

I

2

I

2

 = (

I

L1L

+ e

-j120°

I

L 2 L

+ e

+j120°

I

L 3 L

)

I

1

 = (

I

L1L

+ e

+j120°

I

L 2 L

+ e

-j120°

I

L 3 L

)

I

L3L

I

L2L

I

1

I

t h

 = √(

I

1

2

+

K

2

2

∙

I

2

2

)

Δ

θ

(Δ

θ

B

)

2

dΔ

θ

dt

I

B

I

t h

Δ

θ

T+

T+

(   )

+

=

F a s e . a i

ϕ

L1

 = 



I

L1 

-



U

L1

Phi

L1

, 

Phi

L 2

,

Phi

L 3

Phi

E

Phi

EC

(

°

)

(

°

)

(

°

)

U

L1

ϕ

L 2

 = 



I

L 2 

-



U

L 2

ϕ

L 3

 = 



I

L 3 

-



U

L 3

ϕ

E

 = 



U

E  

-



I

E

ϕ

EC

 = 



U

EC 

-



I

E

Phi

E_IEC

Phi

EC_IEC

(

°

)

(

°

)

ϕ

E_IEC

 = 



U

E  

-



I

EC

ϕ

EC_IEC

 = 



U

EC  

-



I

EC

U

L2

U

L2

I

L1L

I

L2L

I

L3L

U

E

U

EC

I

EC

I

E

F a s e . a i

ϕ

L1

 = 



I

L1 

-



U

L1

Phi

L1

, 

Phi

L 2

,

Phi

L 3

Phi

E

Phi

EC

(

°

)

(

°

)

(

°

)

U

L1

ϕ

L 2

 = 



I

L 2 

-



U

L 2

ϕ

L 3

 = 



I

L 3 

-



U

L 3

ϕ

E

 = 



U

E  

-



I

E

ϕ

EC

 = 



U

EC 

-



I

E

Phi

E_IEC

Phi

EC_IEC

(

°

)

(

°

)

ϕ

E_IEC

 = 



U

E  

-



I

EC

ϕ

EC_IEC

 = 



U

EC  

-



I

EC

U

L2

U

L2

I

L1L

I

L2L

I

L3L

U

E

U

EC

I

EC

I

E

Содержание Pro-N NVA100X-D

Страница 1: ...NVA100X D Manual 02 2016 MANUAL NVA100X D THE COMPREHENSIVE SOLUTION FOR DIFFERENTIAL PROTECTION OF GENERATORS MOTORS TRANSFORMERS...

Страница 2: ...ide 1 and side 2 15 Phase voltage inputs 15 Residual voltage input 15 Binary inputs 15 Block input Logic selectivity 15 3 3 OUTPUT CIRCUITS 16 Relays 16 Block output Logic selectivity 16 3 4 MMI Man M...

Страница 3: ...rip Circuit Supervision 74TCS 38 Selective block BLOCK2 38 Internal selective block BLOCK4 38 Circuit Breaker supervision 38 VT supervision 74VT 38 CT supervision 74CT side H 38 CT supervision 74CT si...

Страница 4: ...block BLOCK4 255 Logical block summary 258 Remote tripping 260 Frequency tracking 261 Second Harmonic Restraint 2ndh REST 262 Cold Load Pickup CLP 263 Cold Load Pickup CLP for motor generator protect...

Страница 5: ...ve ANSI IEEE type VI 343 Negative sequence overcurrent 46M Extremely inverse time curve ANSI IEEE type EI 344 Phase overcurrent 50 51 side H and side L Moderately inverse time curve ANSI IEEE type MI...

Страница 6: ...id to the following symbols Installation and commissioning must be carried out by quali ed person Thytronic assumes no re sponsibility for damages caused from improper use that does not comply all war...

Страница 7: ...ions fn Rated frequency InH Relay phase rated current side H InpH Phase CT primary rated current side H InL Relay phase rated current side L InpL Phase CT primary rated current side L Ing Protected de...

Страница 8: ...polarity mark of CTs as an alternative to a ANSI no dot S1 IEC nomenclature for secondary polarity mark of CTs as an alternative to a ANSI dot S2 IEC nomenclature for secondary polarity mark of CTs as...

Страница 9: ...to the 2nd threshold of the 50 element It is not available for reading missing arrow AND and NAND logic gates OR and NOR logic gates Limit block I threshold Computation block Max phase current Thresho...

Страница 10: ...FF tOFF Minimum pulse width operation for output relays tTR tTR t tTR INPUT OUTPUT tTR 0 T tTR t tTR INPUT OUTPUT Latched operating mode for output relays and LEDs Pulse operating mode for output rela...

Страница 11: ...ettings Two residual current side 1 and side 2 with rated currents independently selectable at 1 A or 5 A by means of sw settings Three phase voltages line to ground with rated voltages programmable i...

Страница 12: ...ange and a very small power dissipation Nominal frequency 50 or 60 Hz The most signi cant operating features are Programming of operating modes and parameters by means of the front keys and alphanumer...

Страница 13: ...erruptions and voltage variations on dc input power port immunity tests Interruption UT 40 100 ms Interruption UT 0 50 ms Voltage variations UT 80 120 10 s EMC tests for interference immunity Referenc...

Страница 14: ...tory magnetic eld Damped oscillatory wave 0 1 MHz 30 A m Damped oscillatory wave 1 MHz 30 A m Emission Reference standards EN 60255 25 IEC 60255 25 EN 61000 6 4 IEC 61000 6 4 EN 55011 CISPR 11 Electro...

Страница 15: ...ordip switch Permanent overload 25 A Thermal overload 1 s 500 A Dynamic overload half cycle 1250 A Rated consumption 0 006 VA with IEn 1 A 0 12 VA with IEn 5 A Phase voltage inputs Relay phase to phas...

Страница 16: ...Ethernet 100 Base TX Baud rate 230400 bps Protocol ModBus TCP IP Connector RJ45 Remote ports RS485 Connection screw terminals Baud rate 1200 57600 bps Protocol 2 ModBus RTU IEC 60870 5 103 DNP3 Ether...

Страница 17: ...tep 1 A 500 4990 A step 10 A 5000 20000 A step 100 A Primary nominal current chosen as reference Inref 3 set by device Side reference for compensation Refsize 2 set by device Current matching type Mat...

Страница 18: ...CTIVE FUNCTIONS Base current IB Base current IB 1 0 10 2 50 In step 0 01 In Underimpedance 21 Z Element De nite time First threshold de nite time Z def 0 02 3 00 Zn 2 step 0 01 Zn Operate time tZdef 0...

Страница 19: ...Operate time accuracy 5 or 10 ms Positive sequence undervoltage 27V1 U1 Element De nite time First threshold de nite time U1 def 0 05 1 10 En step0 01En Operating time tU1 def 0 07 100 0 s 0 07 9 99...

Страница 20: ...ing direction P1 DIR PForward PReverse PForward Reverse De nite time First threshold de nite time P1 def 0 01 1 50 Pn Operating time tP1 def 0 07 100 0 s 0 07 9 99 s step 0 01 s 10 0 100 0 s step 0 1...

Страница 21: ...Maximum operating time t2MAX 500 2000 s step 1 s Pickup time 0 04 s Dropout ratio 0 95 0 98 Dropout time 0 05 s Overshoot time 0 04 s Pickup accuracy 1 with I2 0 5 In Operate time accuracy 5 or 10 ms...

Страница 22: ...1 min Cooling time constant T 1 0 6 0 step 0 1 CLP operating mode DthCLP Mode OFF Blocking Change setting CLP activation time tDthCLP 0 00 200 s 0 00 9 99 s step 0 01 s 10 0 99 9 s step 0 1 s 100 200...

Страница 23: ...00 100 0 s 0 00 9 99 s step 0 01 s 10 0 100 0 s step 0 1 s Reset time delay t H RES 0 00 100 0 s 0 00 9 99 s step 0 01 s 10 0 100 0 s step 0 1 s De nite time Second threshold de nite time I H def 0 1...

Страница 24: ...me delay t L RES 0 00 100 0 s 0 00 9 99 s step 0 01 s 10 0 100 0 s step 0 1 s De nite time First threshold de nite time I L def 0 100 40 0 InL 0 100 0 999 In step 0 001 InL 1 00 9 99 In step 0 01 InL...

Страница 25: ...s step 0 01 s I L Element CLP operating mode I L CLP Mode OFF ON Element blocking ON Change setting CLP activation time t L CLP 0 00 100 0 s 0 00 9 99 s step 0 01 s 10 0 100 0 s step 0 1 s Reset time...

Страница 26: ...U def Operating time t I U def 0 07 100 0 s 0 07 9 99 s step 0 01 s 10 0 100 0 s step 0 1 s I I U Element I I U Reset time delay t I U RES 0 00 100 0 s 0 00 9 99 s step 0 01 s 10 0 100 0 s step 0 1 s...

Страница 27: ...1 s IE1 Reset time delay tE1 RES 0 00 100 0 s 0 00 9 99 s step 0 01 s 10 0 100 0 s step 0 1 s De nite time 50N 1 51N 1 Third threshold de nite time IE1 def 0 002 10 00 IEn1 0 002 0 999 IEn1 step 0 00...

Страница 28: ...1 s 10 0 100 0 s step 0 1 s De nite time 50N 2 51N 2 Second threshold de nite time IE2 def 0 002 10 00 IEn2 0 002 0 999 IEn2 step 0 001 IEn2 1 00 10 00 IEn2 step 0 01 IEn2 IE2 def within CLP IE2CLP de...

Страница 29: ...In 1 00 20 00 In step 0 01 In IEC inv within CLP IECCLP inv 0 100 20 00 In 0 100 0 999 IE step 0 001 In 1 00 20 00 In step 0 01 In IEC inv Operating time tEC inv 0 02 60 0 s 0 02 9 99 s step 0 01 s 1...

Страница 30: ...points CPhi1 Tripping direction CPhi1 DIR CosPhi Lag CosPhi Lead CosPhi Lag Lead De nite time 55 First threshold de nite time CPhi1 def 0 10 0 99 step 0 01 CPhi1 def Operating time tCPhi1 def 0 04 100...

Страница 31: ...time 59N First threshold inverse time UE inv 0 01 0 50 UEn step 0 01 UEn UE inv Operating time tUE inv 0 10 100 0 s 0 10 9 99 s step 0 01 s 10 0 100 0 s step 0 1 s UE Element UE Reset time delay tUE...

Страница 32: ...2 Residual voltage pickup value 0 004 0 500 UEn step0 001UEn Characteristic angle 0 359 step 1 Half operating sector 1 180 step 1 IED def within CLP IEDCLP def 0 002 10 00 IEn2 0 002 0 999 IEn2 step 0...

Страница 33: ...0 s 0 02 9 99 s step 0 01 s 10 0 60 0 s step 0 1 s IED Element CLP operating mode IEDCLP Mode OFF ON Element blocking ON Change setting CLP activation time tEDCLP 0 00 100 0 s 0 00 9 99 s step 0 01 s...

Страница 34: ...5 or 10 ms Directional earth fault overcurrent with calculated residual current 67N Comp Common con guration 67N Comp Operating mode Mode67NC I I cos Residual voltage measurement type for 67NC direct...

Страница 35: ...Half operating sector 1 180 step 1 Note 1 All the formulas for IECH residual current calculated on side H the same for IECL residual current calculated on side L Standard Inverse Time IEC 255 3 BS142...

Страница 36: ...OFF ON Element blocking ON Change setting CLP activation time tEDCCLP 0 00 100 0 s 0 00 9 99 s step 0 01 s 10 0 100 0 s step 0 1 s IEDC Reset time delay tEDC RES 0 00 100 0 s 0 00 9 99 s step 0 01 s 1...

Страница 37: ...rmonic restraint 87T 87T Second harmonic restraint threshold 2nd REST 10 80 Id step 1 Id 87T Fifth harmonic restraint threshold 5th REST 10 80 Id step 1 Id 87T Harmonic restraint intentional reset tim...

Страница 38: ...ut time for ground protections tFI IE 0 00 10 00 s step 0 01 s Circuit Breaker supervision Circuit breaker diagnostic Number of CB trips threshold N Open 0 10000 step 1 Cumulative CB tripping currents...

Страница 39: ...igger time 0 05 1 00 s step 0 01 s Post trigger time 0 05 60 00 s step 0 05 s Set sample channels iL1 H iL2 H iL3 H iL1 L iL2 L iL3 L iE1 iE2 uL1 uL2 uL3 uE iL1cH iL2cH iL3cH iL1cL iL2cL iL3cL iSL1 iS...

Страница 40: ...of fundamental component for phase voltages UL1 UL2 UL3 RMS value of fundamental com for residual current side 1 IE1 RMS value of fundamental com for residual current side 2 IE2 RMS value of fundament...

Страница 41: ...Max of the 2nd harmonic phase currents Fundamental component percentage ratio I 2nd IL I 2nd IL Third harmonic of phase currents IL1 3rd IL2 3rd IL3 3rd Third harmonic of residual current IE 3rd Third...

Страница 42: ...contains all the circuits necessary for performing the analogue and digital pro cessing of the signals hw ai RTC EEprom Flash Thybus RS485 RS232 Ethernet SRam CPU ETHERNET CPU INPUT MODULE CTs VTs OUT...

Страница 43: ...The following are envisaged Real Time Clock circuits with oscillator and super capacitor RS232 communication port RS485 communication port Thybus communication circuits for external modules and MMI b...

Страница 44: ...l BP Task The task process e thread are the base components Example are Keyboard management RTC Real Time Clock updating RAM EEPROM updating Diagnostic Input acquisition Output relay management MMI I...

Страница 45: ...Basic Protocol BP manages the service communication between the kernel and the other modules through the communication buses with the following services Data and information exchange Calibration Upgr...

Страница 46: ...sures second level Derived third level The measures concerning a level are based on data worked out in the previous level For each level the required resources concerning the priority for tasks condit...

Страница 47: ...InH InL iL1H iL2H iL3H iL1L iL2L iL3L DFT IL1H IL2H IL3H IL1L IL2L IL3L ACQUISITION IL1 ai InH InL iL1H iL2H iL3H iL1L iL2L iL3L DFT IL1H IL2H IL3H IL1L IL2L IL3L ACQUISITION uL1 uL2 uL3 DFT UL1 UL2...

Страница 48: ...able as a direct measure UE and computed measure UEC Note 2 The residual currents are available with either direct measurement IE1 and IE2 and as calculated measure IECH and IECL Note 3 The adjustment...

Страница 49: ...2 2 un U2 ai UL1 U1 U2 U2 UL1 e j120 UL2 e j120 UL3 3 U1 UL1 e j120 UL2 e j120 UL3 3 UL3 UL2 e j120 3 j 1 2 2 e j120 3 j 1 2 2 un Fix Demand ai 1s IL1FIX IL2FIX IL3FIX PFIX tFIX P Q In Pn Qn QFIX IL2...

Страница 50: ...tervaltROL Average inside time intervaltROL Min Demand ai Reset IL1MIN IL2MIN IL3MIN PMIN P Q In Pn Qn QMIN IL2L IL1L IL3L 1s tROL tROL tROL tROL tROL tROL MIN ILxMIN ILxn tROL 60 tR OL 60 n 1 1 MIN P...

Страница 51: ...ond refresh EA Positive and negative reactive energy one second refresh EQ EQ Total reactive energy one second refresh EQ Use of over described measures is shown in the following tables E ai EA Pdt EA...

Страница 52: ...IL3L IL1L IL2L IL3L IL2L IL1L IL1L IL2L IL3L IL1L IL2L IL3L IL2L IL3L IL1L IL2L IL1L IL3L IL3L IL2L IL1L IL3L IL1L IL2L Direct sequence cyclic order for side H currents Base Direct sequence cyclic or...

Страница 53: ...rator Transformer side H CTs Polarity NORMAL Polarity NORMAL Polarity NORMAL Polarity NORMAL C1 C3 C5 C7 terminals C2 C4 C6 C8 terminals A1 A3 A5 A7 terminals A2 A4 A6 A8 terminals C1 C3 C5 C7 termina...

Страница 54: ...D Resistive inductive load convenzioni ai Resistive inductive load SYSTEM Q QL1 QL2 QL3 cos cos L1 cos L2 cos L3 cos cos L1 cos L2 cos L3 cos cos L1 cos L2 cos L3 cos cos L1 cos L2 cos L3 Q QL1 QL2 QL...

Страница 55: ...1 cos L2 cos L3 Q QL1 QL2 QL3 I II IV III P PL1 PL2 PL3 P PL1 PL2 PL3 S SL1 SL2 SL3 UL1 IL2 IL3 IL1 UL2 UL3 SYSTEM SYSTEM B3 B5 B7 NVA100X D A1 A3 A5 Resistive capacitive load Resistive capacitive loa...

Страница 56: ...ervoltage 59N g g g g g g g g Negative sequence overvoltage 59V2 g Low impedance restricted earth fault 64REF g g g g g g g g g g g g Directional earth fault overcurrent 67N g g g g g g g g g g g g Di...

Страница 57: ...e elements g g g g g g Block2 IE selective block from ground elements g g g g g g Block1 logic block side H L g g g g g g Block1 logic block side H g g g g g g Block1 logic block side L g g g g g g Bl...

Страница 58: ...time of motor is cleared Total counter g g g g g g Reset LEDs If the element tripped have gone back to rest condition the latched LEDs and or relays may be reset Set pro le Inside Pro N devices two i...

Страница 59: ...application of the inputs for the acquisition of Block2 selective block for Phase Block2 Iph and earth protective functions Block2 IE is similar to that illustrated in the scheme concerning the Block2...

Страница 60: ...blocked from Block1 Note 2 The reset of the total counters is practicable by means ThySetter command with Session Level 1 available with password Block1 ai xxxx Block1 Enable ON Enable Block1 input O...

Страница 61: ...input INx T 0 IN2 tON T 0 n o n c INx tON Logic INx tOFF IN2 tOFF Binary input allocation for CB remote command TRIPPING M ATRIX LED REL AYS UAUX UAUX 52a 52 O I 52b CB com ai OPEN Command CLOSE Comm...

Страница 62: ...ures I L Bk Logic block of I ele ment The input activation make a block of the I side L element through virtual I O I L Bk Logic block of I ele ment The input activation make a block of the I side L e...

Страница 63: ...tOFF INx tOFF Speed switch M 3 51LR Speed switch Speed control UAUX UAUX Speed control Binary input INx INx T 0 INx tON T 0 n o n c INx tON Logic INx tOFF INx tOFF Speed switch M 3 51LR Timers restart...

Страница 64: ...le timer is matched minimum pulse width operation When latched operating mode is set Operation MODE Latched the output relay doesn t reset at the end of the trip condition it stays ON until a reset co...

Страница 65: ...arm element relays DthMGAL1 K g g g g g g 49MG Second element alarm relays DthMGAL2 K g g g g g g 49MG Element trip relays DthMG K g g g g g g 50 51 First element start relays I ST K g g g g g g 50 51...

Страница 66: ...g g g g 81O Second element trip relays f TR K g g g g g g 81U First element start relays f ST K g g g g g g 81U First element trip relays f TR K g g g g g g 81U Second element start relays f ST K g g...

Страница 67: ...Latched the LED doesn t reset at the end of the trip condition it stays ON until a manual reset com mand is issued RESET key ThySetter or communication command Any change to the settings can be affect...

Страница 68: ...ement Trip LEDs DthMGAL2 L g g g g g g g g g g 49MG First alarm element Trip LEDs DthMG L g g g g g g g g g g 50 51 First element Start LEDs I ST L g g g g g g g g g g 50 51 First element Trip LEDs I...

Страница 69: ...1O Second element Trip LEDs f TR L g g g g g g g g g g 81U First element Start LEDs f ST L g g g g g g g g g g 81U First element Trip LEDs f TR L g g g g g g g g g g 81U Second element Start LEDs f ST...

Страница 70: ...orts module optical ber network with multiplexed operation mode Two FX ports module optical ber network RSTP 4 Modbus TCP basically embeds a Modbus frame into a TCP frame in a simple manner This is a...

Страница 71: ...NT internal EXT external CTs Protected object ProtObj Setting the type of protecting object xed to TRANSF Relay residual current side 1 and side 2 IEn1 and IEn2 This rated values must be set by means...

Страница 72: ...be estimated by means of the general formula UEn 3 Ung KVT 3 6900 3 100 69 V Example A2 Es2 Un ai KVT V V 6000 3 100 3 60 V V 6000 3 100 3 60 Grid rated voltage Ung 6 kV VTs ratio KVT Ung Uns Ung 6 k...

Страница 73: ...UECn is estimated automatically by means of the formula UECn Un 3 100 3 173 V VT ratio KVT Grid nominal voltage Ung where the VTs V 3 are connected UEn VT ratio KVT Grid nominal voltage Ung where the...

Страница 74: ...ected It must be programmed to the same value of the residual CT s primary nominal current Example 1 The residual CT primary current IEn1p and IEn2p must be set as IEn1p IEn2p 100 A Example 2 The resi...

Страница 75: ...ust be adjusted to UEnp 3 Ung 3 6900 V 11900 V Grid rated voltage Ung 6 9 kV VTs ratio KTV Relay rated voltage Un 69 V Es1 Ung ai KTV V V 10000 3 100 3 100 V V 10000 3 100 3 100 Un 69 V Ung 6 9 kV 52...

Страница 76: ...rounding side H GndH Transformer connection side H ConnH Transformer vector group side H VectGroupH Transformer nominal voltage side L VntL Transformer nominal current side L IntL 3 Transformer mismat...

Страница 77: ...equired to sustain the permanent current may be some multiple of rated current ie 2 4 In From the generator synchronous reactance Xd Even with excitation system capable of forcing the short circuit cu...

Страница 78: ...a possible inhibition on stage has no effect on the rest t int F21 ai Z Z Z tZ t tZ TRIP General operation time characteristic curve for the underimpedance element 21 t int F21 ai Z Z Z tZ t tZ TRIP...

Страница 79: ...wire link is active Use of committed pilot wire input BLIN1 The protection is blocked off according the selectivity block criteria when the input BLIN1 is active The information about phase or phase...

Страница 80: ...on element BLK2OUT Iph IE whenever the given ele ment Start I H Start I H e o Start I H becomes active The enable Z BLK2OUT and or Z BLK2OUT parameters ON or OFF are available inside the Set Pro le A...

Страница 81: ...tF IE Z Block2 OUT Z Block2 OUT Iph block2 output Iph IE block2 output IE block2 output Z Start IPh Block2 input IPh Block2 IE Block2 input Block2 IN diagnostic Block2 output Block2 input FROM EARTH F...

Страница 82: ...Start Block2 IN diagnostic Iph IE block2 output T 0 tF all T 0 tF Iph T 0 tF IE Z Block2 OUT Z Block2 OUT Z Block2 OUT Iph block2 output Iph IE block2 output IE block2 output Z Start IPh Block2 input...

Страница 83: ...arings with the aim of detecting localised overheating due to worn or non lubricated bearings The Pt100 probes detect the temperature in the range 50 C 250 C at 0 C its resistance is 100 ohm an alarm...

Страница 84: ...mpensated resistance connections resulting in an error proportional to the value of introduced resistance The connection to the probes must be made with three conductors shielded cables and the screen...

Страница 85: ...erate time setting For the inverse time characteristic following data applies The operate time setting is referred to an input voltage equal to 1 4 of the pickup value Asymptotic reference value minim...

Страница 86: ...when the input block goes down 3 The enabling parameters are available inside the Set Pro le A or B Undervoltage 27 U Element U Element Setpoints menus while the Block1 function must be assigned to t...

Страница 87: ...undervoltage element U Enable ON Inhibit Disable 27 function by operator Logic diagram concerning the rst threshold U of the undervoltage element 27 Fun F27_S2 ai Block 74VT VT fault 74VT 0 without fa...

Страница 88: ...1 10 100 1000 10000 t s 0 25 tU inv 100 s tU inv 10 s tU inv 0 1 s tU inv 1 s t tU inv 1 U U inv 0 75 F_27 Char ai Inverse time operating characteristic concerning the rst threshold U of the undervolt...

Страница 89: ...s set to ON The parameters are available inside the Set Pro le A or B Positive sequence undervoltage 27V1 U1 Element Setpoints menu 1 VT supervision 74VT The element may be blocked whenever the VT sup...

Страница 90: ...U1 def 0 T TRIPPING M ATRIX LED REL AYS tU1 def Start U1 U1 ST K Start U1 U1 TR K U1 ST L U1 TR L Trip U1 Trip U1 Trip U1 BF Enable ON Enable U1 BF towards BF logic BLK1U1 U1 BF Enable ON Enable Block...

Страница 91: ...Reverse P1 Tripping direction P Forwaed Reverse P Q TRIP P1 P1 Tripping direction P Forward General operation time characteristic for the directional active overpower element 32P P Q TRIP P1 P1 Trippi...

Страница 92: ...t can produce the Breaker Failure output if the P1 BF P2 BF parameters are set to ON The parameters are available inside the Set Pro le A or B Directional active overpower 32P P1 Element P2 Element Se...

Страница 93: ...0 n o n c INx tOFF P2 DIR P2 def tP2 def tP2 RES T 0 tP2 RES Directional active overpower 32P Second element logic diagram P2 Fun_32 P1 ai P P1 def P1 Start P1 Start P1 Trip P1 Trip RESET tP1 def 0 T...

Страница 94: ...e command is ended The following block criteria is available Logical block Block1 If the I BLK1 enabling parameter are set to ON and a binary input is designed for logical block Block1 the protection...

Страница 95: ...t 37 Fun F37_S1 ai RESET t def 0 T TRIPPING M ATRIX LED REL AYS t def Start I I ST K Start I I TR K I ST L I TR L Trip I Trip I BLK1I Enable ON Enable Block1 input ON Block I BLK1 Block1 Block1 Logic3...

Страница 96: ...put relay U and or U thresholds are forced to reset state the message Disabled 27 27V1 37P 37Q is displayed and all LEDs blink until the end of the command P1 Tripping direction P Forward P1 Tripping...

Страница 97: ...er 74VT BK EN and 74CT BK EN are available inside the Set VT supervision 74VT and Set CT supervision 74CT menus Logical block Block1 If the P1 BLK1 and or P1 BLK1 enabling parameters is set to ON and...

Страница 98: ...f P P1 DIR P1 def ON Inhibit Disable 27 function by operator Directional active underpower 37P First element logic diagram P1 Fun F37P_S2 ai RESET tP2 def 0 T TRIPPING M ATRIX LED REL AYS P2 Start P2...

Страница 99: ...to avoid the risk of tripping during stable power swings resulting from the elimination of grid faults or the synchronisation of the machine Instead when the loss of excitation occurs with a high init...

Страница 100: ...tions concerning the alarm element are lled and the RL1 and XL1 computed values are placed inside the circle with equation RL1 2 XL1 XC1 2 XD1 2 2 1 where the absolute coordinate of the center is XC1...

Страница 101: ...puted values are placed inside the circle with equation RL1 2 XL1 XC2 2 XD2 2 2 4 where the absolute coordinate of the center is XC2 and the diameter XD2 are adjustable After expiry of the associated...

Страница 102: ...1 ZL1 ZL1 Block1 Block1 Block3 Block1 Block3 BF Block1 BF Block1 Block1 Alpha40AL t40AL XC2 XD2 Element XC1 XD1 Element Alarm Element XC2 XD2 Start XC2 XD2 Start XC2 XD2 Trip XC1 XD1 Start XC1 XD1 Sta...

Страница 103: ...cy becomes lower than 20 Hz or higher than 70 Hz or all the phase voltages UL1 UL2 UL3 are lower than 1 En or all the phase currents IL1 IL2 IL3 are lower than 15 In Note 1 The common settings concern...

Страница 104: ...XD1 BF Enable ON Enable Block1 input ON Block Block1 Block1 0 without fault 0 if 20 f 70 Hz Block1 ON Inhibit AL40 inhibition 40ALdisbyXC1XD1 Start undervoltage Undervoltage enable ON Enable IL1L UL1...

Страница 105: ...f exceeding the adjustable threshold I2 Kheat is the machine thermal time constant at the inverse sequence current and IB is the base current When the inverse sequence current I2 drops below the thres...

Страница 106: ...failure BF The trip element can produce the Breaker Failure output if the I2 BF parameters are set to ON The parameters are available inside the Set Pro le A or B negative sequence overcurrent 46G I2...

Страница 107: ...graph inside CONTROL AND MONITOR ING section Fun F46G_AL ai I2 IAL RESET t2AL def 0 T TRIPPING M ATRIX LED REL AYS I2AL def t2AL def I2AL Start I2AL ST K I2AL TR K I2AL TR L I2AL ST L I2AL Start I2AL...

Страница 108: ...00 1000 10000 t s Kheat 0 1 s Kheat 0 5 s Kheat 1 0 s Kheat 5 0 s Kheat 10 0 s Kheat 40 0 s t2MAX 500 s I2 0 05 IB t2MIN 0 07 s Operating characteristic concerning the negative sequence element 46G wi...

Страница 109: ...0 100 1000 10000 t s Kheat 40 0 s Kheat 0 1 s Kheat 0 5 s Kheat 1 0 s Kheat 5 0 s Kheat 10 0 s Operating characteristic concerning the negative sequence element 46G with following settings Trip thresh...

Страница 110: ...nts above the associated pickup value are detected and a start is issued After expiry of the associated operate time t2 t2 a trip command is issued if instead the current drops below the threshold the...

Страница 111: ...if the I2 BF and or I2 BF parameters are set to ON The parameters are available inside the Set Pro le A or B negative sequence overcurrent 46 I2 Element I2 Element Setpoints menus 1 Note 1 The common...

Страница 112: ...One committed pilot wire input BLIN1 One or more binary inputs designed for input selective block One committed pilot wire output BLOUT1 One or more output relays designed for output selective block...

Страница 113: ...2 TR K I2 TR L I2 ST L I2 ST K I2 inv I2 I2 def I2 I2 inv I2 def T 0 t2CLP t2CLP Block1 Block2 A B C Starting control set A ON Change setting B OFF C ON Element blocking 1 1 A B C A ON Change setting...

Страница 114: ...nput I2 BLK2IN Block1 BLK2IN Iph Start I2 Trip I2 Iph Block2 IE Block2 BLK2IN IE tB timeout Block2 input tB K tB L Block1 FROM ANY PROTECTIONS FROM PHASE PROTECTIONS OFF ON IPh ON IPh IE ON IE BLIN1 B...

Страница 115: ...nt element 46 block diagram Output t2CLP I2 TR K I2 TR L I2 ST L I2 ST K I2 inv I2 I2 def I2 I2 inv I2 def T 0 t2CLP t2CLP Block1 Block2 A B C Starting control set A ON Change setting B OFF C ON Eleme...

Страница 116: ...input I2 BLK2IN Block1 BLK2IN Iph Start I2 Trip I2 Iph Block2 IE Block2 BLK2IN IE tB timeout Block2 input tB K tB L Block1 FROM ANY PROTECTIONS FROM PHASE PROTECTIONS OFF ON IPh ON IPh IE ON IE BLIN1...

Страница 117: ...ction check 47 47 Element Setpoints menu Logical block Block1 If the 47BLK1 enabling parameter is set to ON and a binary input is designed for logical block Block1 the element is blocked off whenever...

Страница 118: ...ovide an alarm signal to draw attention in the event of anoma lous heating without switching off the motor One of the above thresholds can be used to prevent motor starting when heating approaches the...

Страница 119: ...the DThCLP Mode parameter inside the Set Pro le A or B Thermal image 49MG Common con guration menu For both operating modes the DThCLP Activation time tDThCLP may be adjusted inside the Set Pro le A...

Страница 120: ...s designed for input selective block One committed pilot wire output BLOUT1 One or more output relays designed for output selective block Only when the committed pilot wire are used the continuity che...

Страница 121: ...ent blocking B or C DthAL1 L DthAL1 K 1 1 dD dt D T Ith IB 2 T dD dt D T 0 T T DThAL1 thermal image 49 block diagram A B C A ON Change setting A B C C ON Element blocking A B C B OFF Starting control...

Страница 122: ...K2IN Iph Iph Block2 IE Block2 BLK2IN IE tB timeout Block2 input tB K tB L Block1 FROM ANY PROTECTIONS FROM PHASE PROTECTIONS OFF ON IPh ON IPh IE ON IE BLIN1 Block1 T 0 tB IE Block2 IE 1 Block1 Block2...

Страница 123: ...INx tON INx tON INx tOFF 0 n o n c INx tOFF Motor restart Motor restart Motor restart LOW TH LOW TH Fun_49_AL2 ai D DthAL2 DthAL2 DthAL2 ON Enable element TRIPPING M ATRIX LED REL AYS DthAL2 Enable D...

Страница 124: ...K2IN Iph Iph Block2 IE Block2 BLK2IN IE tB timeout Block2 input tB K tB L Block1 FROM ANY PROTECTIONS FROM PHASE PROTECTIONS OFF ON IPh ON IPh IE ON IE BLIN1 Block1 T 0 tB IE Block2 IE 1 Block1 Block2...

Страница 125: ...FF 0 n o n c INx tOFF Motor restart Motor restart Motor restart LOW TH LOW TH Fun_49MG_Dth ai Dth D Dth Dth ON Enable element TRIPPING M ATRIX LED REL AYS Dth Enable Dth L Dth K BF Enable ON Enable Dt...

Страница 126: ...put Block1 BLK2IN Iph Iph Block2 IE Block2 BLK2IN IE tB timeout Block2 input tB K tB L Block1 FROM ANY PROTECTIONS FROM PHASE PROTECTIONS OFF ON IPh ON IPh IE ON IE BLIN1 Block1 T 0 tB IE Block2 IE 1...

Страница 127: ...ERISTICS 127 NVA100X D Manual 02 2016 F_49 1min Char ai Operating characteristic concerning the thermal image element 49MG T 1 min 1 1 1 2 3 4 5 6 7 8 9 10 20 Ith IB 0 01 0 1 1 10 100 1000 10000 1 0 p...

Страница 128: ...l 02 2016 FUNCTION CHARACTERISTICS F_49 200min Char ai Operating characteristic concerning the thermal image element 49MG T 200 min 1 1 1 2 3 4 5 6 7 8 9 10 20 Ith IB t s 0 1 1 10 100 1000 10000 10000...

Страница 129: ...nverse Time IEC 255 3 BS142 type C or EIT t 80 t H inv I I H inv 2 1 Moderately Inverse ANSI IEEE type MI t t H inv 0 01 I H inv 0 02 1 0 023 Very Inverse ANSI IEEE type VI t t H inv 3 922 I I H inv 2...

Страница 130: ...the CLP function Cold Load Pick up is enabled for element blocking the selected threshold may be blocked for an adjustable time interval starting from the circuit breaker closure This operating mode m...

Страница 131: ...tion Block1 BLK1I H CLPI H CLPI H Start I H Trip I H CLPI H I H Element BLK2OUT BLK4OUT BLK4OUT BLK2INI H BLK2INI H Start I H Trip I H I H BLK1 Block2 I H BLK2IN Start I2ndh I H 2ndh REST I H BLK2OUT...

Страница 132: ...e parameters are set to ON and a output relay is designed for selective block Block2 the protection issues a block output by phase elements BLK2OUT Iph or by any protection element BLK2OUT Iph IE when...

Страница 133: ...4 T 0 t H CLP 2nd harmonic restraint enable ON Enable I H 2ndh REST I H CLP Mode I H CLP def t H CLP I H CLP inv IL1H I H BF Enable ON Enable I H BF towards BF logic I H BF Trip I H TRIPPING M ATRIX L...

Страница 134: ...IPh Block2 IPh IE ModeBLIN1 T 0 tB Iph 50 51S1_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1I H BLK4IN I H BLK2IN I H Enable ON Enable I H BLK1 Block2 input enable ON Enable Pilot wire input I H BLK2IN Bloc...

Страница 135: ...e ON Enable I H 2ndh REST ICLP Mode t H CLP BF Enable ON Enable I H BF towards BF logic I H BF Trip I H TRIPPING M ATRIX LED REL AYS I H Curve 0 T A B C Output t H CLP I H Enable I H overcurrent eleme...

Страница 136: ...k2 IPh Block2 IPh IE ModeBLIN1 T 0 tB Iph 50 51S2_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1I H BLK4IN I H BLK2IN I H Enable ON Enable I H BLK1 Block2 input enable ON Enable Pilot wire input I BLK2IN Blo...

Страница 137: ...F logic I H BF Trip I H TRIPPING M ATRIX LED REL AYS A B C Output tCLP I H Enable I H overcurrent element 50 51 Block diagram tCLP Output tCLP CB State CB OPEN CB CLOSED CB OPEN t 0 1 s HIGH THRESHOLD...

Страница 138: ...INx tON INx tOFF T 0 n o n c INx tOFF Block2 IPh Block2 IPh IE ModeBLIN1 T 0 tB Iph 50 51S3_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1I H BLK4IN I H BLK2IN I H Enable ON Enable I H BLK1 Block2 input enab...

Страница 139: ...he motor nominal current but lower than the starting current at reduced voltage The minimum operate time is 0 1 s During starting the function is inhibited for an adjustable tLRCLP time slightly highe...

Страница 140: ...ents is lower than 0 1 IB the protection is blocked off If the CLP Source parameter is set to CB and the circuit breaker is open the protection is blocked off The CLP Source parameter common for pro l...

Страница 141: ...ST K tLR inv IL1L IL2L 1 1 ON Enable ILR element IL3L ILR Enable IL1L ILR inv ILR inv IL2L ILR inv ILR inv IL3L ILR inv ILR inv ILR overcurrent element 51LR block diagram Block1 Block2 STOP RUNNING Mo...

Страница 142: ...BLK2IN Iph Start ILR Trip ILR Iph Block2 IE Block2 BLK2IN IE tB timeout Block2 input tB K tB L Block1 FROM ANY PROTECTIONS FROM PHASE PROTECTIONS OFF ON IPh ON IPh IE ON IE BLIN1 Block1 T 0 tB IE Blo...

Страница 143: ...tON INx tON INx tOFF T 0 n o n c INx tOFF Speed control Speed control 0 0 Speed control 0 with speed control 1 without speed control 1 0 Mode51LR 0 0 without speed control with speed control Locked r...

Страница 144: ...ck1 BLK2IN Iph Start ILR Trip ILR Iph Block2 IE Block2 BLK2IN IE tB timeout Block2 input tB K tB L Block1 FROM ANY PROTECTIONS FROM PHASE PROTECTIONS OFF ON IPh ON IPh IE ON IE BLIN1 Block1 T 0 tB IE...

Страница 145: ...threshold with adjustable reduction factor K common to both thresholds when the voltage drops below an adjustable threshold U I U common to both thresh olds In addition the corresponding trip times m...

Страница 146: ...overcurrent element can produce the Breaker Failure output if the I I U BF and or I I U BF parameters are set to ON The parameters are available inside the Set Pro le A or B Voltage controlled restra...

Страница 147: ...ding the selectivity block criteria 2 The enable I I U BLK2IN and or I I U BLK2IN parameters are available inside the Set Pro le A or B Voltage controlled restraint overcurrent 51V I I U Element I I U...

Страница 148: ...I U def K KI I U I I U from I 51V element ON Inhibit I 51V inhibition t I U RES T 0 RESET t I U def 0 T I I U Start I I U Trip 74VT Block VT fault 74VT 0 without fault I I U Trip BF Enable ON Enable B...

Страница 149: ...T 0 n o n c INx tOFF Binary input INx T 0 Logic INx tON INx tON INx tOFF T 0 n o n c INx tOFF Binary input INx T 0 Logic INx tON INx tON INx tOFF T 0 n o n c INx tOFF Binary input INx T 0 Logic INx t...

Страница 150: ...K I I U TR K I I U TR L I I U ST L U12 U23 U I U U23 IL1L IL2L U31 IL1L threshold IL2L threshold U I U I I U def K KI I U I I U tI 51V RES T 0 RESET t I U def 0 T I I U Start I I U Trip 74VT Block VT...

Страница 151: ...F T 0 n o n c INx tOFF Binary input INx T 0 Logic INx tON INx tON INx tOFF T 0 n o n c INx tOFF Binary input INx T 0 Logic INx tON INx tON INx tOFF T 0 n o n c INx tOFF Binary input INx T 0 Logic INx...

Страница 152: ...faults The rst threshold trip may be inhibited by start of the second and or third threshold Similarly the second threshold trip may be inhibited by start of the third threshold Operation and setting...

Страница 153: ...he Set Pro le A or B Residual overcurrent 50N 1 51N 1 IE1 Element IE1 Element Setpoints menus Similarly the trip of the IE element may be inhibited by start of the third element IE by setting ONthe Di...

Страница 154: ...p IE1 Trip IE1 IE1 disbyIE IE1 BLK2IN IE disbyIE BLK1IE1 IE1 Element BLK2OUT Start IE1 Start IE1 Trip IE1 IE1 disbyIE IE BLK1 IE1 BLK2IN IE1 inhibition Block1 BLK1IE1 CLPIE1 CLPIE1 CLPIE1 IE1 Element...

Страница 155: ...T1 One or more output relays designed for output selective block Only when the committed pilot wire are used the continuity check of the pilot wire link is active Use of committed pilot wire input BLI...

Страница 156: ...all protective thresholds the following operating modes are available IN the element is enabled to receive the selective block from an internal input OUT the element is enabled to send the selective b...

Страница 157: ...enable ON Enable IE1 2ndh REST IE1CLP Mode tE1CLP BF Enable ON Enable IE1 BF towards BF logic IE1 BF Trip IE1 TRIPPING M ATRIX LED REL AYS IE1 Curve 0 T A B C A 1 A 0 or OFF Output tE1CLP IE1 Enable...

Страница 158: ...INx tOFF Binary input INx T 0 Logic INx tON INx tON INx tOFF T 0 n o n c INx tOFF Block2 IPh Block2 IPh IE ModeBLIN1 T 0 tB Iph 50N 51NS1_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1IE1 BLK4IN IE1 BLK2IN I...

Страница 159: ...Enable IE1 BF towards BF logic IE1 BF Trip IE1 TRIPPING M ATRIX LED REL AYS A B C Output tECLP IE1 Enable IE1 overcurrent element 50N 1 51N 1 Block diagram tE1CLP CB State CB OPEN CB CLOSED CB OPEN O...

Страница 160: ...OFF Binary input INx T 0 Logic INx tON INx tON INx tOFF T 0 n o n c INx tOFF Block2 IPh Block2 IPh IE ModeBLIN1 T 0 tB Iph 50N 51NS2_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1IE1 BLK4IN IE1 BLK2IN IE1 En...

Страница 161: ...T IE1CLP Mode tE1CLP BF Enable ON Enable IE1 BF towards BF logic IE1 BF Trip IE1 TRIPPING M ATRIX LED REL AYS A B C A ON Change setting B OFF C ON Element blocking Output tECLP IE1 Enable IE1 residual...

Страница 162: ...Binary input INx T 0 Logic INx tON INx tON INx tOFF T 0 n o n c INx tOFF Block2 IPh Block2 IPh IE ModeBLIN1 T 0 tB Iph 50N 51NS3_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1IE1 BLK4IN IE1 BLK2IN IE1 Enable...

Страница 163: ...inv 0 28 0236 IEC IEC inv 1 0 339 where t operate time IEC calculated residual current IECH for side H IECL for side L tEC inv pickup value tEC inv operate time setting For all inverse time characteri...

Страница 164: ...ged for an adjustable time interval starting from the circuit breaker closure The operating mode may be select by setting ON Element blocking or ON Change setting the IECCLP Mode IECCLP Mode IECCLP Mo...

Страница 165: ...ts BLK2OUT Iph or by any protection element BLK2OUT Iph IE whenever the given element Start IE Start IE and or Start IE becomes active The enable parameters ON or OFF are available inside the Set Pro...

Страница 166: ...Start IEC Trip IEC Start IEC Trip IEC CLPIE1 CLPIE1 IEC Element BLK2OUT BLK4OUT BLK4OUT BLK2INIEC BLK2INIEC IEC BLK1 Block2 IEC BLK2IN Start I2ndh IEC 2ndh REST IEC BLK2OUT Start I2ndh IEC 2ndh REST...

Страница 167: ...or OFF Output tECCLP IEC Enable IEC calculated residual overcurrent element Block diagram tECCLP CB State CB OPEN CB CLOSED CB OPEN Output tECCLP t 0 1 s HIGH THRESHOLD BLOCK LOW THRESHOLD UNBLOCK HIG...

Страница 168: ...N1 T 0 tB Iph 50N 51NS1_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1IEC BLK4IN IEC BLK2IN IEC Enable ON Enable Block2 input enable ON Enable Pilot wire input IEC BLK2IN Block1 BLK2IN Iph Iph Block2 IE Bloc...

Страница 169: ...B State CB OPEN CB CLOSED CB OPEN Output tECCLP t 0 1 s HIGH THRESHOLD BLOCK LOW THRESHOLD UNBLOCK HIGH THRESHOLD BLOCK A ON Change setting B OFF C ON Element blocking ON Inhibit Start IEC Start IEC I...

Страница 170: ...h IE ModeBLIN1 T 0 tB Iph 1 1 1 1 tB Iph tB IE BLK1IEC BLK4IN IEC BLK2IN IEC Enable ON Enable Block2 input enable ON Enable Pilot wire input IEC BLK2IN Block1 BLK2IN Iph Iph Block2 IE Block2 BLK2IN IE...

Страница 171: ...tECCLP IEC Enable IEC calculated residual overcurrent element Block diagram tECCLP CB State CB OPEN CB CLOSED CB OPEN Output tECCLP t 0 1 s HIGH THRESHOLD BLOCK LOW THRESHOLD UNBLOCK HIGH THRESHOLD BL...

Страница 172: ...IE ModeBLIN1 T 0 tB Iph 1 1 1 1 tB Iph tB IE BLK1IEC BLK4IN IEC BLK2IN IEC Enable ON Enable Block2 input enable ON Enable Pilot wire input IEC BLK2IN Block1 BLK2IN Iph Iph Block2 IE Block2 BLK2IN IE...

Страница 173: ...cos P S with Q 0 and the lead power factor are compared with the setting value cos lag cos lead Q Glag Q 2 Q Q 2 Q cosG Glead CPhi1 def CPhi1 def NO TRIP NO TRIP TRIP TRIP Q P P TRIP CPhi1 def CPhi1...

Страница 174: ...ing parameters are set to ON and a binary input is designed for logical block Block1 the concerning element is blocked off whenever the given input is active 2 The enabling parameter is available insi...

Страница 175: ...ion CB 55 tARM CPhi CB State CB 55 CB OPEN CB CLOSED Start enable CB OPEN Output tARM CPhi Output tARM CPhi t tARM CPhi G CPhi1 cosG CPhi1 0 G Q 0 Q 0 Q qualsiasi BF Enable ON Enable towards BF logic...

Страница 176: ...ion CB 55 tARM CPhi CB State CB 55 CB OPEN CB CLOSED Start enable CB OPEN Output tARM CPhi Output tARM CPhi t tARM CPhi G CPhi2 cosG CPhi2 0 G Q 0 Q 0 Q qualsiasi BF Enable ON Enable towards BF logic...

Страница 177: ...inverse time according the following characteristic curve t 0 5 tU inv U U inv 1 Where t operate time U inv threshold setting tU inv operate time setting For the inverse time characteristic following...

Страница 178: ...overvoltage elements 59 U U U Element U Element Start U Start U Start U Trip U Trip U U disbyU U inhibition tU def tU inv U def tU def U def U inv U Curve U Enable State Block1 BLK1U U BLK1 Start U B...

Страница 179: ...e the Set Board1 2 inputs Binary input IN1 1 INx x menus All the parameters can be set separately for Pro le A and Pro le B Note 1 The exhaustive treatment of the logical block Block 1 function may be...

Страница 180: ...v t U inv 100 s t U inv 10 s t U inv 1 s t U inv 0 1 s 1 5 0 01 0 1 1 10 100 1000 10000 t s t tU inv U U inv 1 0 5 Inverse time operating characteristic concerning the rst threshold U of the overvolta...

Страница 181: ...asure of UEC for VTs input versions or ThySensor where UE measured residual voltage UEC calculated residual voltage t operate time UE inv threshold setting tUE inv operate time setting For the inverse...

Страница 182: ...counting starts when the input block goes down 3 The enabling parameters are available inside the Set Pro le A or B Residual overvoltage 59N UE Element UE Element Setpoints menus while the Block1 func...

Страница 183: ...l overvoltage element UE Enable UE UE def UE inv 1 State UE UE def UE UE inv State Logic diagram concerning the rst threshold UE of the residual overvoltage element 59N Fun F59N_S2 ai 1 Block 74VT ON...

Страница 184: ...1 s 1 5 0 01 0 1 1 10 100 1000 10000 t s t tUE inv UE UE inv 1 0 5 t tUE inv UEC UE inv 1 0 5 UE UE inv UEC UE inv Inverse time operating characteristic concerning the rst threshold UE of the residual...

Страница 185: ...ement Setpoints menu 1 Logical block Block1 If the U2 BLK1 enabling parameter is set to ON and a binary input is designed for logical block Block1 the protection is blocked off whenever the given inpu...

Страница 186: ...art U2 U2 TR K U2 ST L U2 TR L Trip U2 Trip U2 Trip U2 BF Enable ON Enable U1 BF towards BF logic BLK1U2 U2 BF Enable ON Enable Block1 input ON Block U1 BLK1 Block1 Block1 U2 Binary input INx T 0 Logi...

Страница 187: ...orresponding setting is C7 C8 POL NORMAL pE1 1 otherwise is INVERSE pE1 1 The C7 C8 POL parameter is available inside the Set Polarity menu ME is an amplitude compensating factor of residual current c...

Страница 188: ...xternal earth fault If any CT is saturated a displacement angle 180 is introduced so the stabilization current is decreased In particular the maximum stability on external fault is obtained with 100 C...

Страница 189: ...never the given element Start 64REF becomes active The enable 64REF BLK2OUT parameter ONor OFF is available inside the Set Pro le A or B Low impedance restricted ground fault 64REF while the BLK2OUT I...

Страница 190: ...ocked rotor threshold overcome inside an adjust able time control window may be programmed by setting the Type66 parameter NTS TST and available inside the Set Pro le A or B Maximum number of starts 6...

Страница 191: ...1 IL3 Starting detection Type66 NST Max number of starts Any change of Type66 setting Type66 TST Cumulative time of starts Type66 NST Maximum number of starts Type66 TST Max starting span t Max IL1 IL...

Страница 192: ...Moderately Inverse ANSI IEEE type MI t tED inv 0 01 IED IED inv 0 02 1 0 023 Very Inverse ANSI IEEE type VI t tED inv 3 922 IED IED inv 2 1 0 098 Extremely Inverse ANSI IEEE type EI t tED inv 5 64 IE...

Страница 193: ...isplacement of the characteristic axis standing for the trip bisector of the tripping zone For isolated neutral systems with a 90 characteristic angle setting faults towards the LINE are detected whil...

Страница 194: ...4VText function must be assigned to the selected binary inputs inside the Set Board 1 2 inputs Binary input IN1 1 IN1 x menus For all the four thresholds common for all thresholds an insensibility zon...

Страница 195: ...the characteristic axis IE2 cos E E 0 AND The residual current projection on the characteristic axis IE2 cos E E overcomes the threshold IED IED IED IED AND The residual voltage UE or UEC fundamental...

Страница 196: ...setting ON the Disable IED by start IED start IED IED disbyIED IED disbyIED parameter available inside the Set Pro le A or B Directional earth fault overcurrent 67N IED Element IED Element Setpoints...

Страница 197: ...rogramming the ModeBLOUT1 parameter OFF ON IPh ON IPh IE ON IE inside Set Pro le A or B Selective block BLOCK2 Selective block OUT menus Use of output relay If the IED BLK2OUT IED BLK2OUT IED BLK2OUT...

Страница 198: ...ition IED inhibition Block1 BLK1IED IED BLK1 Start IED IED BLK2IN BLK2INIED Block2 Start IED BLK2INIED Block2 IED BLK2IN Start IED BLK1IED IED BLK1 Block1 Start IED IE2 tED def IEDCLP def IED def IEDC...

Страница 199: ...CLP A OFF A ON Change setting within CLP A ON CLP A OFF 1 State UED inv UED def UED inv UED def State IE2 1 IEDCLP def IEDCLP inv IEDCLP State IED inv IED def IED inv IED def State 1 State UED inv M U...

Страница 200: ...tting within CLP A ON A OFF 1 State UED inv UED def UED inv UED def State 3Vo IE2 IE2 cos 0 1 State UED inv M UED def M UED inv UED def State 1 State UED inv UED def UED inv UED def State 3Vo IE2 TRIP...

Страница 201: ...setting within CLP B OFF CLP disabled C ON Element blocking within CLP 1 CLP IED IE2 IEDCLP def IEDCLP def State IED def IED def Block by 74VT ON Block Internal or external OFF 74VT 74VTint ext67N tE...

Страница 202: ...Block2 IPh IE ModeBLIN1 T 0 tB Iph 67NS1_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1IED BLK4IN IED BLK2IN IED Enable ON Enable IED BLK1 Block2 input enable ON Enable Pilot wire input IED BLK2IN Block1 BL...

Страница 203: ...inside trip sector 1 A ON Change setting within CLP A ON CLP A OFF A ON Change setting within CLP A ON CLP A OFF A ON Change setting within CLP A ON CLP A OFF 1 State UED inv UED def UED inv UED def S...

Страница 204: ...State IE2 cos M IED def OFF ON Insens Zone E inside trip sector IE2 E inside trip sector 1 A ON Change setting within CLP A ON A OFF 1 State UED inv UED def UED inv UED def State 3Vo IE2 IE cos 0 1 St...

Страница 205: ...setting within CLP B OFF CLP disabled C ON Element blocking within CLP 1 CLP IED IE2 IEDCLP def IEDCLP def State IED def IED def Block by 74VT ON Block Internal or external OFF 74VT 74VTint ext67N tED...

Страница 206: ...Ph Block2 IPh IE ModeBLIN1 T 0 tB Iph 67NS2_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1IED BLK4IN IED BLK2IN IED Enable ON Enable IED BLK1 Block2 input enable ON Enable Pilot wire input IED BLK2IN Block1...

Страница 207: ...ctor 1 A ON Change setting within CLP A ON CLP A OFF A ON Change setting within CLP A ON CLP A OFF A ON Change setting within CLP A ON CLP A OFF 3Vo State UED def UED def 3Vo State UED def M UED def 3...

Страница 208: ...3Vo IE2 IE cos 0 3Vo IE2 TRIP 3Vo IE2 TRIP A ON Change setting within CLP A ON CLP A OFF IE2 Common con gurations Insens Zone OFF ON UE UEC 3Votype67N 3Vo I I cos Mode67N M threshold M Insens Zone OFF...

Страница 209: ...4 A ON Change setting within CLP B OFF CLP disabled C ON Element blocking within CLP 1 CLP IED IE2 IEDCLP def IEDCLP def State IED def IED def Block by 74VT ON Block Internal or external OFF 74VT 74VT...

Страница 210: ...h Block2 IPh IE ModeBLIN1 T 0 tB Iph 67NS3_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1IED BLK4IN IED BLK2IN IED Enable ON Enable IED BLK1 Block2 input enable ON Enable Pilot wire input IED BLK2IN Block1 B...

Страница 211: ...ector 1 A ON Change setting within CLP A ON CLP A OFF A ON Change setting within CLP A ON CLP A OFF A ON Change setting within CLP A ON CLP A OFF 3Vo State UED def UED def 3Vo State UED def M UED def...

Страница 212: ...A ON A OFF 3Vo IE2 IE2 cos 0 3Vo IE2 TRIP 3Vo IE2 TRIP A ON Change setting within CLP A ON CLP A OFF IE2 Common con gurations Insens Zone OFF ON UE UEC 3Votype67N 3Vo I I cos Mode67N M threshold M Ins...

Страница 213: ...A ON Change setting within CLP B OFF CLP disabled C ON Element blocking within CLP 1 CLP IED IE2 IEDCLP def IEDCLP def State IED def IED def Block by 74VT ON Block Internal or external OFF 74VT 74VTi...

Страница 214: ...Ph Block2 IPh IE ModeBLIN1 T 0 tB Iph 67NS4_BL diagram ai 1 1 1 1 tB Iph tB IE BLK1IED BLK4IN IED BLK2IN IED Enable ON Enable IED BLK1 Block2 input enable ON Enable Pilot wire input IED BLK2IN Block1...

Страница 215: ...Inverse Time IEC 255 3 BS142 type B or VIT t 13 5 tEDC inv IEDC IECD inv 1 Extremely Inverse Time IEC 255 3 BS142 type C or EIT t 80 tEDC inv IEDC IEDC inv 2 1 Moderately Inverse ANSI IEEE type MI t t...

Страница 216: ...sures Calculated residual current on side H the calculated IECH current is employed where the funda mental component and phase are derived from the instantaneous values of the three input phase curren...

Страница 217: ...74VT Block all the four thresholds are blocked when the 74VT external signal is active Not directional all the four thresholds are switched from directional to not directional criteria when the 74VT...

Страница 218: ...uration menu The settable operating mode is I module or I cos projection Projection If the projection principle and he operation mode is not switched to not directional by the 74VT function the start...

Страница 219: ...IEDC Element IEDC Element IEDC Element Setpoints menus Similarly the trip of the IEDC elementmaybeinhibitedbystartofthethirdand orfourthelement IEDC and orIEDC by setting ON the Disable IEDC by start...

Страница 220: ...mation about phase or phase earth block may be select programming the ModeBLIN1 parameter inside the Set Pro le A or B Selective block BLOCK2 Selective block IN menus Use of binary inputs If the IEDC...

Страница 221: ...the element is disabled to send receive the internal selective block Transmission and reception for the same element is not allowed so any stall situation due to wrong setting is avoided The internal...

Страница 222: ...C Enable IEDC inhibition IEDC inhibition IEDC inhibition Block1 BLK1IEDC IEDC BLK1 Start IEDC IEDC BLK2IN BLK2INIEDC Block2 Start IEDC BLK2INIED Block2 IEDC BLK2IN Start IEDC BLK1IEDC IEDC BLK1 Block1...

Страница 223: ...ED inv UED def UED inv UED def State IEC 1 IEDCCLP def IEDCCLP inv IEDCCLP State IEDC inv IEDC def IEDC inv IEDCD def State 1 State UED inv M UED def M UED inv UED def State IE 1 IEDCCLP def IEDCCLP i...

Страница 224: ...os M IEDC def OFF ON Insens Zone E inside trip sector IEC E inside trip sector 1 A ON Change setting within CLP A ON A OFF 1 State UED inv UED def UED inv UED def State 3Vo IEC IE cos 0 1 State UED in...

Страница 225: ...abled C ON Element blocking within CLP 1 CLP IEDC IEC IEDCCLP def IEDCCLP def State IEDC def IEDC def Block by 74VT ON Block Internal or external OFF 74VT 74VTint ext67NC tED RES T 0 RESET tEDC def in...

Страница 226: ...e IEDC BLK1 Block2 input enable ON Enable Pilot wire input IEDC BLK2IN Block1 BLK2IN Iph Start IEDC Trip IEDC Iph Block2 IE Block2 BLK2IN IE tB timeout Block2 input tB K tB L Block1 FROM EARTH FAULT P...

Страница 227: ...or a tfEN adjustable time Setting of the tfEN value is available inside the Set Base menu with level 1 session The rst threshold trip f may be inhibited by start of the second threshold f by setting O...

Страница 228: ...nside CONTROL AND MONITOR ING section Fun F81O_S1 ai f inhibition ON Inhibit RESET tf def 0 T TRIPPING M ATRIX LED REL AYS tf def f Start f Start f Trip f Trip f Trip BF Enable ON Enable f BF towards...

Страница 229: ...by setting ON the Disable f by start f Disable f by start f Disable f by start f f disbyf f disbyf f disbyf parameters available inside the Set Pro le A or B Underfrequency 81U f Element f Element f E...

Страница 230: ...ING section Fun F81U_S1 ai RESET tf def 0 T TRIPPING M ATRIX LED REL AYS f Start f Start f Trip f Trip f Trip BF Enable ON Enable towards BF logic Block1 f BF Enable ON Enable Block1 input ON Block f...

Страница 231: ...K f TR L f BLK1 UL1 UL2 UL3 Max UL1 UL2 UL3 20 Un Logic diagram concerning the third threshold f of the underfrequency element 81U RESET tf def 0 T TRIPPING M ATRIX LED REL AYS tf def f Start f Start...

Страница 232: ...se current on side L iL2C L instantaneous value of L2 compensated phase current on side L iL3C L instantaneous value of L3 compensated phase current on side L With compact notation the previous vector...

Страница 233: ...e reference chosen by the relay is the one with the lowest mismatching coef cient If the two sides have an equal value of the mismatching coef cient the reference is chosen as the side with the index...

Страница 234: ...ce choice for the current phase compensation programming parameters from Conn H and Conn L parameters inside the Set Transformer menu the delta winding D or d programming or zig zag Z or z programming...

Страница 235: ...ary delta closed short circuit transformation ratio of 1 3 that removes the component from the zero sequence compensated current for the side w The connection of the secondary phase of the CT adapters...

Страница 236: ...transformation ratio of 1 3 that removes the component from the zero sequence compensated current for the side w The connection of the secondary phase of the CT adapters to the relay inputs is L3 L1...

Страница 237: ...rms value of fundamental component of the instantaneous val ues x using DFT Discrete Fourier Transform It is noted that the effective values of the fundamental component of the stabilization currents...

Страница 238: ...de nite time Similarly the start of the rst threshold of the differential protection on L2 ST Id L2 or L3 ST Id L3 phase occurs when all the following conditions are met 87 Enable ON IdL2 Id IdL2 K1 1...

Страница 239: ...ive block Block2 With single enable ag for rst or second threshold of differential protection the element can pro duce the output block committed pilot wire or output relay programmed for logic select...

Страница 240: ...straint setting 2nd REST the start of the second harmonic restraint in the corresponding phase goes ON ST 2nd REST L1 or ST 2nd REST L2 or ST 2nd REST L3 If at least one ratio Id5L1 IdL1 Id5L2 IdL2 Id...

Страница 241: ...the zero crossing of the instantaneous values of stabiliza tion current in a phase the level of instantaneous values of the differential current at that phase is controlled by the relay In the case o...

Страница 242: ...iL1c L iL1 L iL2 L iL3 L M H P H C H SIDE L MatchType Inct L PhSeq pL1 L pL2 L pL3 L ProtObj NumSides Sn L Vn L Gnd L Conn L VectGroup L iLxc L iLxc H iLx H SIDE H iLx L SIDE L Magnitude polarity pha...

Страница 243: ...ST L2 Id2L2 Id1L2 0 T ST 2nd REST L3 Id2L3 Id1L3 Id5L1 Id5L2 Id5L3 Id2L1 DFT2 Id2L2 DFT2 Id2L3 5th REST CROSS H REST 2nd REST tHREST RES 1 1 1 1 1 ST H REST L2 1 idL1 L3 IdL1 L3 A ON A OFF to biased d...

Страница 244: ...L2 ST Id L2 Id1L2 K1 100 ISL2 Id1L2 Id Id Id1L2 Id K2 Q Id1L2 K2 100 ISL2 Q IdL2 ISL2 Id K1 ST Id L3 ST Id L3 Id1L3 K1 100 ISL3 Id1L3 Id Id Id1L3 Id K2 Q Id1L3 K2 100 ISL3 Q IdL3 ISL3 from saturation...

Страница 245: ...output ON Enable 87TBLK2OUT Block4 in out diagram Logic diagram of the logic blocking signals Block4 tFI Iph ST IE BLK4 ST Iph BLK4 1 1 tFI IE Block4 OUT 1 T 0 tFI Iph T 0 tFI IE xx Block4 OUT Block4...

Страница 246: ...their starts are required start reset is faster than trip reset The element may be enabled or disabled by setting ON the BF Enable parameter available inside the Set Pro le A or B Breaker failure BF...

Страница 247: ...ock1 52a IBF Max IL1L IL3L IBF IL1L IL2L IL3L IEBF IE IEBF IE1 1 RESET tBF 0 T tBF 1 Binary input INx T 0 Logic INx tON INx tON INx tOFF T 0 n o n c INx tOFF Binary input INx T 0 Logic INx tON INx tON...

Страница 248: ...ical block it is not liable for any inhibition time out so the protective element is disabled for the whole time when the input is ON 2 Note 1 In the following treatment the logical block is de ned as...

Страница 249: ...51 element side L I L BLK1 50 51 element side L IE1 BLK1 50N 1 51N 1 element IE1 BLK1 50N 1 51N 1 element IE1 BLK1 50N 1 51N 1 element IEC BLK1 50N Comp element IEC BLK1 50N Comp element IE1 BLK1 50N...

Страница 250: ...f binary inputs If the xxBLK2IN parameters enable are set to ON and a binary input is designed for selective block Block2 the protection is blocked off by phase elements Block2 Iph by earth elements B...

Страница 251: ...rt circuit of the pilot wires concerning the same line Note 1 In the absence of suitable provisions a short circuit on a pilot wire causes the block of the receiving relay so a possible fault contempo...

Страница 252: ...ter inside the Set Pro le A or B Selective block BLOCK2 Selective block OUT menu The parameters can be set separately for A and B pro les Operation The selective block outputs go ON at the same time o...

Страница 253: ...disabled 2 If no pulses are received inside an adjustable time window at the selective block input circuit a break pilot wire alarm is issued the information is available for reading Breaked BLIN1data...

Страница 254: ...blocked by start of B and or C protection Settings I def 4 5 In t def 0 100 s PulseBLOUT1 OFF PulseBLIN1 1 s I BLK2IN ON I BLK2OUT OFF tB IPh 0 30 s B Protection I element with de nite time set to 4 0...

Страница 255: ...input and output the element is always OFF no trip If the xxx threshold start stay ON within the operating time and the internal input is OFF when the timer expires the trip goes ON If the xxx thresho...

Страница 256: ...ans of internal selective block Block4 With the following setting for P1 and P2 protection relay I BLK4IN IN I Internal selective block input IPD BLK4IN OUT IPD Internal selective block output IE BLK4...

Страница 257: ...IPD internal block output of P2 relay BLK4OUT IPD internal block output of P1 relay BLK4IN I I internal block input of P2 relay BLK4IN I I internal block input of P1 relay tPD tFI Iph t Trip I P1 rela...

Страница 258: ...g g g Phase overcurrent 50 51 I H side H Element g g g g Phase overcurrent 50 51 I H side H Element g g g g Phase overcurrent 50 51 side L I L Element g g g g Phase overcurrent 50 51 side L I L Eleme...

Страница 259: ...ectional earth fault overcurrent calculated residual current 67N IEDC Element g g g g Directional earth fault overcurrent calculated residual current 67N IEDC Element g g g g Directional earth fault o...

Страница 260: ...ero the Logic parameters ON OFF must be pro grammed in the same way of the related circuit connected with it The RemTrip K matching must be assigned to the selected output relays inside the Set Remote...

Страница 261: ...ent is performed on the current signals IL1L IL2L IL3L If the larger phase input current is lower than 25 In and the larger phase input voltage is lower than 1 5 En the sampling frequency is xed to fn...

Страница 262: ...gs Each second harmonic component of phase currents IL1 2nd IL2 2nd IL3 2nd is compared with the I2ndh adjustable threshold When one or more currents overcome the setting threshold a start is issued T...

Страница 263: ...on would occur on imbalance transient secondary current due to asymmetric line CTs saturation Depending upon the magnitude and duration of the starting current it may be necessary to block operation o...

Страница 264: ...rder to avoid unwanted tripping due to unblocked threshold or threshold with his original value for cases where a delay of the circuit breaker closing happen i e where the three poles of the CB do not...

Страница 265: ...B OFF C ON Element blocking 1 1 A B C A ON Change setting A B C C ON Element blocking A B C B OFF Starting control CLP source MR Enable CB State IRUN 0 1IB Max IL1 IL3 IRUN IL1 IL3 Output tCLP tCLP M...

Страница 266: ...I L Element g g Phase overcurrent side L 50 51 I H Element g g Residual overcurrent 50N 1 51N 1 IE1 Element g g Residual overcurrent 50N 1 51N 1 IE1 Element g g Residual overcurrent 50N 1 51N 1 IE1 E...

Страница 267: ...inside the Set CT supervision 74CT side H and Set CT supervision 74CT side L submenu the same for ad dressing the LED indicators S H TR L and S L TR L Logical block Block1 If the S BLK1parameter is s...

Страница 268: ...han an adjustable threshold IVT the latter must be adjusted to a value higher than the current at energisation and lower than the short circuit current When any of the previous condition is detected t...

Страница 269: ...its Activates 74VT if all phase voltages are lost with loaded generator Activates 74VT if all phase voltages are lost during commissioning of the line voltage TV not connected checking that no of the...

Страница 270: ...he trip timer is held in reset condition so the operate time counting starts when the input block goes down The 74TCS BLK1 parameter is available inside the Set Pro le A B Trip circuit supervision 74T...

Страница 271: ...r a 40 s delay in order to allow the fault clearing and the consequent reset of the TRIP protection Outputs are reset to zero after 6 s from the TRIP contact open 1 Note 1 The trip contact TRIP of the...

Страница 272: ...chosen between the Rmin and Rmax values typically the normalized value nearest the arithmetic mean R Rmin Rmax 2 The power dissipated by the R resistor is PR R I 2 R UAUX R RTC 2 Example UAUX 110 Vcc...

Страница 273: ...n K and CBclose K function must be set inside the Set Circuit breaker supervision LEDs relays allocation menu the CB position can be visualized by means two LEDs CBopen L and CBclosed L parameters All...

Страница 274: ...k L TRIPPING M ATRIX LED REL AYS TRIPPING M ATRIX LED REL AYS TRIPPING M ATRIX LED REL AYS State N Open tbreak State SumI Opening transition N Open Mode N Open From CB position Opening transition Mode...

Страница 275: ...this allows to reduce the clearing time that in time logic systems require trip time signi cantly long in correspondence of the power source Circuit breaker commands Selection of setting pro les Remot...

Страница 276: ...energy measures g g g 74VT ext 74VT from external relays g g g I L Bk Block1 threshold I side L g g g I L Bk Block1 threshold I side L g g g I L Bk Block1 threshold I side L g g g I H Bk Block1 thres...

Страница 277: ...ST g g I L ST g g I H ST g g I H ST g g I H ST g g Id ST g g Id ST g g IE1 ST g g IE1 ST g g IE1 ST g g IE2 ST g g IE2 ST g g IE2 ST g g IEC ST g g IEC ST g g IEC ST g g IED ST g g IED ST g g IED ST g...

Страница 278: ...Trip B Input Mask1 Input Mask2 Start A Start B Trip A Trip B Input Mask1 Input Mask2 74TCS TR g g BF TR g g TEST_TRIP g g IN1 g g IN2 g g IN3 g g IN4 g g IN5 g g IN6 g g IN7 g g IN8 g g IN9 g g IN10...

Страница 279: ...ters available inside the Set Oscillography Trigger Setup menu are user pro grammable Pre trigger time and Post trigger time Element pickup trigger the information recording starts when a state transi...

Страница 280: ...se to phase voltages U12 U23 U31 Calculated residual voltage UEC Calculated residual current side H and side L IECH IECL Maximum current between IL1L IL2L IL3L ILmaxL Minimum current between IL1L IL2L...

Страница 281: ...onic phase currents IL1L 4th IL2L 4th IL3L 4th Fifth harmonic phase currents IL1L 5th IL2L 5th IL3L 5th Motor starts Starts number NStart Total start time TStart Demand phase Phase xed currents demand...

Страница 282: ...OFF Block I L Logic block side L active with virtual I O BlockI L ON OFF Block I L Logic block side L active with virtual I O BlockI L ON OFF Block I H Logic block side H active with virtual I O Bloc...

Страница 283: ...nters CB Counters 74VT Counters 74CT side H Counters 74CT side L Counters BF Counters Partial counters xx Start partial counter xx I I 0 9999 xx Trip partial counter xx I I 0 9999 xx Block1 partial co...

Страница 284: ...ated to an output relay for this purpose the Self test relay pa rameter can be set inside the Set Self test Relay submenu Pilot wire diagnostic Detailed diagnostic information about the pilot wire are...

Страница 285: ...ord Event counter 2 Date and time Event cause binary input element trip setting change Oscillography DFR Upon programmable trigger the fault records are recorded in COMTRADE format the sampled mea sur...

Страница 286: ...3H Side L RMS value of fundamental of phase currents IL1L IL2L IL3L RMS value of fundamental of phase voltages UL1 UL2 UL3 Side 1 RMS value of fundamental of residual current IE1 Side 2 RMS value of f...

Страница 287: ...f frequency Example 1 With the following setting Pre trigger 0 25 s Post trigger 0 25 s Sampled measures iL1H iL2H iL3H iL1L iL2L iL3L idL1 idL2 idL3 iE1 iE2 Analog measures IL1H IL2H IL3H IL1L IL2L I...

Страница 288: ...ts is mounted on the front of electric control board previously drilled as indicated in the drawing In case of side by side mounting of several relays the minimum drilling distance is determined by th...

Страница 289: ...00X D Manual 02 2016 Remove the two vertical frames for access the holes for the xing screws the frames are snapped Insert the device into the slot Fit the device to the panel with four screws Replace...

Страница 290: ...ounting For mounting inside a standardized 19 inch system EIA 310 D IEC 60297 and DIN 41494 SC48D the MAR adapter is required available on request Rack mounting Rack mount ai 177 4U 101 6 482 6 465 Ra...

Страница 291: ...e relay or checks on the amperometric circuits is essential to provide appropriate support to achieve the secondary circuit shorting For security reasons it is advisable to operate in the absence of l...

Страница 292: ...S cross sectional area of the current conductors expressed in mm2 It is recommended that cabling of a suitable thickness be used in order to limit wear of the CT sec ondary circuits Earth connection...

Страница 293: ...he transformer so that the magnetic effect of the three cables is perfectly compensated in the absence of residual current Fig 2a Hence the assembly indicated in the drawing of g 2b in which phase L3...

Страница 294: ...at the relay side Binary inputs UAUX UAUX A B IN1C IN2D 11 12 13 14 15 16 17 18 19 20 BINARY INPUTS 1 IN1 1 IN1 2 IN1 3 IN1 4 IN1 5 IN1 6 IN1 7 IN1 8 IN1 9 IN1 10 IN1 11 IN1 12 IN1 13 IN1 14 IN1 15 IN...

Страница 295: ...ion methods are available SNTP protocol Simple Network Time Protocol over Ethernet network IRIG B Inter Range Instrumentation Group Time Code Format B Local port A cross cable must be employed When us...

Страница 296: ...onegotiation parameter of device Autonegotiation parameter inside Com munication Ethernet submenu Note 1 The TX RJ45 and FX bra ottica Ethernet port are multiplexed single IP address Under normal cond...

Страница 297: ...provided resistor termination can be made by means a jumper between the F2 F3 terminals Termination resistors allow adjusting the impedance of the line reducing the in uence of the induc tive componen...

Страница 298: ...the committed pilot wire circuits Logic selectivity with BFO Block sch ai BLIN1 BLIN1 BLIN1 Block2 IPh BLOUT1 BLOUT1 TRIP I TRIP I TRIP I TRIP I Any device Logic selectivity with BFO Block sch ai BLI...

Страница 299: ...p information of any protective functions LED 1 13 red are freely assignable from the user to any protective and or control functions 6 6 FINAL OPERATIONS Before energizing the electric board it is ad...

Страница 300: ...t site Products Software 1 ThySetter use Please refer to ThySetter user manual for detailed instructions The document is available on www thytronic it Product Software ThySetter Download area Note 1 S...

Страница 301: ...points out the auxiliary power supply voltage permanent and possible diagnostic faults blink The display backlight is automatically activated when any key switch is set By means of the Up or Down but...

Страница 302: ...to the NA80 relay As example to set the operating mode of the K1 output relay as ENERGIZED LATCHED the following procedure must be issued By means Down button select the Set menu SET Press the Right...

Страница 303: ...buttons it is possible to browse the main menu till the RS485 Protocol or Ethernet parameters message to enter you must press the Right button As example to select the address 12 for the ModBus protoc...

Страница 304: ...he menu command Communication Open Verify that inside the modality box Serial and Automatic are selected Thysetter will search automatically the relay from the template regardless of what is selected...

Страница 305: ...r about 3 minutes elapsed without pressing any button If you do not want to wait three minutes of waiting it must go back to the password menu and come out without input any data and until the the mes...

Страница 306: ...H 0 000 InH IESH 0 000 IE1n DTheta 0 DThetaB ILmaxL 0 000 InL ILminL 0 000 InL ILL 0 000 InL ILmaxH 0 000 InH ILminH 0 000 InH ILH 0 000 InH ILmaxL rms0 000 InL ILminL rms0 000 InL ILL rms 0 000 InL U...

Страница 307: ...P IEC OFF BLK1 IEC OFF BLK2IN IEC OFF BLK4IN IEC OFF Start IEC OFF Trip IEC OFF CLP IEC OFF BLK1 IEC OFF BLK2IN IEC OFF BLK4IN IEC OFF 50N C 51N C 32P Start P1 OFF Trip P1 OFF BLK1 P1 OFF Start P2 OFF...

Страница 308: ...C OFF BLK4INIEDC OFF 67N C Start Id L1 OFF Trip Id L1 OFF Start Id L2 OFF Trip Id L2 OFF Start Id L3 OFF Trip Id L3 OFF Start Id OFF Trip Id OFF BLK1 Id OFF Start Id L1 OFF Trip Id L1 OFF Start Id L2...

Страница 309: ...Lr 0 000 InL IE2r 0 000 IEn2 IECHr 0 000 InH IESHr 0 000 IEn1 UEr 0 000 UEn UECr 0 000 UECn PhiL1r 0 deg PhiL2r 0 deg PhiL3r 0 deg PhiEr 0 deg PhiECr 0 deg PhiE IECr 0 deg PhiEC IECr 0 deg DTheta r 0...

Страница 310: ...2IED cnt 0 ParStIED cnt 0 ParTrIED cnt 0 ParBk1IED cnt 0 ParBk2IED cnt 0 74CT side H Counters ParBk1 74CTHcnt 0 ParTr74CTHcnt 0 74CT Counters ParBk1 74CTLcnt 0 ParTr74CTLcnt 0 BF Counters ParStBFcnt 0...

Страница 311: ...t 0 TotTrIED cnt 0 TotBk1IED cnt 0 TotBk2IED cnt 0 TotStIED cnt 0 TotTrIED cnt 0 TotBk1IED cnt 0 TotBk2IED cnt 0 74CT side H Counters TotBk1 74CTHcnt 0 TotTr74CTHcnt 0 74CT Counters TotBk1 74CTLcnt 0...

Страница 312: ...ints Binary input IN1 x Setpoints IB IB 1 00 In U Enable OFF Type Characteristic U Curve DEFINITE U def OFF 0 5 Un tU def 1 s U inv OFF 0 5 Un tU inv 10 s U BF OFF Relays U U ST K U TR K LEDs U U ST L...

Страница 313: ...nt XC1XD1 Element XC2XD2 Element 46M I2 Element Q2 Element I2 Enable OFF I2CLP Mode OFF t2CLP 0 10 s t2 RES 0 00 s I2 def OFF 1 00 IB I2CLP def 2 00 IB t2 def 1 00 s I2 BLK1 OFF I2 BLK2IN OFF I2 BLK2O...

Страница 314: ...I inv OFF 1 00 In ICLP inv 2 00 In t inv 10 0 s I BLK1 OFF I BLK2IN OFF I BLK2OUT OFF I BLK4 OFF I 2ndh REST OFF I BF OFF Relays I I ST K I TR K LEDs I I ST L I TR L I Enable OFF ST I ST U OFF ICLP M...

Страница 315: ...E2 RES 0 00 s IE2 def OFF 1 00 IEn1 IE2CLP def 2 00IEn2 tE2 def 1 00 s Relays IE2 IE2 ST K IE2 TR K LEDs IE2 IE2 ST L IE2 TR L IE2 Enable OFF Type Characteristic IE2 Curve DEFINITE IE2CLP Mode OFF tE2...

Страница 316: ...64REF BF OFF Relays 64REF 64REF ST K 64REF TR K LEDs 64REF 64REF ST L 64REF TR L 66 66 Enable OFF Type66 NST tC 1 min NST 10 TST 30 s TIN 0 min 66BLK1 OFF Relays 66 66 TR K LEDs 66 66 TR L 59N Common...

Страница 317: ...ED def 1 00 s IED inv OFF 1 00 IEn UED inv 0 100 UEn ThetaE inv 60 gr BetaE inv 45 gr IEDCLP inv1 5 IEn2 tED inv 10 0 s IED BLK1 OFF IED BLK2IN OFF IED BLK2OUT OFF IED BLK4 OFF IED BF OFF IED disbyIED...

Страница 318: ...BetaEC def45 gr IEDCCLP def1 5 In tEDC def 1 00 s IEDC BLK1 OFF IEDC BLK2IN OFF IEDC BLK2OUTOFF IEDC BLK4 OFF IEDC BF OFF IEDC disIEDC OFF IEDC disIEDC OFF IEDC disIEDC OFF Relays IEDC IEDC ST K IEDC...

Страница 319: ...BLOUT1 OFF tF IPh 1 00 s tF IE 1 00 s tF IPh IE 1 00 s Relays BLOCK2OUT BLOCK2OUT IPh K BLOCK2OUT IE K BLOCK2OUT IPh IE K LEDs BLOCK2OUT BLOCK2OUT IPh L BLOCK2OUT IE L BLOCK2OUT IPh IE L BLOCK2 OUTPUT...

Страница 320: ...EDs RemTrip L REMOTE TRIPPING PulseBLOUT1 OFF PulseBLIN1 OFF Relays PulseBLIN1 K LEDs PulseBLIN1 L PILOTE WIRE DIAGNOSTIC Test state OFF Stop test Yes Start test Yes Test KC1 1 Yes Test KC1 2 Yes Test...

Страница 321: ...control of self test undetectable failures comparing of measures with the external instruments auxiliary voltage control etc analysis of the stored information faults and events and oscillographic re...

Страница 322: ...Minimum power factor 59 Overvoltage U 6 59N Residual overvoltage UE 6 59V2 Negative sequence overvoltage 64REF Low impedance restricted earth fault 66 Maximum number of startings 67N Ground directiona...

Страница 323: ...or all inverse time characteristics following data applies Asymptotic reference value minimum pickup value 1 1 I inv Minimum operate time 0 1 s Range where the equation is valid 2 3 1 1 I I inv 20 If...

Страница 324: ...nverse time curve type A F_46M IECA Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I2 I2 inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s t2 inv 5 s 1 s 0 5 s 0 2 s 0 1 s 0 02 s t t2 inv I2 I2 inv 0 02 1 0 14 Note m...

Страница 325: ...ve IEC 60255 3 BS142 type B F_46B IECB Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I2 I2 inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s t2 inv 5 s 1 s 0 5 s 0 2 s t inv 0 02 s t inv 0 1 s t t2 inv I2 I2 inv 1 1...

Страница 326: ...60255 3 BS142 type C F_46M IECC Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I2 I2 inv 0 01 0 1 1 10 100 1000 10000 100000 t s 10 s 60 s t2 inv 5 s 1 s t2 inv 0 5 s t2 inv 0 2 s t2 inv 0 02 s t2 inv 0 1 s t t i...

Страница 327: ...2 type A F_51 IECA Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I I H inv I I L inv 0 01 0 1 1 10 100 1000 10000 t s 10 s t H inv 60 s 5 s 1 s 0 5 s 0 2 s 0 1 s 0 02 s t t H inv I I H inv 0 02 1 0 14 t t L inv I...

Страница 328: ...type B F_51 IECB Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I I H inv I I L inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 02 s 0 1 s Nota il tempo d intervento impostato riferito ad un v...

Страница 329: ...ype B F_51N IEC LITB Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I I H inv I I L inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 02 s 0 1 s t t H inv t H inv I I H inv 1 120 t t L inv t L i...

Страница 330: ...type C F_51 IECC Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I I H inv I I L inv 0 01 0 1 1 10 100 1000 10000 100000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 02 s 0 1 s t t H inv t H inv t L inv I I H inv 2 1 80 t...

Страница 331: ...har ai 1 1 2 3 4 5 6 7 8 9 10 20 IE1 IE1 inv IE2 IE2 inv IEC IEC inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 1 s 0 02 s t tE1 inv IE1 IE1 inv 0 02 1 0 14 t tE2 inv IE2 IE2 inv...

Страница 332: ...CB Char ai 1 1 2 3 4 5 6 7 8 9 10 20 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 02 s 0 1 s t tE1 inv IE1 IE1 inv 1 13 5 t tE2 inv IE2 IE2 inv 1 13 5 Note match of operating and s...

Страница 333: ...LITB Char ai Note match of operating and setting time takes place when IE1 IE1 inv IE2 IE2 inv o IEC IEC inv 121 1 1 2 3 4 5 6 7 8 9 10 20 0 01 0 1 1 10 100 1000 10000 t s I E1 IE1 inv I E2 IE2 inv I...

Страница 334: ...C Char ai 1 1 2 3 4 5 6 7 8 9 10 20 0 01 0 1 1 10 100 1000 10000 100000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 02 s 0 1 s t tE1 inv IE1 IE1 inv 2 1 80 t tE2 inv IE2 IE2 inv 2 1 80 Note match of operating...

Страница 335: ...10 100 1000 10000 t s tED inv 10 s tED inv 10 s tED inv 60 s tED inv 60 s tPD inv 5 s tED inv 5 s tED inv 1 s tED inv 1 s tED inv 0 5 s tED inv 0 5 s tED inv 0 2 s tED inv 0 2 s tED inv 0 1 s tED inv...

Страница 336: ...inv 5 s tED inv 5 s tED inv 1 s tED inv 1 s tED inv 0 5 s tED inv 0 5 s tED inv 0 2 s tED inv 0 2 s tED inv 0 02 s tED inv 0 02 s tED inv 0 1 s tED inv 0 1 s Note match of operating and setting time...

Страница 337: ...01 0 1 1 10 100 1000 10000 100000 t s tED inv 10 s tED inv 10 s tED inv 60 s tED inv 60 s tED inv 5 s tED inv 5 s tED inv 1 s tED inv 1 s tED inv 0 5 s tED inv 0 5 s tED inv 0 2 s tED inv 0 2 s tED in...

Страница 338: ...e A F_51 IECA Char ai 1 1 2 3 4 5 6 7 8 9 10 20 IECH IEDC inv IECL IEDC inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 1 s 0 02 s tEDC inv Note match of operating and setting tim...

Страница 339: ...e B F_67N Comp IECB Char ai 1 1 2 3 4 5 6 7 8 9 10 20 IECL IEDC inv IECH IEDC inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 02 s 0 1 s Note match of operating and setting time t...

Страница 340: ...0 s 5 s 1 s 0 5 s 0 2 s 0 02 s 0 1 s Nota il tempo d intervento impostato riferito ad un valore di corrente pari a IECL IEDC inv o IECH IEDC inv 9 F_67N Comp IECBC Char ai tEDC inv t tEDC inv IECH IED...

Страница 341: ...ve L 0 024 for ANSI IEEE Extremely inverse curve For all inverse time characteristics following data applies Asymptotic reference value minimum pickup value 1 1 I inv Minimum operate time 0 1 s Range...

Страница 342: ...e ANSI IEEE type MI F_46LT ANSIMI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I2 I2 inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s t2 inv 5 s 1 s t2 inv 0 02 s t2 inv 0 2 s t2 inv 0 1 s t2 inv 0 5 s t t2 inv I2...

Страница 343: ...ANSI IEEE type VI F_46LT ANSIVI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I2 I2 inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s t2 inv 5 s 1 s t2 inv 0 5 s t2 inv 0 2 s t2 inv 0 1 s t2 inv 0 02 s t t2 inv I2 I...

Страница 344: ...ANSI IEEE type EI F_46LT ANSIEI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I2 I2 inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s t2 inv 5 s t2 inv 0 5 s t2 inv 1 s t2 inv 0 2 s t2 inv 0 1 s t2 inv 0 02 s t t2 i...

Страница 345: ...MI F_51 ANSIMI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I I H inv I I L inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 02 s 0 2 s 0 1 s 0 5 s t t H inv t H inv t L inv I I H inv 0 02 1 0 01 0 023...

Страница 346: ...VI F_51 ANSIVI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 1 s 0 02 s t t H inv I I H inv 2 1 3 922 0 092 t t L inv I I L inv 2 1 3 922 0 092 Not...

Страница 347: ...pe EI F_51 ANSIEI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 0 5 s 1 s 0 2 s 0 1 s 0 02 s t t H inv I I H inv 2 1 5 64 0 024 t t L inv I I L inv 2 1 5 64 0 024 No...

Страница 348: ...3 4 5 6 7 8 9 10 20 IE1 IE1 inv IE2 IE2 inv IEC IEC inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 02 s 0 2 s 0 1 s 0 5 s t tE1 inv IE1 IE1 inv 0 02 1 0 01 0 023 t tE2 inv IE2 IE2 inv 0 02 1...

Страница 349: ...3 4 5 6 7 8 9 10 20 IE1 IE1 inv IE2 IE2 inv IEC IEC inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 1 s 0 02 s t tE1 inv IE1 IE1 inv 2 1 3 922 0 092 t tE2 inv IE2 IE2 inv 2 1 3 9...

Страница 350: ...5 6 7 8 9 10 20 IE1 IE1 inv IE2 IE2 inv IEC IEC inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 0 5 s 1 s 0 2 s 0 1 s 0 02 s t tE1 inv IE1 IE1 inv 2 1 5 64 0 024 t tE2 inv IE2 IE2 inv 2 1 5 64 0 0...

Страница 351: ...I IEEE type MI F_67N ANSIMI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 IED IED inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s tED inv 5 s 1 s tED inv 0 02 s tED inv 0 2 s tED inv 0 1 s tED inv 0 5 s t tED inv...

Страница 352: ...IEEE type VI F_67N ANSIVI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 IED IED inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s tED inv 5 s 1 s tED inv 0 5 s tED inv 0 2 s tED inv 0 1 s tED inv 0 02 s t tED inv IE...

Страница 353: ...EEE type EI F_67N ANSIEI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 IED IED inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s tED inv 5 s tED inv 0 5 s tED inv 1 s tED inv 0 2 s tED inv 0 1 s tED inv 0 02 s t tED...

Страница 354: ...NSIMI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 02 s 0 2 s 0 5 s 0 1 s Note match of operating and setting time takes place when IEDH IEDC inv or IEDL IEDC...

Страница 355: ...ANSIVI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 1 s 0 5 s 0 2 s 0 1 s 0 02 s Note match of operating and setting time takes place when IEDH IEDC inv or IEDL IED...

Страница 356: ...Comp ANSIEI Char ai 1 1 2 3 4 5 6 7 8 9 10 20 IPD IPD inv IPD IPD inv 0 01 0 1 1 10 100 1000 10000 t s 10 s 60 s 5 s 0 5 s 1 s 0 2 s 0 1 s 0 02 s Note match of operating and setting time takes place...

Страница 357: ...for I squared t I2t curve B 0 339 for Electromechanical curve EM For all inverse time characteristics following data applies Asymptotic reference value minimum pickup value 1 1 I inv Minimum operate...

Страница 358: ...ar ai 0 01 0 1 1 100 10 1000 10 000 100 000 1000 000 t s 1 1 2 3 4 5 6 7 8 9 10 20 I I L inv I I H inv 60 s 10 s 5 s 1 s 0 1 s 0 5 s 0 02 s 0 1 s t t H inv t H inv t L inv I I H inv 5 6 1 2351 t t L i...

Страница 359: ...6M I2t Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I2 I2 inv 0 01 0 1 1 10 100 1000 10000 t s t2 inv 60 s t2 inv 10 s t2 inv 10 s t2 inv 5 s t2 inv 5 s t2 inv 1 s t2 inv 0 5 s t2 inv 0 2 s t2 inv 0 1 s t2 inv 0...

Страница 360: ...I H inv I I H inv I I L inv I I L inv 0 01 0 1 1 10 100 1000 10000 t s 60 s 10 s 10 s 5 s 5 s 1 s 0 5 s 0 2 s t inv 0 1 s t inv 0 02 s t t H inv t H inv t L inv t H inv t L inv I I H inv 2 16 t t L in...

Страница 361: ...IPD IPD inv IPD IPD inv tPD inv 1 s tPD inv 1 s tPD inv 0 5 s tPD inv 0 5 s tPD inv 0 2 s tPD inv 0 2 s tPD inv 0 1 s tPD inv 0 1 s tPD inv 0 02 s tPD inv 0 02 s tPD inv 10 s tPD inv 10 s tPD inv 5 s...

Страница 362: ...anical inverse curves EM F_46LT EM Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I2 I2 inv 0 01 0 1 1 10 100 1000 10000 t s 60 s t2 inv 10 s 5 s 1 s 0 5 s 0 2 s t2 inv 0 1 s t2 inv 0 02 s Note match of operating...

Страница 363: ...F_51 EM Char ai 1 1 2 3 4 5 6 7 8 9 10 20 I I L inv I I H inv 0 01 0 1 1 10 100 1000 10000 t s 60 s 10 s 5 s 1 s 0 5 s 0 2 s 0 1 s 0 02 s Note match of operating and setting time takes place when I I...

Страница 364: ...curves EM F_51N EM Char ai 1 1 2 3 4 5 6 7 8 9 10 20 IE IE inv 0 01 0 1 1 10 100 1000 10000 t s 60 s 10 s 5 s 1 s 0 5 s 0 2 s 0 1 s 0 02 s Note match of operating and setting time takes place when IE...

Страница 365: ...har ai 1 1 2 3 4 5 6 7 8 9 10 20 0 01 0 1 1 10 100 1000 10000 t s IED IED inv IED IED inv 0 1 s 0 02 s 10 s 5 s 1 s 0 5 s 0 2 s 60 s tED inv tED inv Note match of operating and setting time takes plac...

Страница 366: ...s IEDC IEDH inv IEDC IEDH inv IEDC IEDL inv IEDC IEDL inv 0 1 s 0 02 s 10 s 5 s 1 s 0 5 s 0 2 s 60 s Note match of operating and setting time takes place when IEDC IEDH inv 4 or IEDC IEDH inv 4 t tEDC...

Страница 367: ...GND4 GND5 GND6 GND7 GND8 GND1 MPT2 T2 7 8 9 PT3 MPT3 T3 10 11 12 PT4 MPT4 T4 13 14 15 PT5 MPT5 T5 16 17 18 PT6 MPT6 T6 19 20 21 PT7 MPT7 T7 22 23 24 PT8 MPT8 T8 IRIG B AM IRIG B IN IRIG B 1PPS IN 1PPS...

Страница 368: ...PANEL Supervision unit 5 6 RS485 A B X TX 1 TX 1 ETHERNET TX 1 FX 1 ETHERNET FX 1 FX 1 ETHERNET Note 1 two redundant ports with hw sw switching selectable from TX RJ45 FX optical ber TX TX or FX FX A...

Страница 369: ...ber of startings Restart inhibition 67N Ground directional overcurrent 67N Comp Ground directional overcurrent with calculated residual current 81O 81U Overfrequency and underfrequency 87G 87M 87T Dou...

Страница 370: ...1N Comp 50N 1 51N 2 87NHIZ 50N 1 51N 1 59N 67N 67N Comp 74VT 74CT IL1L IL2L IL3L A2 A3 A4 A5 A6 A7 A8 IE1 B9 B10 dn da dn db dn dc Antiferrorisonance Differential protection of generator NOTE To curre...

Страница 371: ...nce terminals of of the relay current inputs are considered positive the outgoing negative This convention applies to indicate the P1 CTs polarity toward the protected transformer L1 L2 L3 P1 S1 S2 P2...

Страница 372: ...n db dn dc Antiferrorisonance Differential protection of Transformer generator NOTE To current with incoming direction in the protected component must match incoming current in the reference terminals...

Страница 373: ...ntion applies to indicate the P1 CTs polarity toward the protected transformer Note when 87NHIZ is enabled the 50N 51N 67N functions can not be used with residual current IE measured directly NVA100X...

Страница 374: ...UNTING CUTOUT SIDE VIEW REAR VIEW FRONT VIEW 177 215 222 20 210 0 3 164 4 158 0 0 3 189 94 5 N 4 holes 4 2 RACK MOUNTING N 4 holes 4 2 156 164 4 177 207 189 215 IN2D IN1C OC1E OC2F NVA100 DX MM00 In 5...

Страница 375: ...3 6 9 ThySetter 3 6 9 ThySetter 3 6 11 ThySetter 3 6 11 ThySetter 3 6 13 ThySetter 3 6 13 04 2014 06 2014 01 2015 02 2015 03 2016 04 2016 First edition 24 element and PLC removed Correction on par 4...

Страница 376: ...Directive EMC Directive Reference of standards and or technical speci cations applied for this declaration of conformity or parts thereof harmonized standards Reference n issue title EN 61010 1 EN 50...

Отзывы:

Нет отзывов

Бренды по названию

Популярные бренды

Загрузить еще бренды