56
••••
LAI theory
Document code: SS1-UM-1.05
Beer's law for canopy absorption
Beer's law occurs in many situations where events happen at random. In the case of
light absorption by a canopy, it applies to the absorption of incident photons or light
rays. For a uniform infinite randomly distributed canopy of completely absorbing
leaves, it can be shown that the relationship between the transmitted light
I,
a beam
of incident light
I
0
and the Leaf Area Index
L
is given by:
I
.
I 0 exp(
)
.
K L
where
K
is the extinction coefficient which depends on the leaf angle distribution
and the direction of the beam.
K
=1 for entirely horizontal leaves.
Campbell's Ellipsoidal LAD equations.
Campbell (1986) derives an equation for the extinction coefficient of leaves
distributed in the same proportions and orientation as the surface of an ellipsoid of
revolution, symmetrical about a vertical axis. The semi vertical axis is
a
and the semi
horizontal axis is
b
. There is symmetry about the vertical axis. He relates these to a
single parameter
x = b/a
. (
x
is the Ellipsoidal Leaf Angle Distribution Parameter, or
ELADP). The extinction coefficient also depends on the zenith angle of the
incoming direct beam. Canopy elements are assumed to be completely black, and
randomly distributed in a horizontal slab extending to infinity in all directions.
Note: in the following equations derived in MathCad, different conventions are used
for some symbols. Equality is represented by
:
=, and tan
2
(
θ
) is expressed tan(
θ
)
2
.
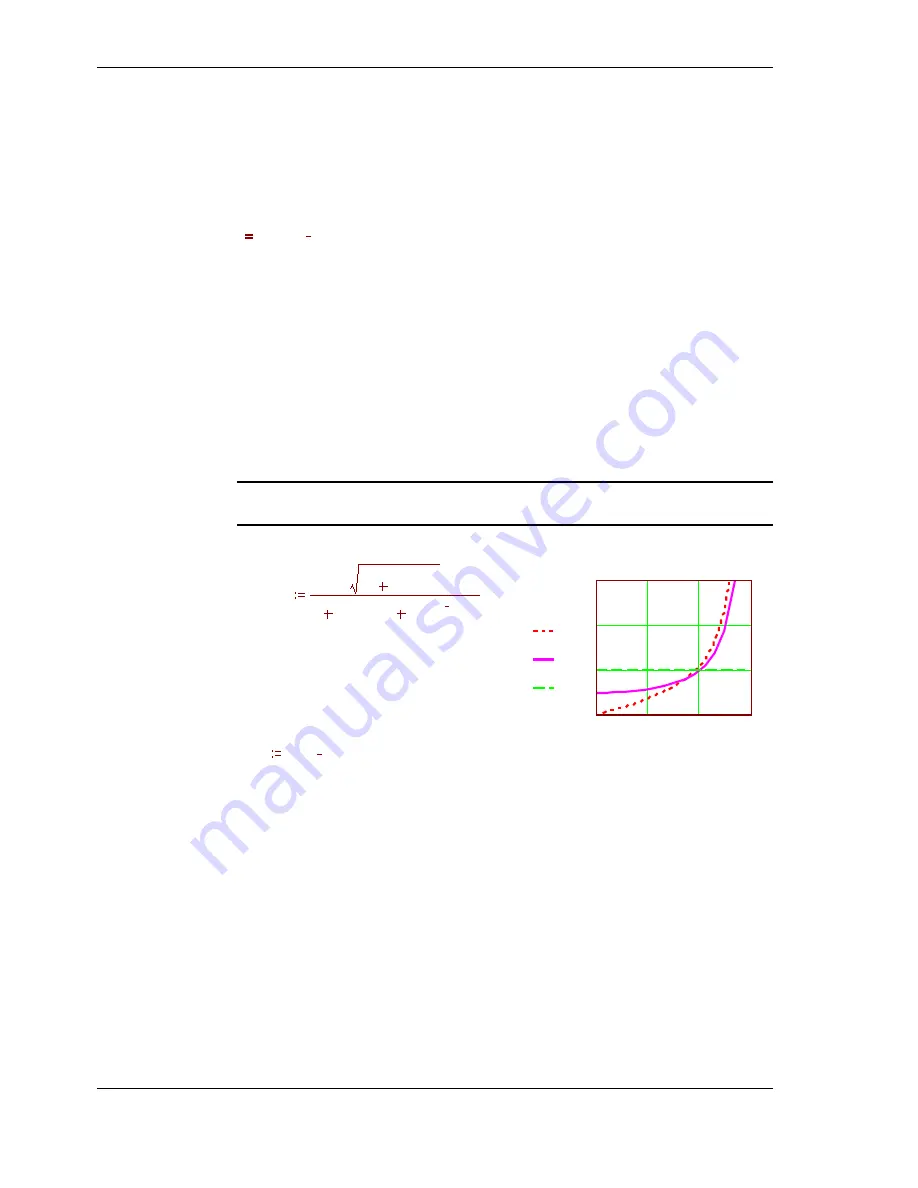
The extinction coefficient,
K
, is calculated as follows:
Where:
x
is the ELADP
θθθθ
is the zenith angle of the direct
beam.
The transmitted fraction of incident
direct light is given by:
τ
dir
exp(
)
.
K (
)
,
x
θ
L
where
L
is the canopy LAI.
Transmission of Diffuse Light
Campbell's analysis applies only to a beam of light from a specific direction, which
is the Direct solar beam in our case. Even under strong sunlight, the Direct fraction
rarely exceeds 80% of the Total incident radiation, so penetration of the Diffuse
component of incident radiation is also important.
There is a misconception that the extinction coefficient for Diffuse light is
independent of canopy Leaf Angle Distribution, but this is not the case as the
following analysis shows. As the following graph also shows, transmission of
Diffuse light does not obey a simple Beer's law curve, so cannot be represented by a
single extinction coefficient, except in the case of a horizontal LAD.
0
1
2
3
K(
)
,
0
θ
K(
)
,
1
θ
K(
)
,
100
θ
θ
K (
)
,
x
θ
x
2
tan( )
θ
2
x
.
1.702 (
)
x
1.12
0.708
Ext'n
Coeff't
0
°
90
°
















































