Brookfield Engineering Labs., Inc.
Page 82
Manual No. M13-167-A0415
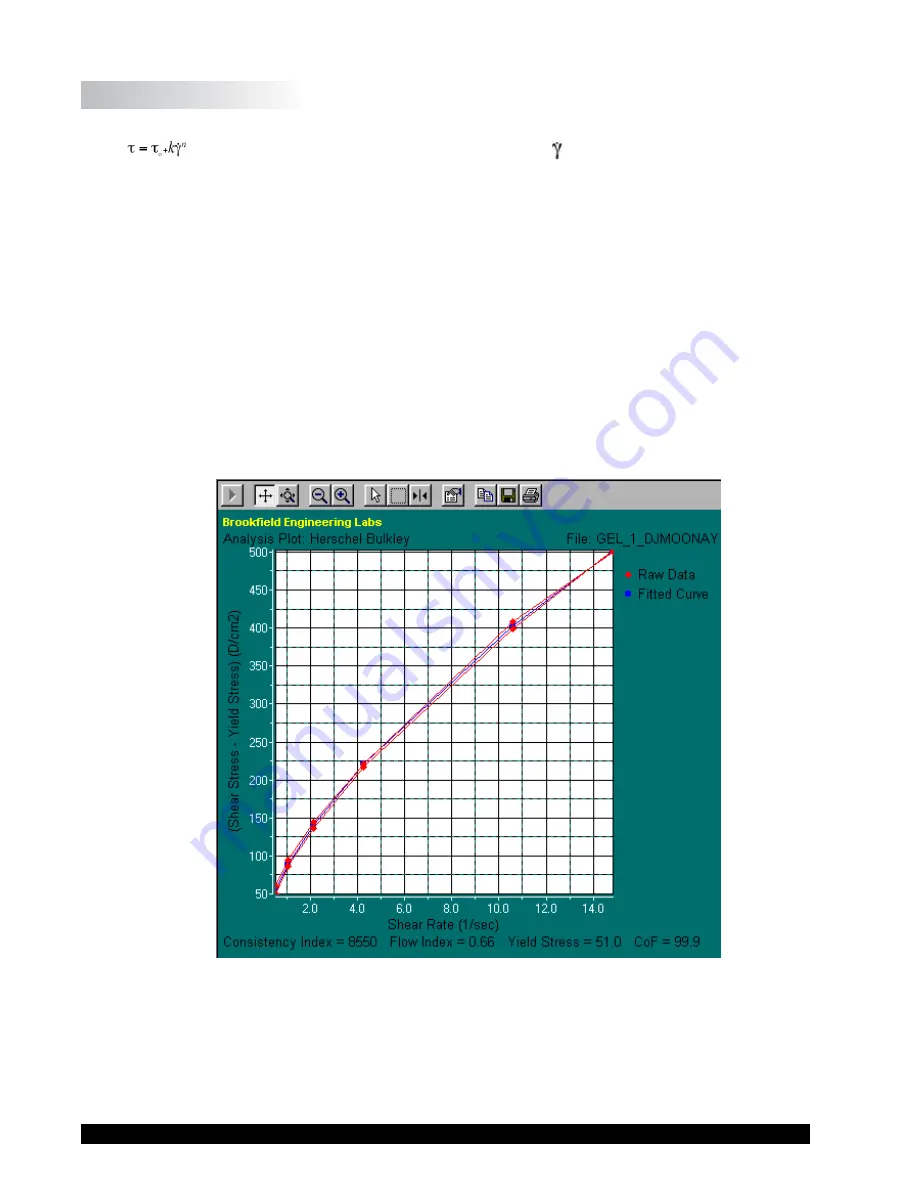
VII.2 The Herschel-Bulkley Model
(
τ
= shear stress,
τ
o
= yield stress,
k
= consistency index,
= shear rate, and
n
= flow index)
What does it tell you?
The Herschel-Bulkley model is simply the Power Law model with the addition of
τ
o
for yield
stress. Yield stress,
τ
o
, denotes how much shear stress is required to initiate flow. This model also
provides a consistency index,
k
, which is a product’s viscosity at 1 reciprocal second, and a flow
index,
n
, which indicates the degree with which a material exhibits non-Newtonian flow behavior.
Since Newtonian materials have linear shear stress vs. shear rate behavior and
n
describes the
degree of non-Newtonian flow, the flow index essentially indicates how “non-linear” a material
is. For Herschel-Bulkley fluids,
n
will always be greater than or less than 1.
When
n
< 1 the product is shear-thinning or Pseudoplastic. This means the apparent viscosity
decreases as shear rate increases. The closer
n
is to 0, the more shear thinning the material is.
When
n
> 1 the product is shear-thickening or Dilatant. It’s apparent viscosity increases as shear
rate increases.
VII-2
When should you use it?
The Herschel-Bulkley model should be used with non-Newtonian, time-dependent materials that
have a yield stress. Products with a yield stress only begin to flow after a certain amount of shear
stress is applied. As a result, the flow curve intersects the y-axis at a point greater than 0. After
















































