XV
It is obvious that measurement results as a rule may
be associated with errors. This applies equally to
standardized methods of analysis (reference
methods) and to routine analysis. The discovery and
the minimization of errors must be the objective here.
A distinction is made between systematic errors and
random errors.
Systematic errors
are present when all the results of
an analysis deviate from the true value with the same
algebraic sign. Examples here include: a wrong sam-
ple volume, a wrong pH, a wrong reaction time, a
sample-matrix influence, etc. Systematic errors thus
affect the
accuracy
of the method of analysis.
Accuracy
= Deviation of the measured concentra-
tion from the true concentration
Random errors
manifest themselves in the form of a
wide range of deviation of the results of a given sam-
ple. These can be kept to a minimum by ensuring
good operating techniques and multiple determina-
tion with calculation of the mean values. Random
errors make the result of the analysis unreliable; they
influence the
precision
.
Precision =
Dispersion of the results among each
other
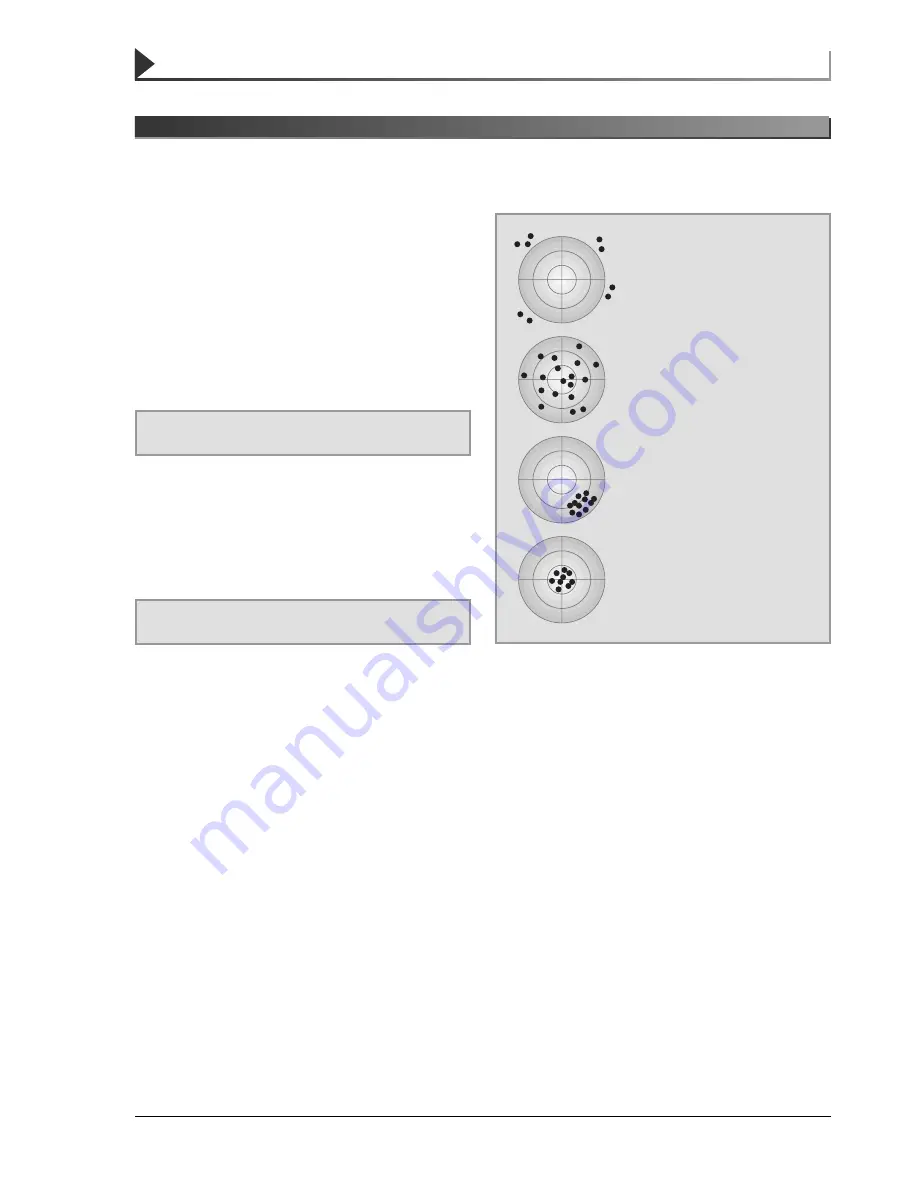
The following diagram illustrates the aspects of
accuracy and precision:
5.4 Definition of Errors
Accuracy: poor
Precision: poor
Major errors have been made!
Accuracy: good
Precision: poor
Calculation of the mean values
from at least three – or better
even more – parallel determina-
tions yields an approximation of
the true value.
Accuracy: poor
Precision: good
The high degree of precision mis-
takenly indicates a correct value!
Accuracy: good
Precision: good
The ideal objective!
5. Analytical Quality Assurance (AQA)
Release 07/03
















































