28
G
ETTING
S
TARTED WITH THE
CBR 2™
S
ONIC
M
OTION
D
ETECTOR
©
1997,
2004,
2006
T
EXAS
I
NSTRUMENTS
I
NCORPORATED
Activity 5—Rolling Ball
Notes for Teachers
Concepts
Function explored: parabolic
Plotting a ball rolling down a ramp of varying
inclines creates a family of curves, which can be
modeled by a series of quadratic equations. This
activity investigates the values of the coefficients in
the quadratic equation,
y
=
ax
2
+
bx
+
c
.
Materials
Ÿ
calculator (see page 2 for available models)
Ÿ
CBR 2™ motion detector
Ÿ
unit-to-CBR 2™ or I/O unit-to-unit cable
Ÿ
EasyData application or RANGER program
Ÿ
large (9 inch) playground ball
Ÿ
long ramp (at least 2 meters or 6 feet—a
lightweight board works well)
Ÿ
protractor to measure angles
Ÿ
books to prop up ramp
Ÿ
TI ViewScreen
é
panel (optional)
Hints
Discuss how to measure the angle of the ramp. Let
students get creative here in measuring the initial
angle. For example, they might use a trigonometric
calculation or folded paper.
For steeper angles (greater than 60º), you may
want to use a CBR 2™ motion detector clamp (sold
separately).
See pages 6–9 for hints on effective data collection.
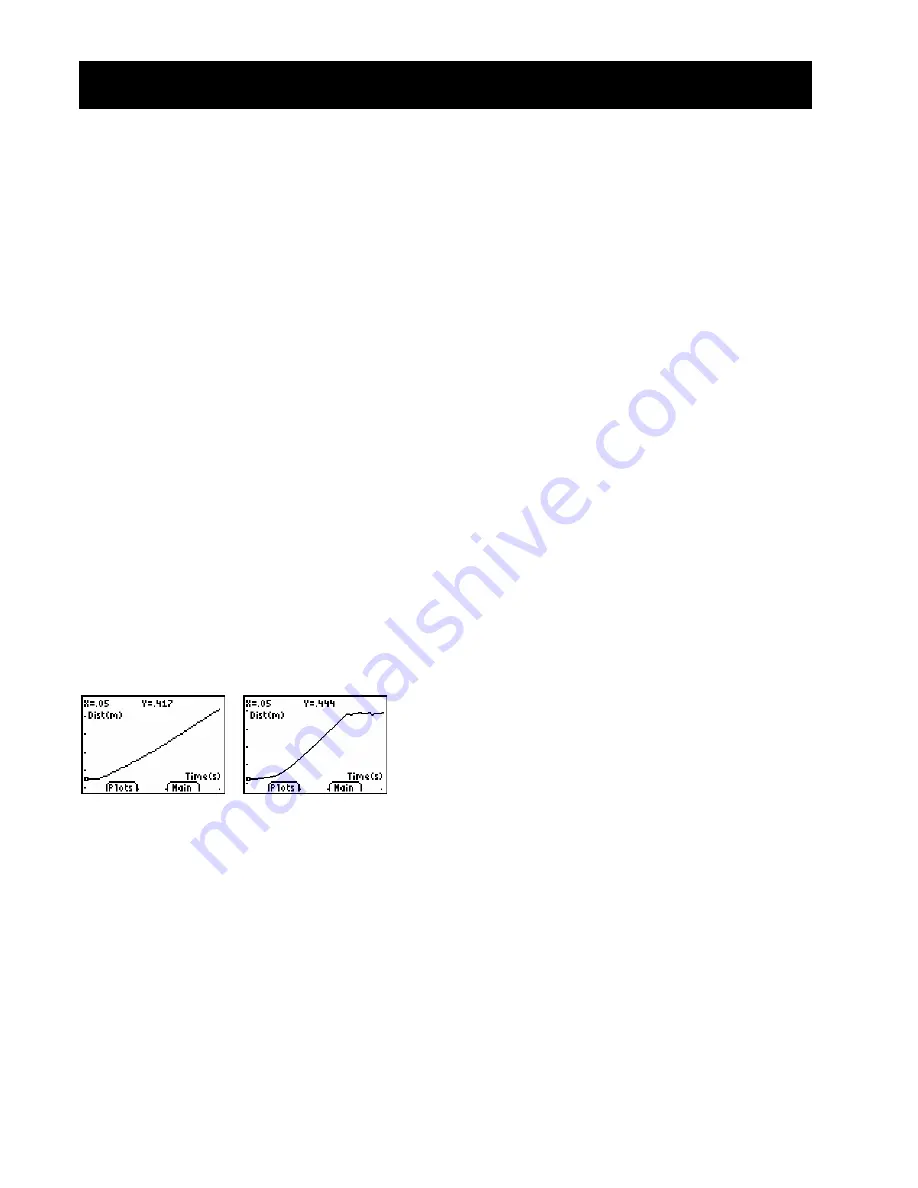
Typical plots
15
¡
30
¡
Typical answers
1. the third plot
2. time; seconds; distance of object from CBR 2™
motion detector; feet or meters
3. varies (should be half of a parabola, concave
up)
4. a parabola (quadratic)
5. varies
6. varies (should be parabolic with increasing
curvature)
7. 0
¡
is flat (ball can’t roll); 90
¡
is the same as a
free-falling (dropping) ball
Explorations
The motion of a body acted upon only by gravity is
a popular topic in a study of physical sciences. Such
motion is typically expressed by a particular form of
the quadratic equation,
s
= ½
at
2
+
v
i
t
+
s
i
where
0
s
is the position of an object at time
t
0
a
is its acceleration
0
v
i
is its initial velocity
0
s
i
is its initial position
In the quadratic equation
y
=
ax
2
+
bx
+
c
,
y
represents the distance from the
CBR 2™
motion
detector to the ball at time
x
if the ball’s initial
position was
c
, initial velocity was
b
, and
acceleration is 2
a
.
Advanced explorations:
Since the ball is at rest when released,
b
should
approach zero for each trial.
c
should approach the
initial distance, 0.5 meters (1.5 feet).
a
increases as
the angle of inclination increases.
If students model the equation
y
=
ax
2
+
bx
+
c
manually, you may need to provide hints for the
values of
b
and
c
. You may also direct them to
perform a quadratic regression on lists
L1
,
L2
using
their calculators. The ball’s acceleration is due to
the earth’s gravity. So the more the ramp points
down (the greater the angle of inclination), the
greater the value of
a
. Maximum
a
occurs for
q
= 90
¡
, minimum for
q
= 0
¡
. In fact,
a
is
proportional to the sine of
q
.






























