Galil DMC-1510, User Manual

Page: 153 / 203

DMC-1500 Chapter 10 Theory of Operation
•
141
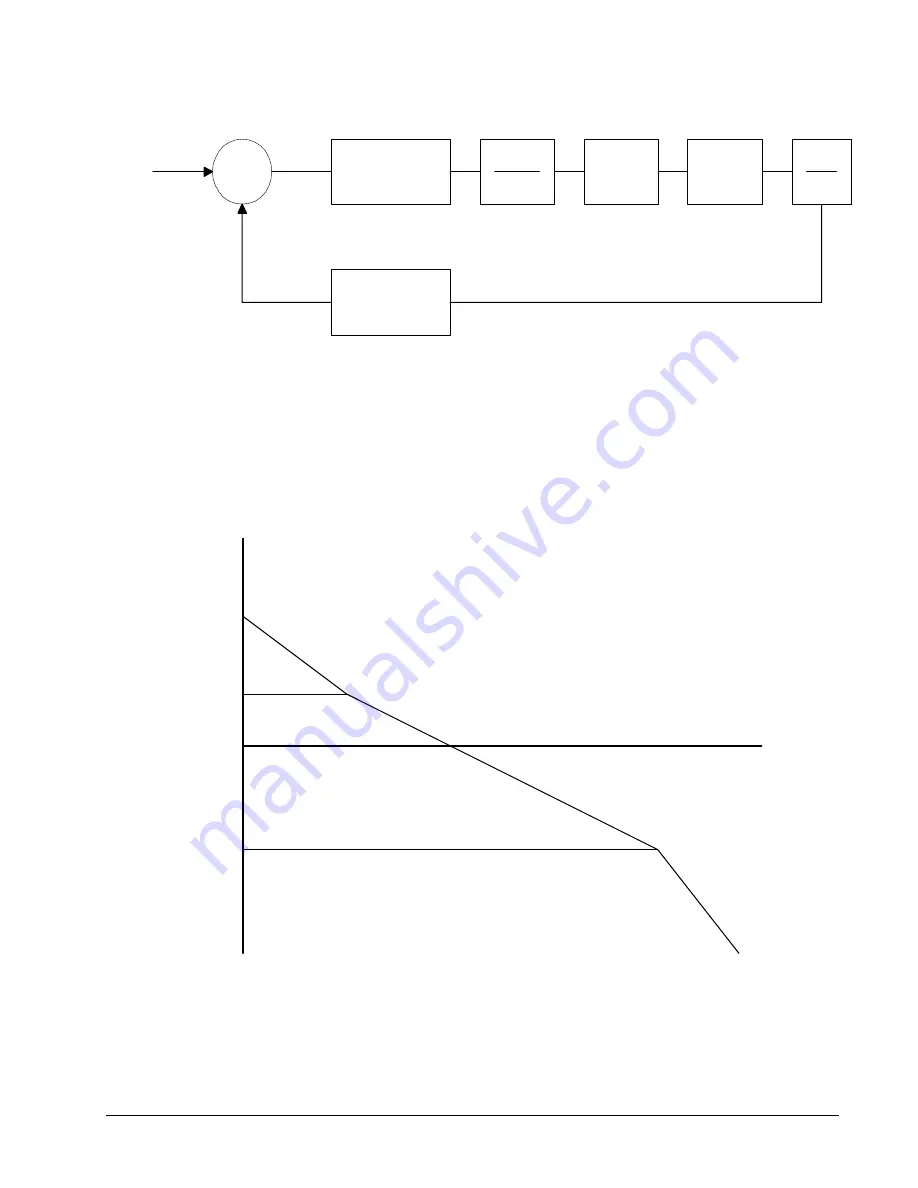
Figure 10.7 - Mathematical model of the control system
The open loop transfer function, A(s), is the product of all the elements in the loop.
A = 390,000 (s+51)/[s2(s+2000)]
To analyze the system stability, determine the crossover frequency,
ω
c at which A(j
ω
c)
equals one. This can be done by the Bode plot of A(j
ω
c), as shown in Fig. 10.8.
Figure 10.8 - Bode plot of the open loop transfer function
For the given example, the crossover frequency was computed numerically resulting in 200 rad/s.
Next, we determine the phase of A(s) at the crossover frequency.
A(j200) = 390,000 (j200+51)/[(j200)2 . (j200 + 2000)]
Σ
50+0.980s
318
V
ENCODER
500
S
2
FILTER
2000
S+2000
0.0003 4
ZOH DAC
AMP
MOTOR
1
4
0.1
50 200 2000 W (rad/s)
Magnitude