35
The Lambert-Beer law applies over a wide range of concentrations and particles and thus is useful to get
an overall picture of the particle mass flow. Thus, opacity sensors have a high sensitivity to changes in
this range. However, opacity sensors are known to be less accurate when there is a lot of light scattering
within the sample and when the particles are very small. To counter these issues, parSYNC® has included
a scattering sensor (sensitive to larger particles and when large amounts of scattering occur) plus an
ionization sensor (sensitive to ultra-fine particles).
7.4.2
Scattering
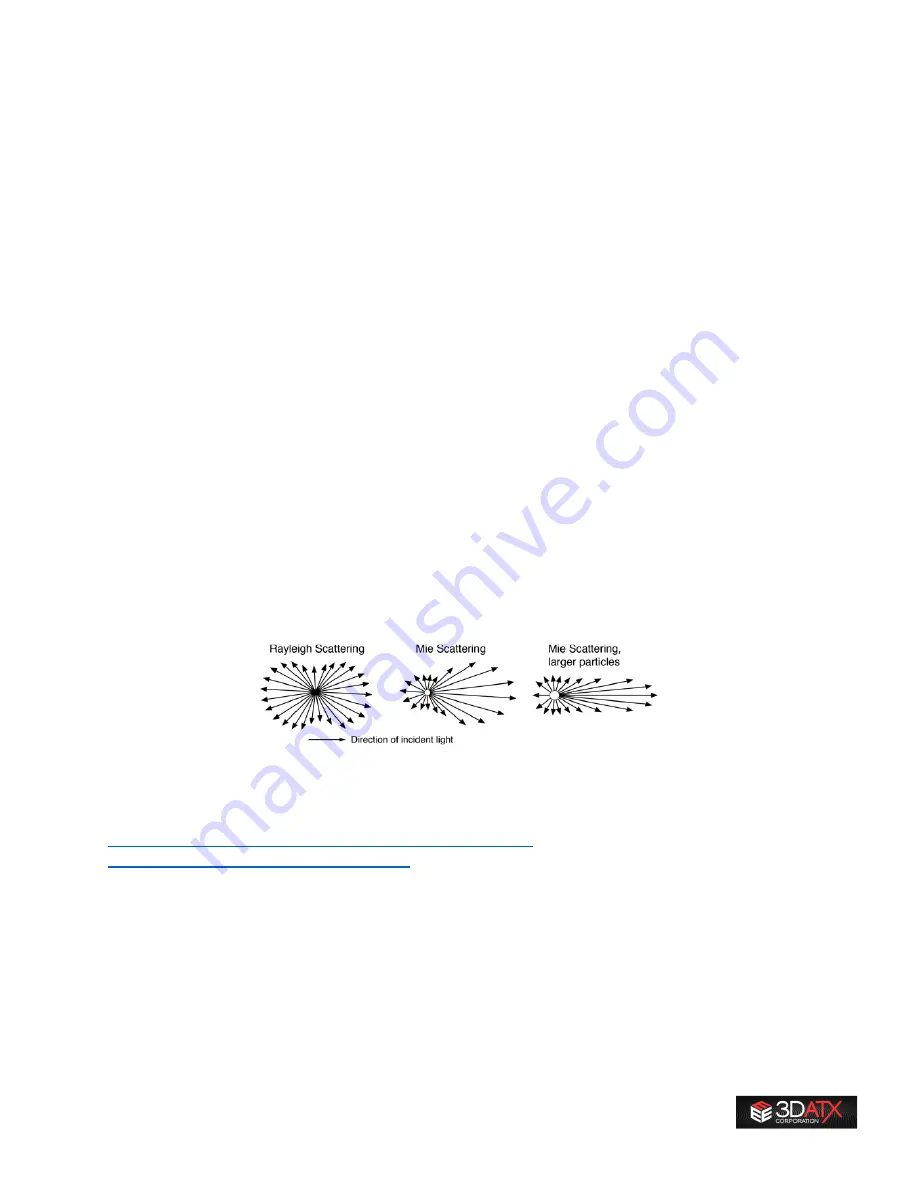
A greater number of particles will result in a greater amount of scattering; different sized particles along
with greater number of particles will affect the scattering profile, which in turn varies by angle.
For non-absorbing particles, a long derivation gives the following complicated formula for scattering
sensor’s response to the incoming light for Rayleigh scattering:
I / I
0
= (π
4
/ 8) * ((n
2
– 1) / (n
2
+ 2))
2
* (D
6
/ (r
2
* λ
4
)) * (1 + cos
2
θ)
n = index of refraction
D = particle diameter
r = distance of particle from light source
λ = wavelength of incident light
θ = scattering angle
Experimental data show that for comparatively uniform particle geometry and particle mass, the mass
concentration versus scattering is log-linear in the Rayleigh region. Hence, the electronics within a
scattering sensor can convert its readings to a usable output. It is well-known that the scattering sensors
are most sensitive with larger particles, as you might expect from the 6th power on the D factor in the
above formula.
For large particles, we are in the geometric scattering region. The equation is modelled with an
inhomogeneous wave equation with dissipation, as in:
https://omlc.org/software/mie/maetzlermie/Maetzler2002.pdf
http://www.thermopedia.com/content/158/
https://cims.nyu.edu/~corona/hw/nlgonotes.pdf
u
tt
–
Δu
– r
2
u = f(x, t)
with the appropriate initial and boundary conditions. This has known closed-form fundamental solutions
of the form
e
kx
(A(x, t) cos(ωt) + C(x, t) sin (ωt))
Summary of Contents for parSYNC
Page 1: ...User Guide 3DATX Corp parSYNC miniPEMS Updated July 2020 ...
Page 21: ...21 ...
Page 38: ...38 ...




































