Sharp EL-9600, Руководство пользователя

Страница: 41 / 97

Consider another example. Suppose the length of the side of a triangle opposite
a 65° angle is 4 and another side is of length 12.
Find the measure of the angle opposite the side of length 12. Press CL to view
the variable list. Enter A = 65, x = 4, and y = 12. Position the cursor on B and
press 2ndF EXE to solve for the unknown angle. Since any angle of a triangle
is between 0° and 180°, enter these values for BEGIN and END.
Press 2ndF EXE and you will see that the graphs of the left- and right-hand
sides of the equation sin = sin do not intersect.
The message “No solution” in window is then displayed at the bottom of the
screen. If you get this message when using the Graphic Solver, you should
enter another BEGIN and/or END within which the Graphic Solver will search
for solutions. In this case, however, you have included from BEGIN to END all
possible values for the measure of angle B. Thus, there is no triangle that could
have the indicated measures.
You can algebraically confirm this fact by noticing that sin B = (Y sin A)/X= 3 sin
65° = 2.719 >1 which is of course, impossible.
The Law of Cosines is helpful in solving problems when the lengths of two sides
and the angle between those sides is known or when the lengths of all three sides
are known. This law says that the square of the length of any one side of a
triangle equals the sum of the squares of the lengths of the other two sides minus
twice the product of the lengths of the other two sides and the cosine of the
angle between those sides. That is, if x , y , and z are the lengths of the three sides
of a triangle and
θ
is the angle between the two sides of lengths x and y , then:
z
2
= x
2
+ y
2
– 2 xy cos
θ
Law of Sines and Law of Cosines/TRIGONOMETRY USING THE SHARP EL-9600 37
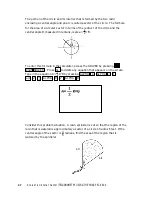
A
x
B
y