Sharp EL-9600, Руководство пользователя

Страница: 42 / 97

Access the SOLVER with 2ndF SOLVER (or press CL twice if you are still in
the SOLVER). Press CL to delete the current equation. Return to the Equation
Solver by pressing 2ndF SOLVER , touch A METHOD , and double touch
1 Equation . Next enter the Law of Cosines with the keystrokes:
ALPHA Z x
2
ALPHA = ALPHA X x
2
+ ALPHA Y x
2
–
2 ALPHA X
×
ALPHA Y
×
cos ALPHA
θ
Store this equation in the calculator using the method outlined to store the Law
of Sines.
Suppose you are given a triangle in which two sides of lengths 13 cm and 8 cm
enclose a 50° angle. Find the length of the third side of the triangle.
To find the solution using the Law of Cosines, press ENTER to view the list of
variables: Z, X, Y, and
θ
. Press
▼
to position the cursor on X and enter 13.
Next, enter 8 for Y and 50 for
θ
. Press
▲
to move the cursor over Z and press
0 ENTER . Press 2ndF EXE to solve for Z. Notice that the Equation Solver
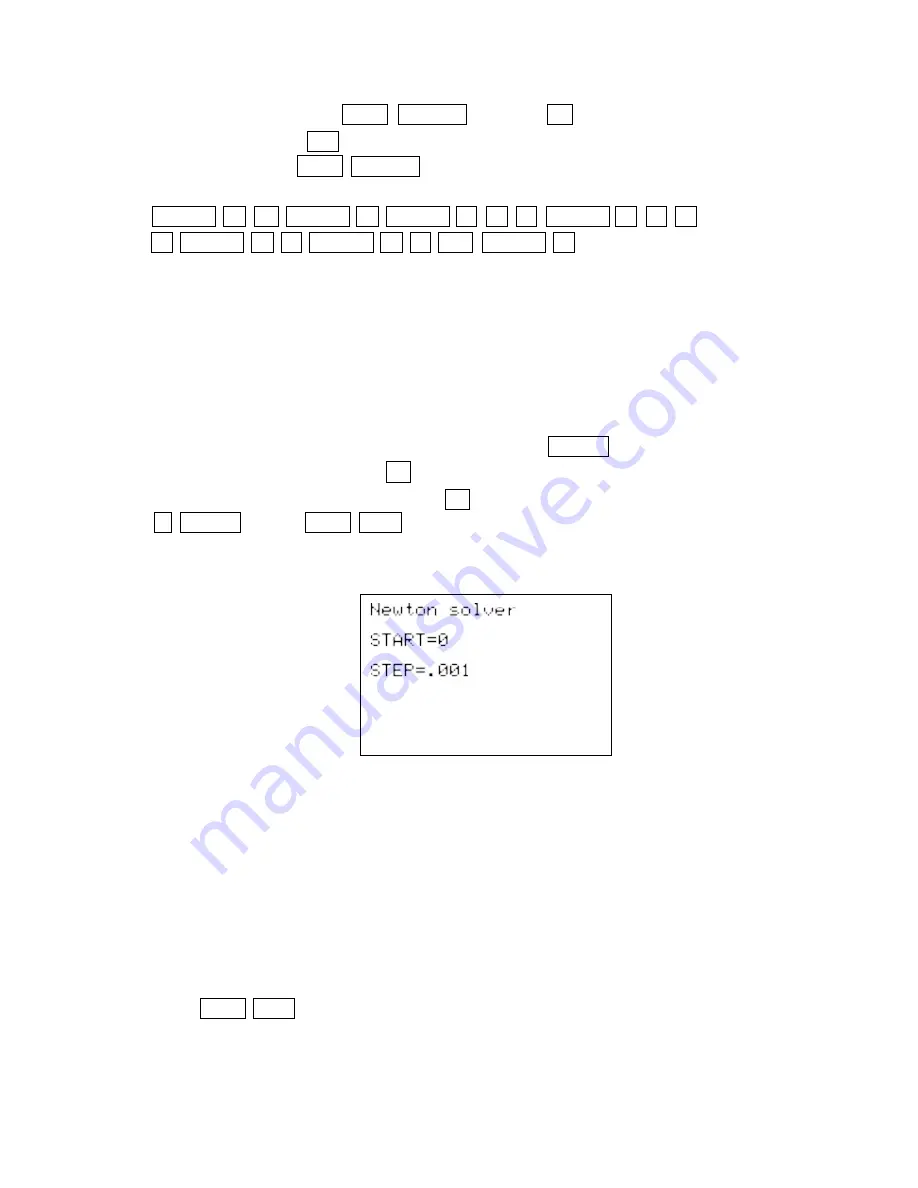
has automatically changed to the Newton Solver.
The calculator has chosen this method of solution since the equation is such
that a simple rearrangement of the variables will not produce a value for the
unknown. The Newton method uses iterations to approximate the root of the
equation. You should supply an initial estimate of the solution in the START
position (0 is the default value) and a step size STEP (.001 is the default value)
that the SOLVER uses to determine successive estimates.
Press 2ndF EXE to find the solution.
38 Law of Sines and Law of Cosines/TRIGONOMETRY USING THE SHARP EL-9600