PASCO ME-9502, Руководство пользователя

Страница: 54 / 94

S t a t i c s S y s t e m S i m p l e H a r m o n i c M o t i o n – B e a m o n a S p r i n g
®
50
012-12876B
Simple Harmonic Motion–Beam on a Spring
Imagine a horizontal beam that is supported by a hinge at one
end and a vertical spring at the other end. If the end of the
beam is pulled down, the spring exerts a restoring force,
F = -kx , to return the beam to its equilibrium position. The
beam will oscillate up and down with a period, T
beam
. For a
mass on a spring, the period, T , is as follows:
where M is the total oscillating mass and k is the spring constant. What is the period for a beam on a spring?
The beam rotates about the hinge as the end attached to the spring oscillates. The force of the spring on the oscil-
lating end of the beam,
F = -kx , produces a torque on the beam. Let L be the length of the lever arm of the beam.
The torque due to the spring is

= FL. A net torque causes angular acceleration,

, that is directly proportional to
the torque,

, and inversely proportional to the rotational inertia, I . That is,0,
or

=

I . Setting the two expressions for torque equal to each other gives FL =

I . Assume that the beam is like a
thin rod pivoted around one end. The rotational inertia of the thin rod is I = 1/3 m L
2
where m is the mass of the
beam. Since the force on the beam is F = -kx , the equation FL =

I becomes:
The angular acceleration,

, and the tangential (linear) acceleration, a
T
, of the oscillating end of the beam are
related. The tangential acceleration, a
T
=

r where r is the radius of rotation. In this case, the radius of rotation is
the lever arm, L, so a
T
=

L, or

= a
T
/L . The expression becomes:
which simplifies to
Solving for the tangential acceleration gives:
The tangential acceleration, a
T
= -

2
x, so the expression becomes:
Since the angular frequency,

= 2

/ T , the period, T = 2

/

or

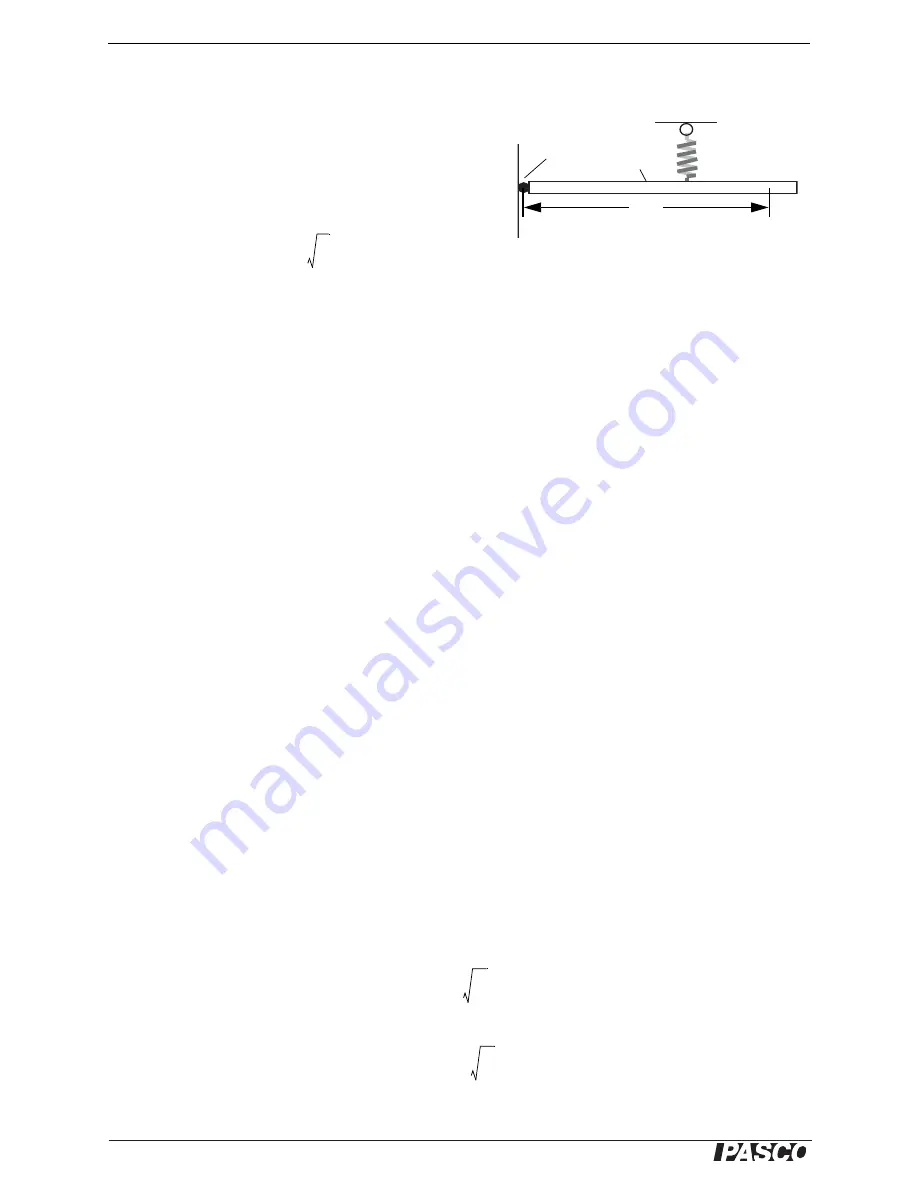
Hinge
Beam
Spring
L
Figure 9.3: Beam on a String
T
M
k
----- =


I
--
=
kxL –

mL
2
3
--------------
=
kxL –
a
T
mL
2
3 L
----------------
=
kx –
a
T
m
3
----------
=
a
T
3 k
m
------
x – =

2
x –
3 k
m
------
x – =

2
3 k
m
------
=

3 k
m
------ =
T 2

m
3 k
------ =