28
Rev. 1.0
0006302011
SSM23C User Manual
+86-400-820-9661
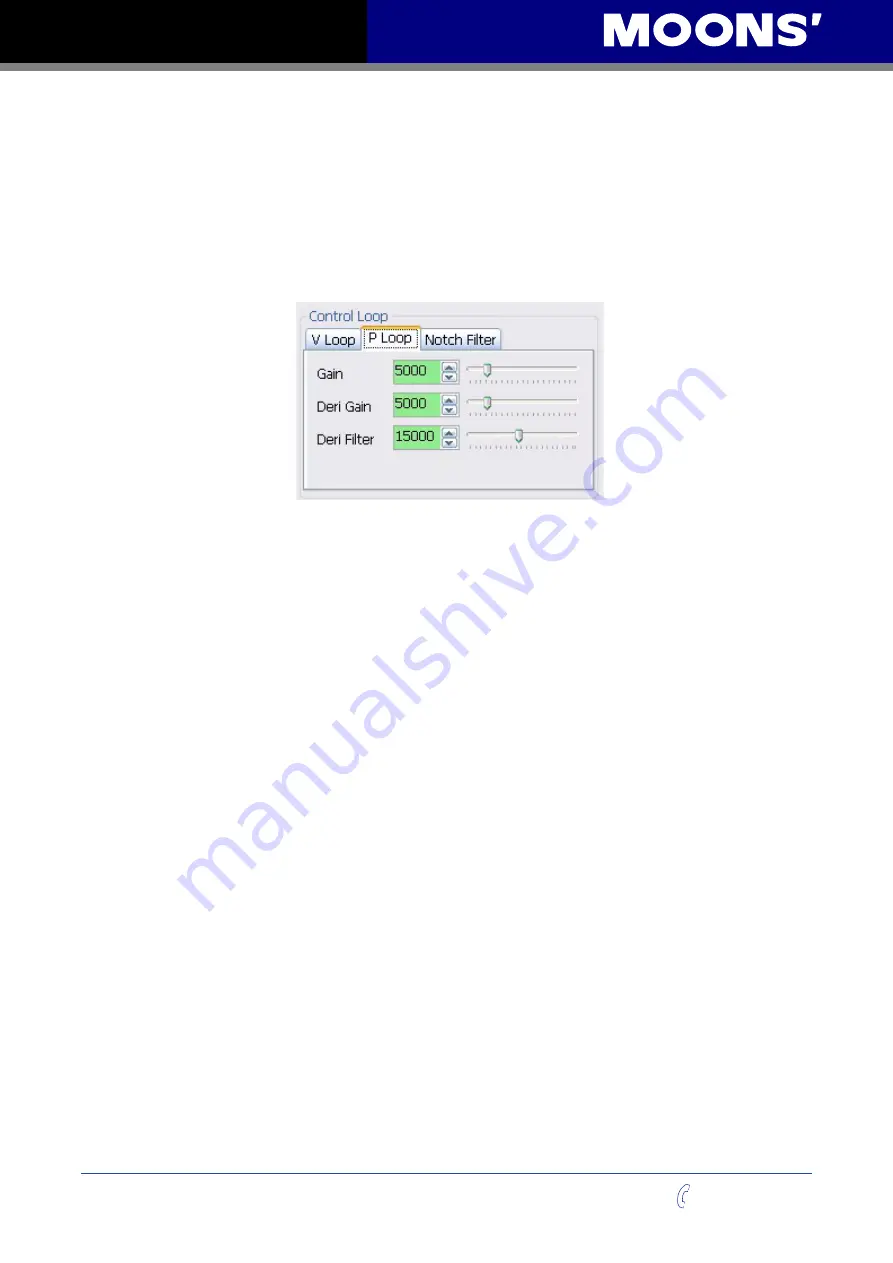
5.2 Position Control Loop
The
Position Control Loop
is designed to provide the typical positioning control for a servo
system. All positioning type operations use this loop including when operating in the
Pulse &
Direction Position Control Mode
. The Position loop can also be used in the
Velocity Control
Mode
when the
Position over time
control type option is selection or the Jog Mode is JM=1.
The Position Control Loop has three terms that can be configured for optimum performance with
the given load. These control terms are described below:
5.2.1 Gain: The Position Proportional Term (KP)
The simplest part of the Position loop is the proportional, or KP, term. The drive applies current
to the motor in direct proportion to the position error. For example, if a motor is not moving, and
the shaft is turned by hand or some other force, the drive will increase the motor current until the
motor returns to the commanded target position (rest position). The farther the motor is moved
from its target position, the more the torque will increase. The KP term (also called KP gain)
governs how much torque will be applied for a given amount of error (Un). In general, more load
inertia or load friction, requires more torque and therefore a higher KP gain.
Because of the topology of the control loops, the Position Control Loop output is actually a
velocity command that indirectly affects the Torque command to the motor. The Velocity command
provided by the P term is:
V = VP * Un
5.2.2 The Position Integral Term (KI) - Not Implemented
There is no KI term as it is not required because of the Velocity loop which contains an Integrator
term. Any position error will taken up and corrected for in the Velocity loop.
5.2.3 Deri Gain: The Derivative Term (KD)
A motor run with a pure PI controller would overreact to small errors, creating even larger errors
and becoming unstable. By predicting what a motor will do ahead of time, the large errors and
instability can be avoided. The derivative term determines this by analyzing the rate of change
of the position error and including that in the torque calculation. For example, if the motor has a
position error, but the rate of change of the error is decreasing, torque is lowered. The formula
used here is:
V = KP * Un + KD * (Un – (Un-1))
















































