14
08
Approximate solutions to higher
order equations
(bisection method)
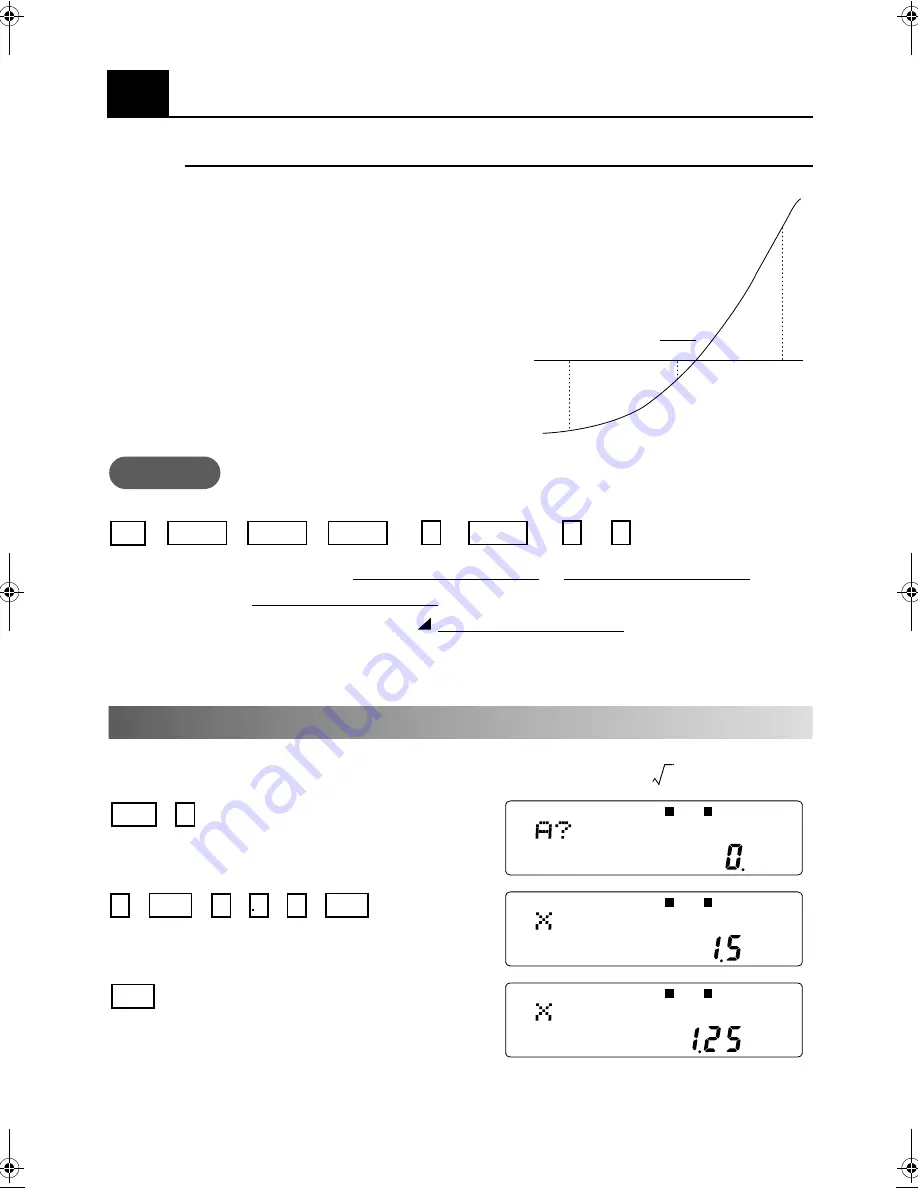
Let
be a function continuous on the interval
, with
and
having opposite signs, so
that there must be at least one in
with
. If we divide the interval into two,
must belong to one of the intervals. Thus by
comparing the signs of
, and
we can half the interval in which we search.
Repeating this procedure will yield an approximate
solution of arbitrary accuracy.
Program
Lbl 1:?→ A:?→ B:
(
)(
)≧0
⇒ Goto 1:
(
)>0⇒ Goto 2:B → C:A → B:C →
A:Lbl 2:
(A + B)÷2→ X:X
→ Y:Y >0⇒ Goto
3:X → B:Goto 2:Lbl 3:X → A:Goto 2 <
126 STEP
>
Execution Example:
Find solutions to the equation
. (Solutions are
and )
a
b
a+b
2
f x
( )
a b
[ , ]
f a
( )
f b
( )
c
a b
[ , ]
f c
( )
0
=
c
f a
( )
f
a
b
+
2
-------------
,
f b
( )
ON
MODE
MODE
MODE
1
PRGM
MODE
1
COMP
1
P1
A
3
-2 A
2
-2 A +4
B
3
-2 B
2
-2 B +4
A
3
-2 A
2
-2 A +4
X
3
-2 X
2
-2 X +4
x
3
2
x
2
–
2
x
–
4
+
0
=
2
±
2
Prog
1
S A
D R
P1
P1 P2 P3 P4
G
1
EXE
1
5
EXE
Disp
S A
D R
P1
P1 P2 P3 P4
G
EXE
Disp
S A
D R
P1
P1 P2 P3 P4
G
関数電卓事例集
.book
1
4
ページ
2002年9月2日 月曜日 午後6時51分
Содержание 3950P
Страница 1: ......
Страница 46: ...MEMO MEMO MEMO MEMO...
Страница 47: ...Authors Dr Yuichi Takeda Research and Development Initiative Chuo University...
Страница 48: ......






























