S
IMPLE
F
REQUENCY
SWEEP
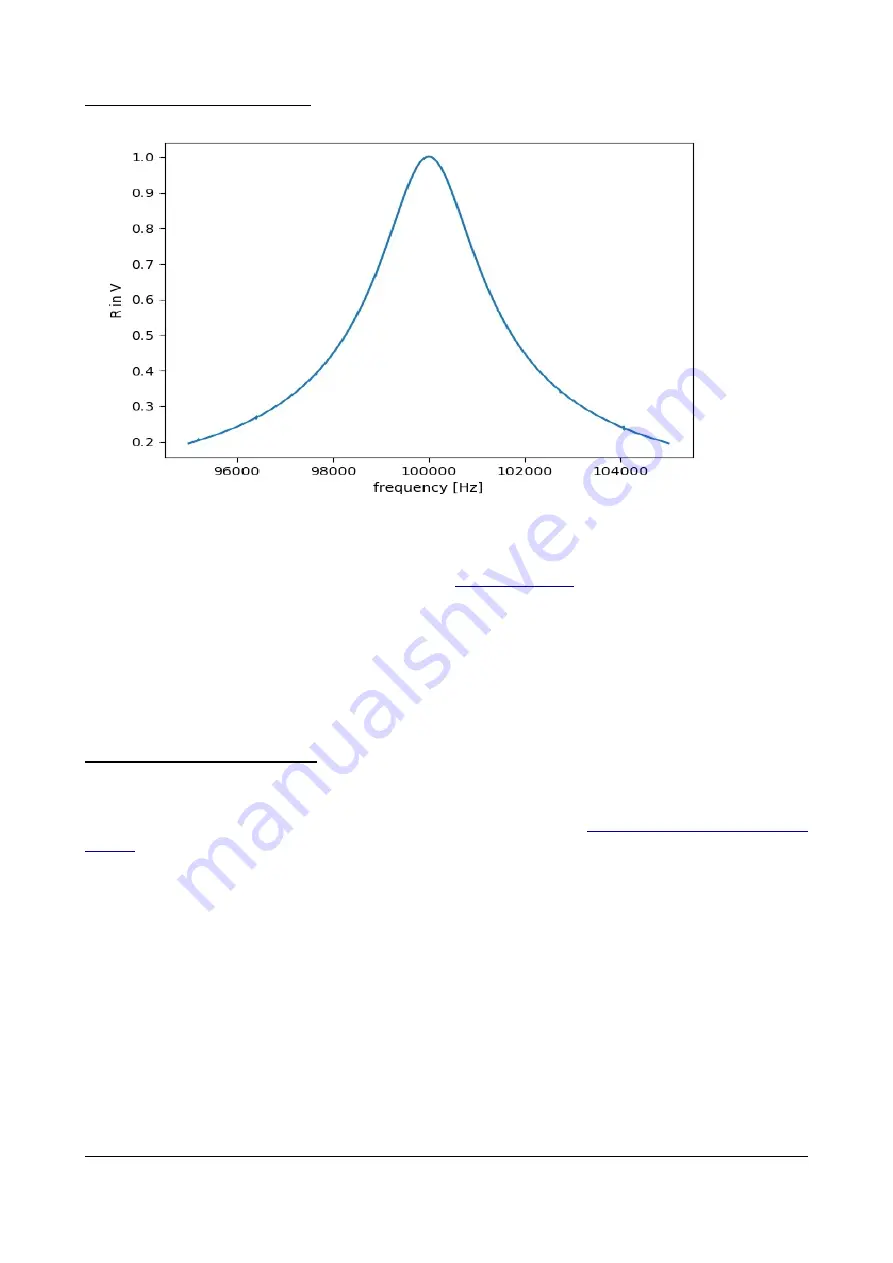
One nice way to understand the effect of the
onto the bandwidth of lockin
detection is to provide an ideal sine wave with one well defined frequency from an external
function generator to the lockin's input. Then, sweep the centre frequency of the lockin. If the
centre frequency equals the external sine wave frequency, it detects exactly its amplitude. If the
center frequency is 1/t off the external sine wave, it detects 0.7 times the amplitude. It practically
is folding the lockin's detection bandwidth with the delta-spike like input and thus visualizing the
detection bandwidth itself.
E
XAMPLE
F
OURIER
A
NALYSE
Lockin amplifiers can be used to transform time dependent signals into the frequency space and
thus detect periodicities in these signals. This method is also known as Fourier analysis or
spectrum analyzer function. One easy to understand example is the
Square signals can be mathematically generated from a series of an infinite amount of
polynomials containing the odd orders only. Thus, a f0 = 10 kHz square wave analyzed with a
spectrum analyser shows all frequency components (n+1)*f0 with n being a whole number n =
0 ... ∞.
In analogy, the frequency spectrum taken with a lockin amplifier shows the result in Fig. 50:
Manual Anfatec PCI-Lockin Amplifier AMU2.4 – Rev. 1.10 dated 30/09/20
Page 51 (70)
Figure 39: Detected amplitude of a sine-wave input signal with 1 V amplitude and 100 kHz frequency from an
function generator. The time constant is set to 1 ms, so that the detection bandwidth is 1 kHz.
















































