Calculating moment of inertia
105
1
2
3
4
Apx
6
7
8
9
10
11
付
A
ppe
ndi
x
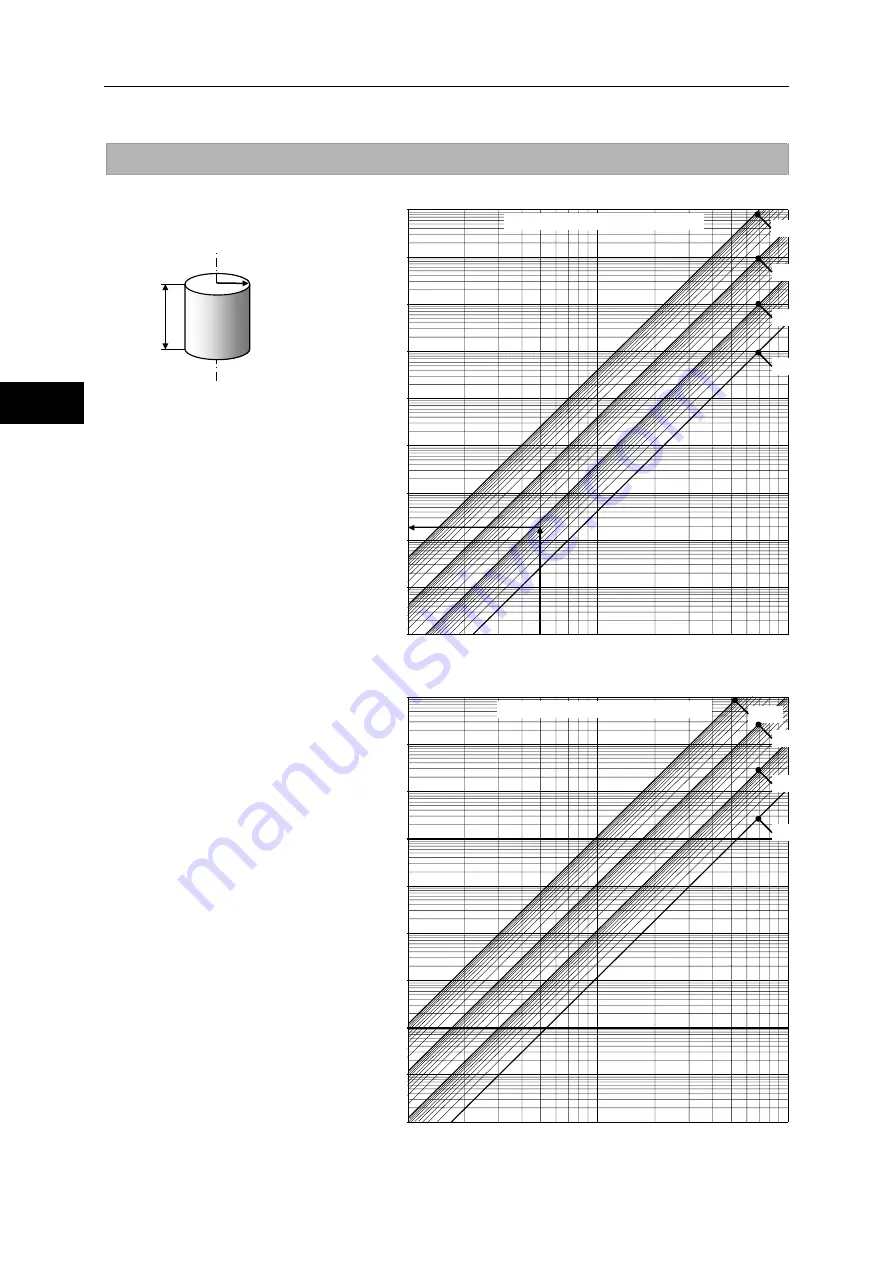
Moment of inertia of a cylinder
The inertia moment of a cylinder
may be obtained from the graphs to
the right.
Apply the top graph to aluminum
materials (specific gravity: 2.7) and
bottom graph to steel materials
(specific gravity: 7.85).
(Example)
Material: Aluminum
Outer diameter: 100mm
Length: 7mm
Shape: Column
Since the outer diameter is 100mm,
the radius is 50mm. Therefore, the
above graph gives the inertia
moment as follows:
Approx. 1.9
x 10
-4
kg
・
m
2
(Calculated value:
0.000186
kg
・
m
2
)
Radius
Length
1000
100
10
1
0.1
0.01
0.001
10
-4
10
-5
10
-6
10
100
1000
20
30
50
70
200 300
500 700
Inertia moment (specific gravity: 2.7)
Inertia moment (kgm
2
)
Radius R (mm)
Length (mm)
1000
100
10
1
1000
100
10
1
0.1
0.01
0.001
10
-4
10
-5
10
-6
10
100
1000
20
30
50
70
200 300
500 700
Inertia moment (specific gravity: 7.85)
Inertia moment (kgm
2
)
Radius R (mm)
Length (mm)
1000
100
10
1





































