Harmonic Drive RSF-11B, Manual

Page: 26 / 32

Appendix 2 Calculations of moment of inertia
- Appendix 2-1 -
Appendix 2 Calculations of moment of inertia
1. Calculation formulas for mass and moment of inertia
(1) When center of revolution and line of center of gravity match
Calculation formulas for mass and moment of inertia are shown below.
m: Mass (kg)
Ix, Iy, Iz: moment of inertia (kgm
2
) making Axes x, y and z as centers of revolution
G: Distance from edge surface of center of gravity
ρ : Specific gravity
Units - Length: m, mass: kg, moment of inertia: kgm
2
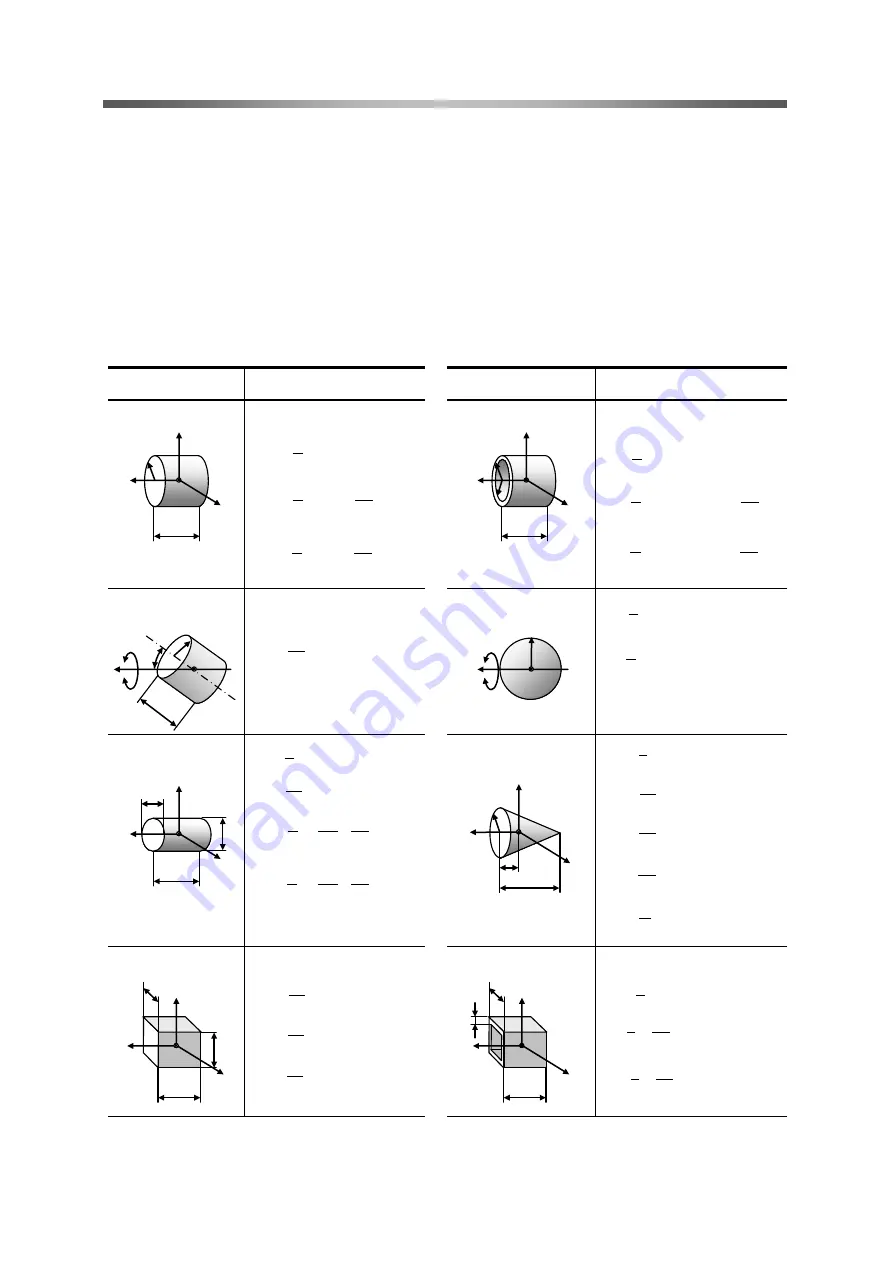
Shape of object
Mass, inertia,
position of center of gravity
Shape of object
Mass, inertia,
position of center of gravity
Circular cylinder Round pipe
Tilted circular cylinder Sphere
Elliptic circular cylinder Cone
Prism Regular square pipe
R
L
z
x
y
ρ L R m
2
π =
2
R m
2
1
Ix
=








+ =
3
L
R m
4
1
Iy
2
2








+ =
3
L
R m
4
1
Iz
2
2
R
1
L
R
2
z
x
y
R
1
: Outside diameter
R
2
: Inside diameter
( )
ρ
L R R m
2
2
2
1
− =
π
( )








+ + =
3
L
R R m
4
1
Iy
2
2
2
2
1
( )
2
2
2
1
R R m
2
1
Ix + =
( )








+ + =
3
L
R R m
4
1
Iz
2
2
2
2
1
B
L
z
x
y
C
ρ L BC m
π
4
1
=
( )
2 2
C B m
16
1
Ix
+ =








+ =
3
L
4
C
m
4
1
Iy
2 2








+ =
3
L
4
B
m
4
1
Iz
2 2
R
L
z
x
y
G
ρ
1
L R
3
m
2
π
=
2
R m
10
3
Ix
=
( )
2 2
L 4R m
80
3
Iy
+ =
( )
2 2
L 4R m
80
3
Iz + =
4
L
G =
z
x
y
C
B
A
ρ A
BC m
=
(
)
2 2
C B m
12
1
Ix + =
( )
2 2
A C m
12
1
Iy
+ =
(
)
2 2
B A m
12
1
Iz + =
D B
A
z
x
y
( )
ρ D - B 4AD = m
( )
{ }
2
2
D D - B m
3
1
Ix + =
( )






+ + =
2
2
2
D D - B
A
m
6
1
Iy
2
( )






+ + =
2
2
2
D D - B
2
A
m
6
1
Iz
ρ L R m
2
π =
( ) { }
θ θ
2 2 2 2
sin L cos 1 3R
m
12
1
I
+ + ×
=
θ
R
L
θ
R
ρ
3
R
3
4
m
π
=
2
R m
5
2
I
=