- 9 -
Introduction to
NTC
and
S
ensitivity
T
he
NTC
sensitivity about
temperature changes also represent
s
resistance
’
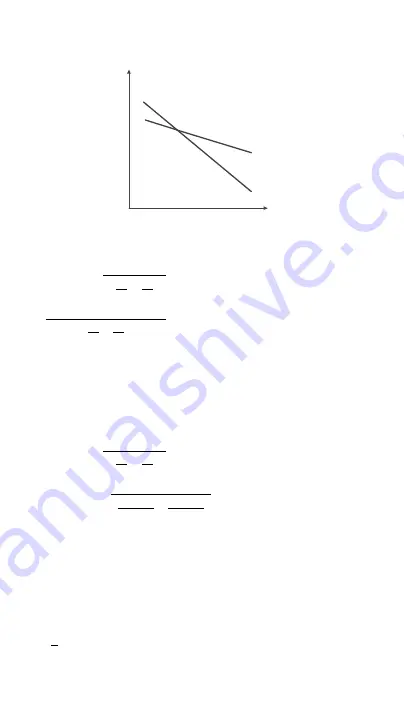
s rate of changes, which can
be seen from the slope of the line in the chart below. The greater the slope the higher the sensitivity;
therefore, the sensitivity of line A would be
higher than line B as a result of a greater slope.
Temperature
(T)
Resistance
(R
)
A
High Sensitivity
B
Low Sensitivity
The result of sensitivity formula is determined by the rate of change on resistance
between temperature1
and temperature2. The formula is shown below.
Sensitivity =
ln
𝑅𝑅
1
−
ln
𝑅𝑅
2
1
𝑇𝑇
1
−
1
𝑇𝑇
2
=
2.3026(log
𝑅𝑅
1
−
log
𝑅𝑅
2
)
1
𝑇𝑇
1
−
1
𝑇𝑇
2
Sensitivity (
𝐾𝐾
)
𝑅𝑅
1
=
𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅
(
Ω
)
𝑅𝑅𝑅𝑅
𝑅𝑅𝑎𝑎𝑅𝑅𝑎𝑎𝑎𝑎𝑎𝑎𝑅𝑅𝑅𝑅
𝑅𝑅𝑅𝑅𝑡𝑡𝑡𝑡𝑅𝑅𝑡𝑡𝑅𝑅𝑅𝑅𝑎𝑎𝑡𝑡𝑅𝑅
𝑇𝑇
1
(
𝐾𝐾
)
𝑅𝑅
2
=
𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅
(
Ω
)
𝑅𝑅𝑅𝑅
𝑅𝑅𝑎𝑎𝑅𝑅𝑎𝑎𝑎𝑎𝑎𝑎𝑅𝑅𝑅𝑅
𝑅𝑅𝑅𝑅𝑡𝑡𝑡𝑡𝑅𝑅𝑡𝑡𝑅𝑅𝑅𝑅𝑎𝑎𝑡𝑡𝑅𝑅
𝑇𝑇
2
(
𝐾𝐾
)
For example,
PT-
42H 10K B25 B85 3435K
means the resistance
value
of the sensor is
10K
Ω
at 25°C
,
while
B25 B85 3435K
indicates
that the sensitivity value is
3435K
at a temperature between 25°C~85°C.
Sensitivity =
ln
𝑅𝑅
1
−
ln
𝑅𝑅
2
1
𝑇𝑇
1
−
1
𝑇𝑇
2
=
ln 1451
−
ln 10,000
1
358.15
−
1
298.15
= 3435.42
≅
3435
𝑅𝑅
1
=
𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅
𝑅𝑅𝑅𝑅
25°C = 10K
Ω
𝑅𝑅
2
=
𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅𝑅
𝑅𝑅𝑅𝑅
85°C =
1451Ω
𝑇𝑇
1
= 25 + 273.15 = 298.15K
𝑇𝑇
2
= 85 + 273.15 = 358.15K
K = °C + 273.15
K =
5
9
× (°F
−
32) + 273.15










































