CS5530
DS742F3
27
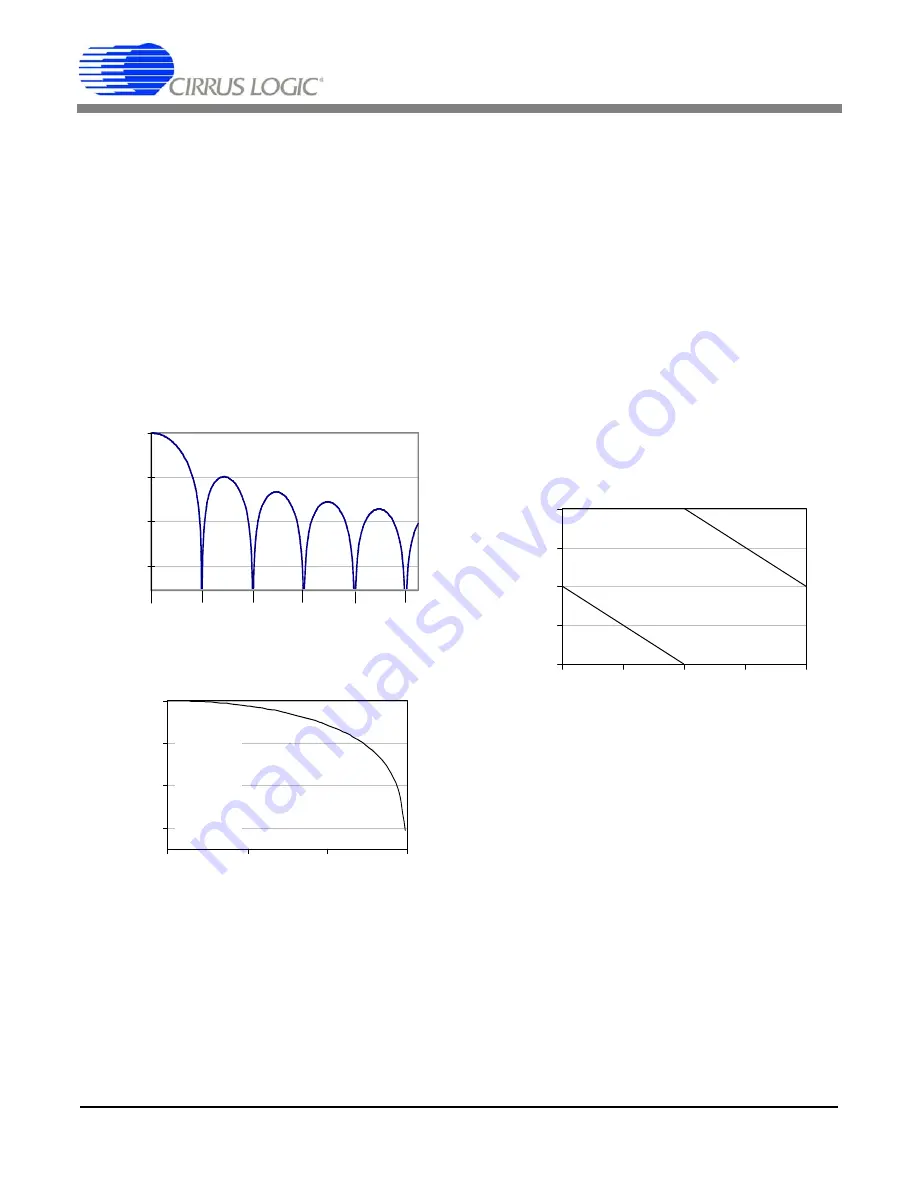
2.8 Digital Filter
The CS5530 has a linear phase digital filter which
is programmed to achieve a range of output word
rates (OWRs) as stated in the
Configuration Regis-
ter Description
section. The ADC uses a Sinc
5
dig-
ital filter to output word rates at 3200 Sps and 3840
Sps (MCLK = 4.9152 MHz). Other output word
rates are achieved by using the Sinc
5
filter followed
by a Sinc
3
filter with a programmable decimation
rate.Figure 13 shows the magnitude response of the
60 Sps filter, while Figures 14 and 15 show the
magnitude and phase response of the filter at 120
Sps. The Sinc
3
is active for all output word rates
except for the 3200 Sps and 3840 Sps (MCLK =
4.9152 MHz) rate. The Z-transforms of the two fil-
ters are shown in Figure 16. For the Sinc
3
filter,
“D” is the programmable decimation ratio, which is
equal to 3840/OWR when FRS = 0 and 3200/OWR
when FRS = 1.
The converter’s digital filters scale with MCLK.
For example, with an output word rate of 120 Sps,
the filter’s corner frequency is at 31 Hz. If MCLK
is increased to 5.0 MHz, the OWR increases by
1.0175 percent and the filter’s corner frequency
moves to 31.54 Hz. Note that the converter is not
specified to run at MCLK clock frequencies greater
than 5 MHz.
Figure 13. Digital Filter Response (Word Rate = 60 Sps)
-120
-80
-40
0
Gain
(dB)
0
60
120
180
240
300
Frequency (Hz)
FRS = 0
-120
-80
-40
0
0
40
80
120
Frequency (Hz)
G
a
in
(
d
B
)
Flatness
Frequency
dB
2
-0.01
4
-0.05
6
-0.11
8
-0.19
10
-0.30
12
-0.43
14
-0.59
16
-0.77
19
-1.09
32
-3.13
Figure 14. 120 Sps Filter Magnitude Plot to 120 Hz
-180
-90
0
90
180
0
30
60
90
120
Frequency (Hz)
P
h
ase (
D
eg
rees)
Figure 15. 120 Sps Filter Phase Plot to 120 Hz
Note:
See the text regarding the Sinc
3
filter’s
decimation ratio “D”.
Sinc
5
1
z
80
–
–
(
)
5
1
z
16
–
–
(
)
5
--------------------------
1
z
16
–
–
(
)
3
1
z
4
–
–
(
)
3
--------------------------
1
z
4
–
–
(
)
2
1
z
2
–
–
(
)
2
-----------------------
1
z
2
–
–
(
)
3
1
z
1
–
–
(
)
3
-----------------------
×
×
×
=
Sinc
3
1
z
D
–
–
(
)
3
1
z
1
–
–
(
)
3
-------------------------
=
Figure 16. Z-Transforms of Digital Filters











































