8
tudes of partials decrease with frequency). This
is achieved by changing the exponent γ with-
in the partial amplitude formula: A
n
=A
1
/n
γ
.
This parameter can change from 3 (very
quick decay, dull sound), through 1 (like in
the sawtooth wave) down to nearly 0 (almost
flat spectrum, very bright sound) — see fig.
5. Note that this parameter has a significant
impact on the resulting energy of the signal.
Together, the density, warp, and peak-
ing parameters control the comb-like fre-
quency response imposed on the spectrum.
The notches of the comb are produced by a
warped Sinc function in the frequency do-
main (fig. 6). Bear in mind the response re-
fers to the relative frequencies of partials, so
it scales with pitch. Depending on the den-
sity parameter, there may be zero to 256
notches, hence at minimum, the spectrum
is smooth, and at maximum, each second
partial is filtered out (only odd-numbered
partials remain), provided there is no warp.
Thus, with all other parameters set to de-
fault, turning the density knob morphs the
signal from a sawtooth to a square wave —
but quite differently than a simple crossfade!
0 0.5 1 1.5 2
Time
1
0.5
0
-0.5
-1
Amplitude
0 0.5 1 1.5 2
Time
1
0.5
0
-0.5
-1
Amplitude
5 10 15 20 25 30
Partial number
0
1
0.8
0.6
0.4
0.2
Amplitude
5 10 15 20 25 30
Partial number
0
1
0.8
0.6
0.4
0.2
Amplitude
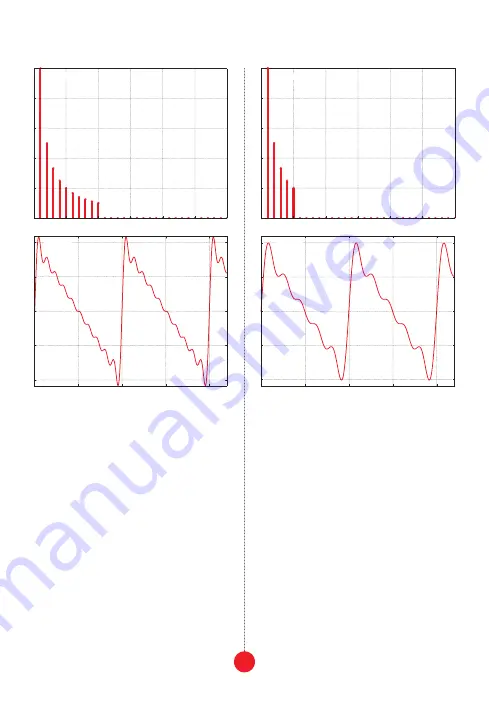
fig. 4b
sawtooth wave after limiting the spectrum
to the initial 5 partials
fig. 4a
sawtooth wave after limiting the spectrum
to the initial 10 partials