Hardware and physical integration guideline PCR Sensor A111
Page 14 of 32
© 2022 by Acconeer
– All rights reserved
2022-03-08
4.2 Radome thickness
When an EM wave travels in a dielectric material, its effective propagation speed and the wavelength
will change depending on the dielectric material:
𝑐
eff
=
𝑐
0
√𝜖
𝑟
,
𝜆
eff
=
𝜆
0
√𝜖
𝑟
where
𝜖
𝑟
is the dielectric constant of the material,
𝑐
0
is the speed of light in free space, i.e. 3×10
8
and
𝜆
0
is the free space wavelength (
𝜆
0
= 5 mm
for A111).
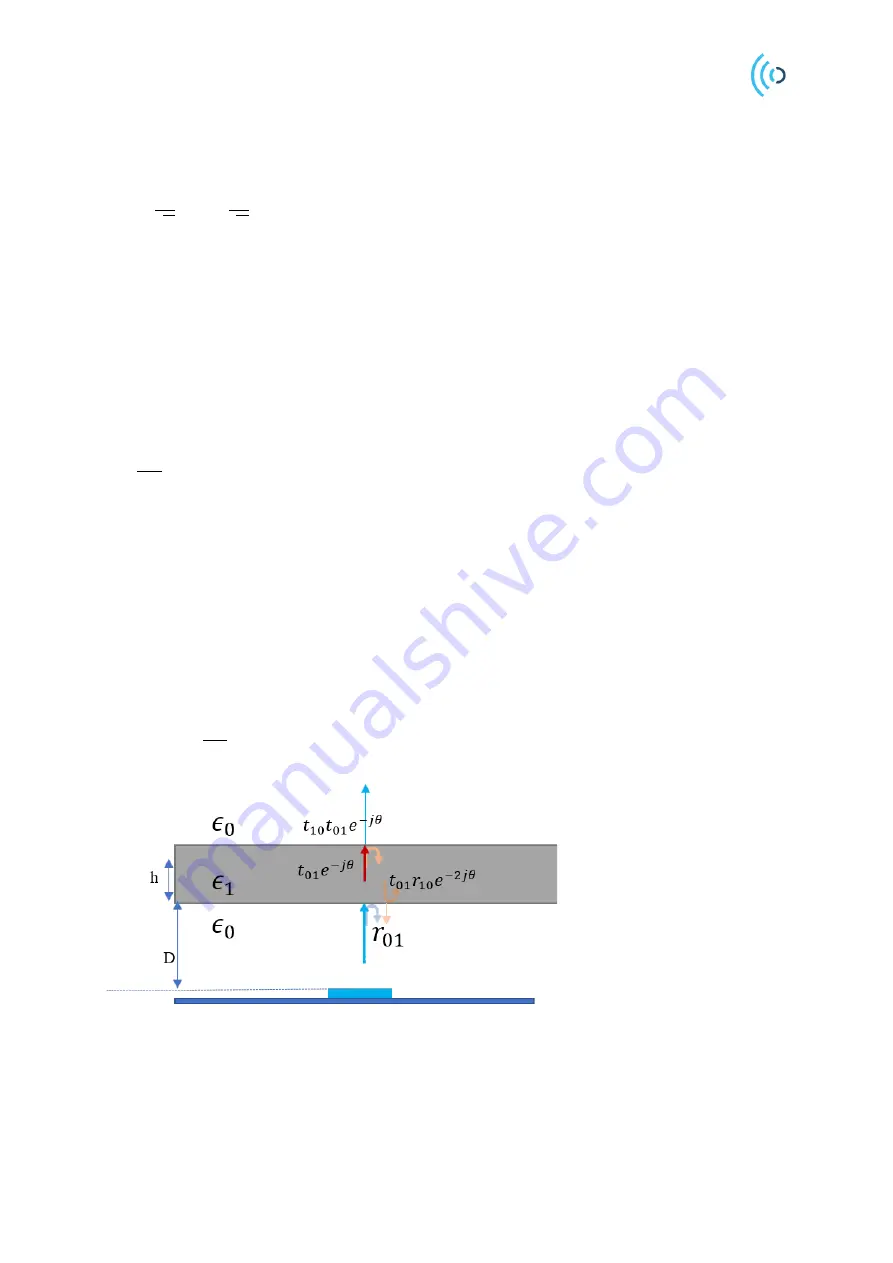
Reflections happens at the air-dielectric interfaces and the thickness of the dielectric medium determines
the phase shift of the reflected wave from dielectric-air interface. Figure 14 shows a simplified model
of the transmission and reflections of the waves between air-dielectric. Reflections from the second
bounce and above are neglected in this model. When the wave impinges the air-dielectric interface, part
of it reflects (
𝑟
01
) and part of it transmits (
𝑡
01
). The thickness of the dielectric material will cause the
wave to shift phase by:
𝜃 =
2𝜋
𝜆
eff
ℎ
where
ℎ
is the thickness of the dielectric. When the wave reaches the dielectric-air interface (
𝑡
01
𝑒
−𝑗𝜃
),
another transmission (
𝑡
10
𝑡
01
𝑒
−𝑗𝜃
) and reflections (
𝑟
10
𝑡
01
𝑒
−𝑗𝜃
) happens. Notice that the wave will have
a sign change when the reflection happens,
𝑟
10
= − 𝑟
01
. At the lower dielectric-air interface, the
amplitude of the wave is
−𝑟
01
𝑡
01
𝑒
−2𝑗𝜃
, where the wave has traveled a distance of
2ℎ
.
If we assume a half-wavelength-thick radome, the round trip of the wave inside the radome will
introduce a 360-degree phase shift. Hence, the reflected wave into the air has a
−𝑟
01
𝑡
10
𝑡
01
amplitude.
In this case, the reflected waves
, 𝑡
10
𝑡
01
≈ −𝑟
01
and 𝑟
01
will cancel out. Therefore, to minimize the
reflections, the thickness of a single layer radome should be half-a-wavelength or a multiple of it.
ℎ
optimum
= 𝑛
𝜆
eff
2
, 𝑛 = 1,2,3, …
Figure 14. Incident wave impinging the radome at the normal incident angle. Transmission and reflection of the wave
at the interfaces of two mediums.
As an example, a plastic sheet made of ABS with different thicknesses was selected for the test
measurement. If we assume dielectric constant of ABS to be 2.6 (the dielectric constant can vary
depending on the vendor), the thickness of the half-a-wavelength-thick radome is calculated to be















































