C
OPYING PERMITTED PROVIDED
TI
COPYRIGHT NOTICE IS INCLUDED
© T
EXAS
I
NSTRUMENTS
I
NCORPORATED
G
ETTING
S
TARTED WITH
CBR
25
Activity 4—Bouncing ball
notes for teachers
Concepts
Function explored: parabolic.
Real-world concepts such as free-falling and bouncing
objects, gravity, and constant acceleration are
examples of parabolic functions. This activity
investigates the values of height, time, and the
coefficient
A
in the quadratic equation,
Y = A(X – H)
2
+ K
, which describes the behavior of a
bouncing ball.
Materials
Ÿ
calculator
Ÿ
CBR
Ÿ
calculator-to-CBR cable
Ÿ
large (9-inch) playground ball
Ÿ
TI ViewScreen (optional)
Hints
This activity is best performed with two students, one
to hold the ball and the other to push
¤
.
See pages 6–12 for hints on effective data collection.
The plot should look like a bouncing ball. If it does
not, repeat the sample, ensuring that the
CBR
is aimed
squarely at the ball. A large ball is recommended.
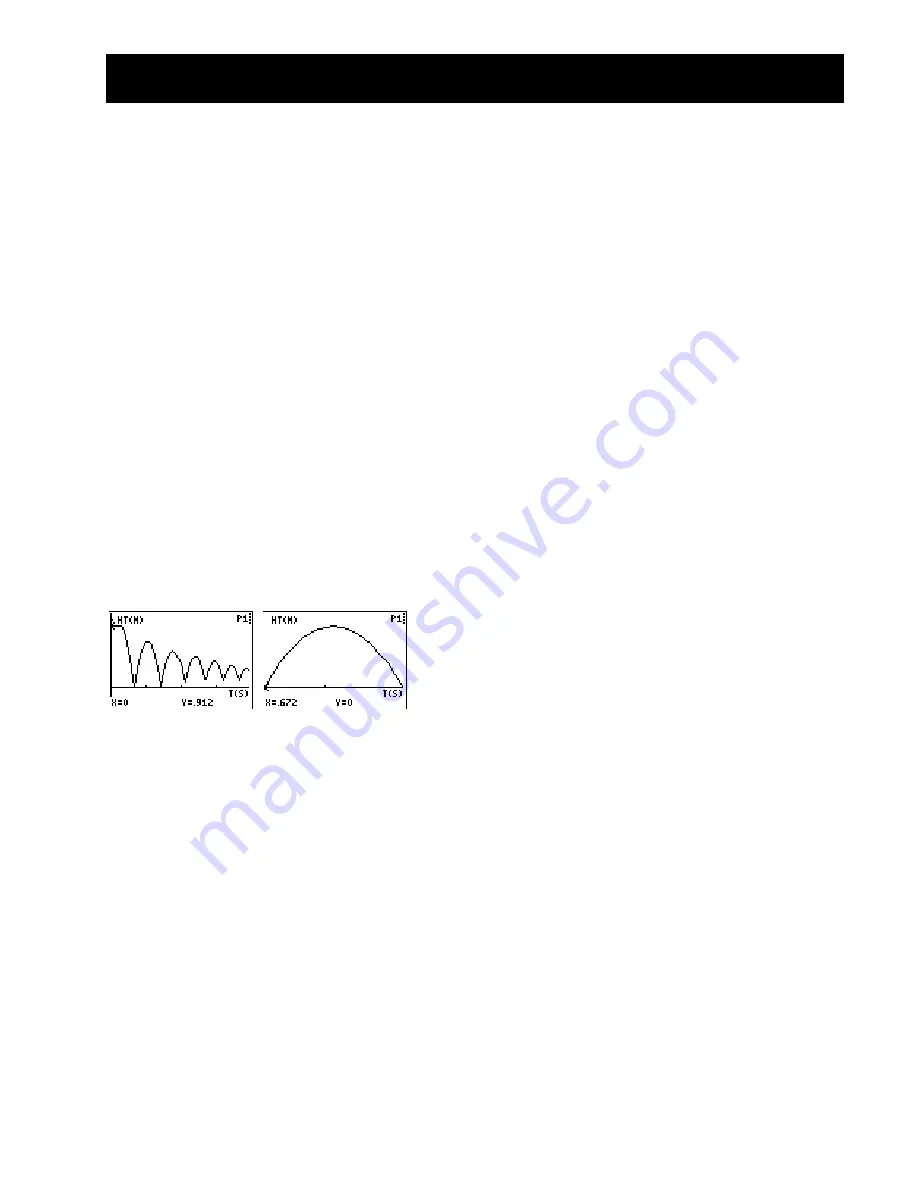
Typical plots
Explorations
After an object is released, it is acted upon only by
gravity (neglecting air resistance).
So
A
depends on the
acceleration due to gravity,
N
9.8 meters
à
second
2
(
N
32 feet
à
second
2
).
The negative sign indicates that
the acceleration is downward.
The value for
A
is approximately one-half the
acceleration due to gravity, or
N
4.9 meters
à
second
2
(
N
16 feet
à
second
2
).
Typical answers
1. time (from start of sample); seconds; height
à
distance of the ball above the floor; meters or feet
2. initial height of the ball above the floor (the peaks
represent the maximum height of each bounce);
the floor is represented by y = 0.
3. The Distance-Time plot for this activity does not
represent the distance from the
CBR
to the ball.
BALL BOUNCE
flips the distance data so the plot
better matches students’ perceptions of the ball’s
behavior. y = 0 on the plot is actually the point at
which the ball is farthest from the
CBR
, when the
ball hits the floor.
4. Students should realize that the x-axis represents
time, not horizontal distance.
7. The graph for
A
= 1 is both inverted and broader
than the plot.
8.
A
<
L
1
9. parabola concave up; concave down; linear
12. same; mathematically, the coefficient
A
represents
the extent of curvature of the parabola; physically,
A
depends upon the acceleration due to gravity,
which remains constant through all the bounces.
Advanced explorations
The rebound height of the ball (maximum height for a
given bounce) is approximated by:
y
=
hp
x
, where
0
y
is the rebound height
0
h
is the height from which the ball is released
0
p
is a constant that depends on physical
characteristics of the ball and the floor surface
0
x
is the bounce number
For a given ball and initial height, the rebound height
decreases exponentially for each successive bounce.
When
x
= 0,
y
=
h
, so the y-intercept represents the
initial release height.
Ambitious students can find the coefficients in this
equation using the collected data. Repeat the activity
for different initial heights or with a different ball or
floor surface.
After manually fitting the curve, students can use
regression analysis to find the function that best
models the data. Select a single bounce using
PLOT
TOOLS
,
SELECT DOMAIN
. Then
QUIT
from the
MAIN MENU
.
Follow the calculator operating procedures to perform
a quadratic regression on lists
L1
and
L2
.
Extensions
Integrate under Velocity-Time plot, giving the
displacement (net distance traveled) for any chosen
time interval. Note the displacement is zero for any full
bounce (ball starts and finishes on floor).
















































