2
G
(
s
)
'
s
s %
(1/
RC
) ×
1
[
s %
(1/
RC
)]
n
(
n 6 4
)
causes an undershoot whose peak amplitude is
roughly determined from:
undershoot amplitude
=
differentiated pulse amplitude
differentiation time
preamplifier pulse decay time
For a 1-µs differentiation time constant and a 50-µs
preamplifier pulse decay time, the maximum
undershoot is 2% and this decays with a 50-µs time
constant. Under overload conditions, this
undershoot is often sufficiently large to saturate the
amplifier during a considerable portion of the
undershoot, causing excessive dead time. This
effect can be reduced by increasing the
preamplifier pulse decay time (which generally
reduces the counting rate capabilities of the
preamplifier) or compensating for the undershoot
by using pole-zero cancellation.
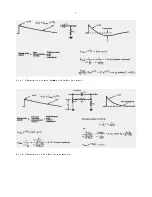
Pole-zero cancellation is accomplished by the
network shown in Fig. 1.2. The pole [s + (1/
T
o
)] due
to the preamplifier pulse decay time is canceled by
the zero of the network [s + (K/R
2
C
1
)]. In effect, the
dc path across the differentiation capacitor adds an
attenuated replica of the preamplifier pulse to just
cancel the negative undershoot of the
differentiating network.
Total preamplifier-amplifier pole-zero cancellation
requires that the preamplifier output pulse decay
time be a single exponential decay and matched to
the pole-zero-cancellation network. The variable
pole-zero-cancellation network allows accurate
cancellation for all preamplifiers having 40-µs or
greater decay times. Improper matching of the
pole-zero-cancellation network will degrade the
overload performance and cause excessive pileup
distortion at medium counting rates. Improper
matching causes either an under-compensation
(undershoot is not eliminated) or an over-
compensation(outputafterthemainpulsedoesnot
return to the baseline and decays to the baseline
with the preamplifier time constant). The pole-zero
adjust is accessible from the front panel of the
572A and can easily be adjusted by observing the
baselinewithanoscilloscopewithamonoenergetic
source orpulserhavingthesamedecaytime as the
preamplifier under overload conditions. The
adjustment should be made so that the pulse
returns to the baseline in the minimum time with no
undershoot.
1.3. ACTIVE FILTER
When only FET gate current and drain thermal
noise are considered, the best signal-to-noise ratio
occurs when the two noise contributions are equal
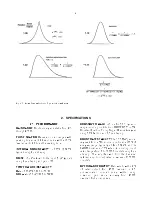
for a given input pulse shape. The Gaussian pulse
shape (Fig. 1.3) for this condition requires an
amplifier with a single RC differentiate and n equal
RC integrates where n approaches infinity.
The Laplace transform of this transfer function is:
where the first factor is the single differentiate and
the second factor is the n integrates. The 572A
active filter approximates this transfer function.
Figure 1.3 illustrates the results of pulse shaping in
an amplifier. Of the four pulse shapes shown the
cusp would produce minimum noise but is
impractical to achieve with normal electronic
circuitry and would be difficult to measure with an
ADC. The true Gaussian shape deteriorates the
signal-to-noise ratio by only about 12% from that of
the cusp and produces a signal that is easy to
measure, but requires many sections of integration
(n
6 4
). With two sections of integration the
waveform identified as a Gaussian approximation
canbeobtained,andthisdeterioratesthesignal-to-
noise ratio by about 22%. The ORTEC active filter
network in the 572A Amplifier provides the fourth
waveform in Fig. 1.3; this waveform has
characteristics superior to the Gaussian
approximation, yet obtains them with four complex
poles. By this method the output pulse shape has
a good signal-to-noise ratio, is easy to measure,
and yet requires only a practical amount of
electronic circuitry to achieve the desired results.
Summary of Contents for 572A
Page 6: ...vi...