where Kt and J are as defined previously. For example, a current amplifier with Ka = 2 A/V with the
motor described by the previous example will have the transfer function:
P/V
=
1000/s2 [rad/V]
If the motor is a DC brushless motor, it is driven by an amplifier that performs the commutation. The
combined transfer function of motor amplifier combination is the same as that of a similar brush
motor, as described by the previous equations.
Velocity Loop
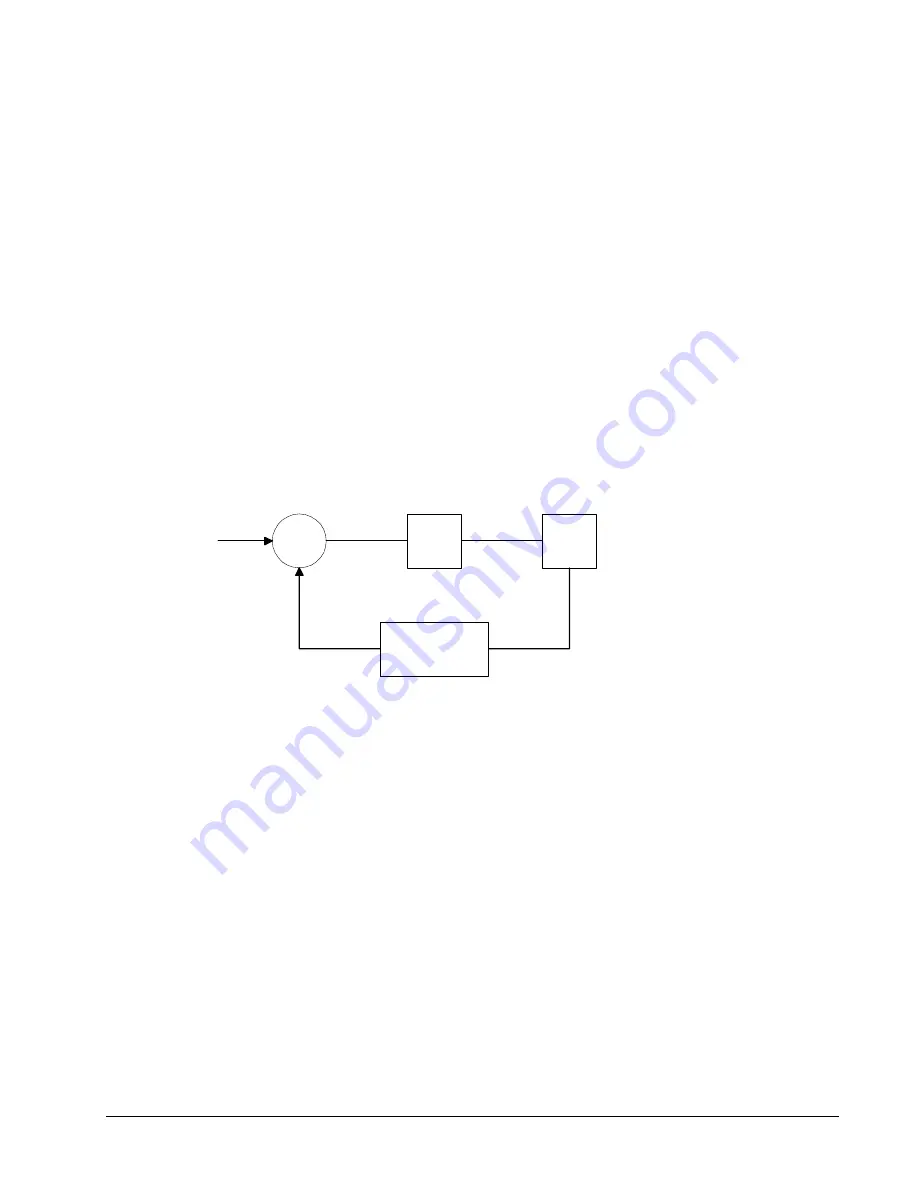
The motor driver system may include a velocity loop where the motor velocity is sensed by a
tachometer and is fed back to the amplifier. Such a system is illustrated in Fig. 10.5. Note that the
transfer function between the input voltage V and the velocity
ω
is:
ω
/V = [Ka Kt/Js]/[1+Ka Kt Kg/Js] = 1/[Kg(sT1+1)]
where the velocity time constant, T1, equals
T1 = J/Ka Kt Kg
This leads to the transfer function
P/V
=
1/[Kg s(sT1+1)]
Σ
K
a
Kt/Js
K
g
V
Figure 10.5 - Elements of velocity loops
The resulting functions derived above are illustrated by the block diagram of Fig. 10.6.
142
i
Chapter 10 Theory of Operation
DMC-14x5/6
Artisan Technology Group - Quality Instrumentation ... Guaranteed | (888) 88-SOURCE | www.artisantg.com






























