35
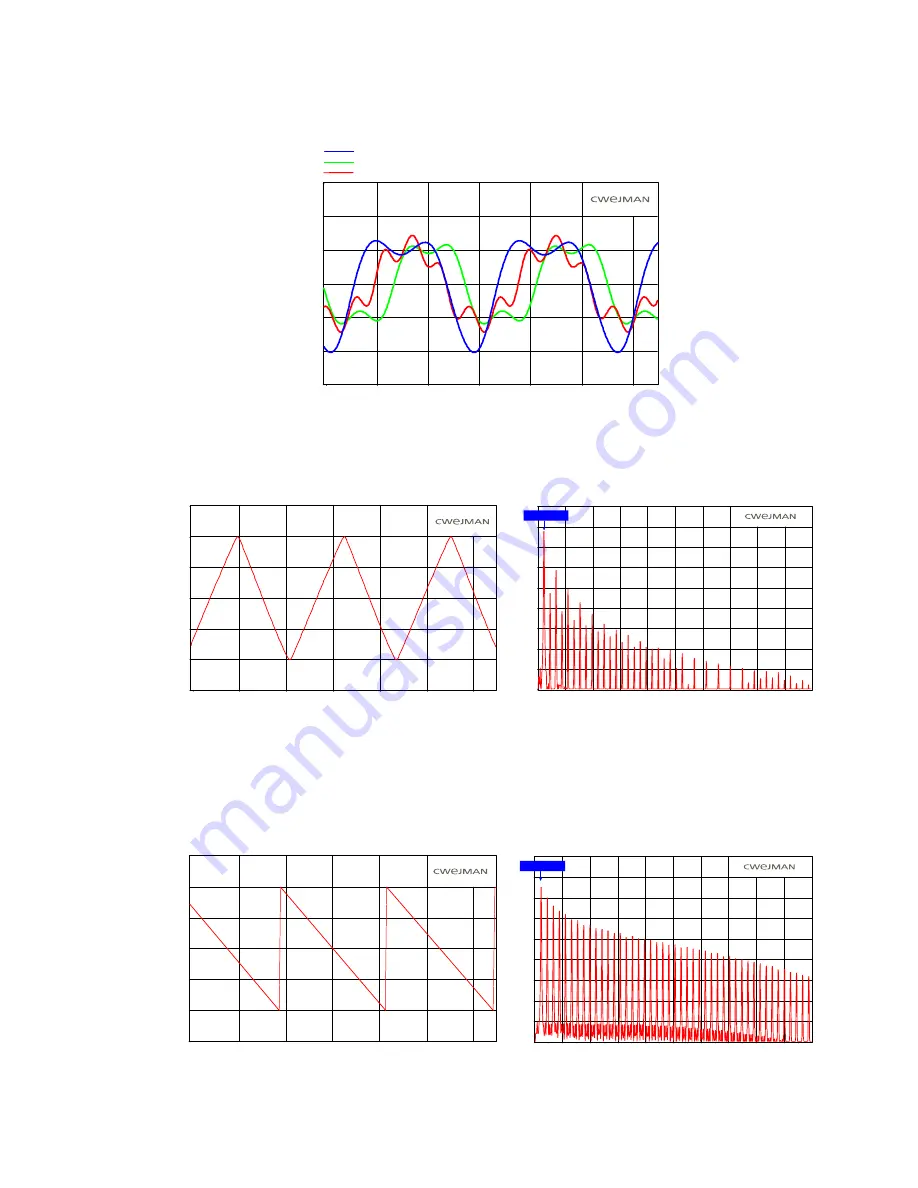
In other words the sine wave has its own character, it sounds nearly clean but it can change its timbre by,
e.g.a filter sweep (dynamic) or by a filter with a peak frequency that corresponds with the harmonic
overtones of the signal (static). The illustration below shows the result of modifying the signal with
the Lowpass Filter and Q-peak = 7.
FILTERED SINUS WAVEFORM BY LOW-PASS FILTER
O
U
TP
U
T
(V
ol
ts
)
5.0
2.5
0.0
-2.5
-5.0
-7.5
3.00
4.00
5.00
6.00
7.00
8.00
Time (milliseconds)
7.5
PEAK @ SECOND HARMONIC TONE
PEAK @ THIRD HARMONIC TONE
PEAK @ FIFTH HARMONIC TONE
Triangle Waveform
This waveform has a higher content of overtones than the sine wave and consequently sounds
different. The odd overtones are most prominent. The amplitude of the overtones is higher than
those in the sine wave but also diminish more rapidly.
OSCILLATOR OUTPUT, TRIANGLE, A440
O
U
TP
U
T
(V
ol
ts
)
5.0
2.5
0.0
-2.5
-5.0
-7.5
3.00
4.00
5.00
6.00
7.00
8.00
Time (milliseconds)
7.5
dB
V
rm
s
0.0
-10.0
-20.0
-30.0
-40.0
-50.0
-60.0
-70.0
-80.0
-90.0
1.0k
3.0k
5.0k
7.0k
9.0k
11.0k 13.0k 15.0k 17.0k 19.0k
Frequency (Hz)
440.00 Hz
Sawtooth Waveform
The sawtooth wave is the classic waveform and perhaps the most used in the creation of many
characteristic bass and brass synthesizer sounds. This is due to the fact that the sawtooth wave
contains both even overtones (2, 4, 6,…) and odd overtones (3, 5, 7,…) that have high amplitudes
even for overtones of higher order. By dynamic and/or static filtering the character of the sound can
be altered in many ways. See the illustration below.
O
U
TP
U
T
(V
ol
ts
)
5.0
2.5
0.0
-2.5
-5.0
-7.5
3.00
4.00
5.00
6.00
7.00
8.00
Time (milliseconds)
7.5
dB
V
rm
s
0.0
-10.0
-20.0
-30.0
-40.0
-50.0
-60.0
-70.0
-80.0
-90.0
1.0k
3.0k
5.0k
7.0k
9.0k
11.0k 13.0k 15.0k 17.0k 19.0k
Frequency (Hz)
440.00 Hz
OSCILLATOR OUTPUT, SAW TOOTH, A440










































