Yamaha P-2200/2201, Руководство по эксплуатации продукта

Страница: 54 / 59

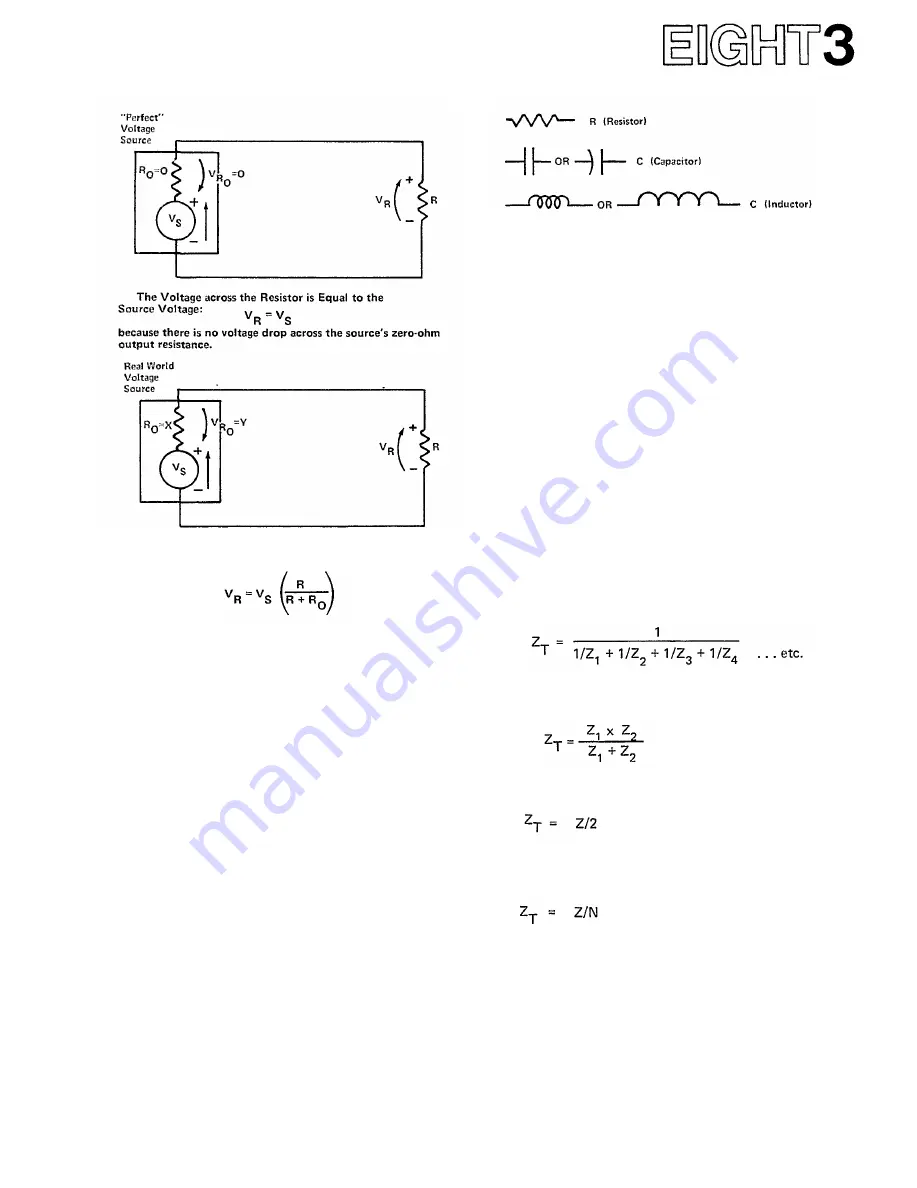
The Voltage across the Resistor is Less Than the Source
Voltage due to the voltage drop across the output resistor R
O
:
An "Impedance" is some combination (one, two, three or
more components connected together in a circuit) of Resistors,
Capacitors and Inductors.
Fig. 80 - Elements of an Impedance.
simple ohmic value, so long as only one frequency is
used. However, single frequencies are not representative
of audio sources (except for test tones), so this is a good
place to make a simplifying assumption: the impedances
that we work with in audio can be treated like pure
resistances over the entire audio frequency range. This is
a good assumption, in most cases, and we have used it
throughout this manual. When the occasional exception
shows up, we have treated it separately. If we had to
deal with an actual impedance value (made up of a pure
resistance and a reactance), most of the formulas we use
would be the same, but we would have to deal with
complex numbers (with a real and imaginary part)
instead of simple ohmic values.
SERIES AND PARALLEL
IMPEDANCE CONNECTIONS
Figure 81 diagrams the differences between series and
parallel connected impedances. The total impedance, Z
T,
of a set of series connected impedances is simply their
algebraic sum. The total impedance of a set of parallel
connected impedances is given by the following formula:
NOTE: X is the output resistance (or impedance) of the
source. Y is the voltage drop across the output resistance which
varies depending on other circuit parameters.
Fig. 79 - Voltage Sources.
IMPEDANCE
A "pure" resistance would maintain the same value,
in ohms, even if the voltage or current source changed
from a DC source to an AC source at any frequency. On
the other hand, an impedance is made of a pure resistance
connected to a reactance (a capacitor, an inductor, or
some combination of the two). The value, in ohms, of
the magnititude of an impedance changes with frequency,
making it more challenging to manipulate mathematically.
"Pure" circuit components (a perfect voltage source,
perfect current source or pure resistance) do not exist
in the real world, and audio circuits seldom deal with DC
sources, except for occasional batteries and DC power
supplies. However, the P-2200 can be considered to be
a perfect voltage source because it behaves in this
manner within its specified operating limits. Similarly,
a source such as a mixer that is feeding the P-2200 can
be considered to be a perfect voltage source in series
with a pure resistance, the resistance being equal to the
mixer's output impedance. Even a speaker impedance
can be considered to be a pure resistance in some cases,
though in other cases the variation of a speaker's
impedance with frequency must be considered. The
behavior of audio circuits is more easily explained by
making these and other, similar assumptions.
To illustrate a typical assumption, consider that any
impedance can be treated as a pure resistance having a
When there are only two impedances connected in
parallel, the formula can be simplified to:
If the two impedances are the same ohmic value, the
formula further simplifies to:
This final simplified formula is valid for any number
(N) of parallel impedances provided that their ohmic
values are a/I the same:
To calculate the power dissipated in any of the
impedances (any branch) of the circuits of Figure 81,
simply find the voltage across that impedance or the
current through the impedance, (using the voltage
and current division rules that follow). Alternately, find
both the voltage and the current in that branch, and use
the power formulas developed on Page EIGHT 2. Note
that if all the impedances shown in any one of the
circuits in Figure 81 are the same, the power dissipated
in each of those equal impedances is also the same:
one-fourth of the total power dissipated.