microDXP Technical Reference Manual
Version 3.15
October 7, 2019
50
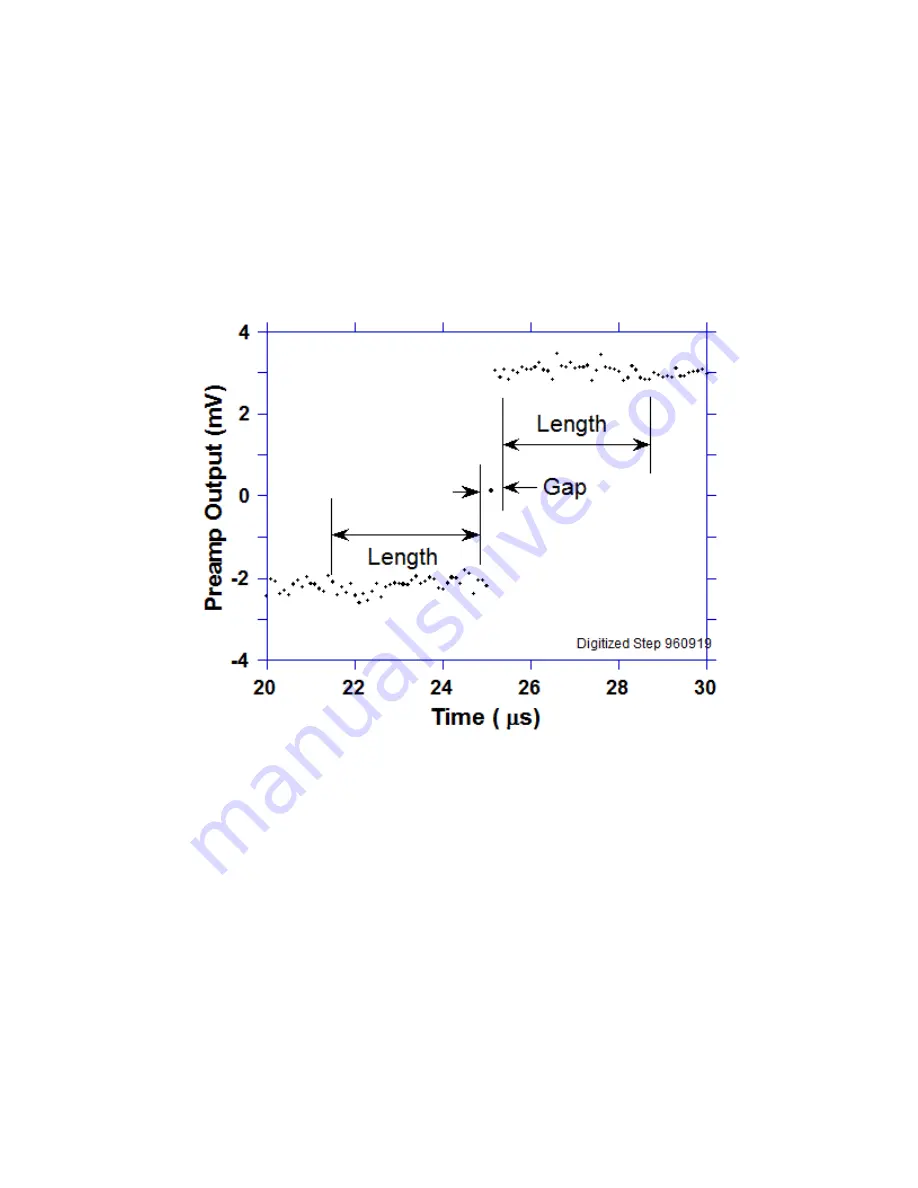
as shown in Figure 4-4, averages are computed over the two regions marked “Length” (the
“Gap” region is omitted because the signal is changing rapidly here), and their difference
taken as a measure of V
x
. Thus the value V
x
may be found from the equation:
𝑉
𝑥,𝑘
= ∑
𝑊
𝑖
𝑖(𝑎𝑓𝑡𝑒𝑟)
𝑉
𝑖
− ∑
𝑊
𝑖
𝑖(𝑏𝑒𝑓𝑜𝑟𝑒)
𝑉
𝑖
Equation 4-2
Where the values of the weighting constants W
i
determine the type of average being
computed. The sums of the values of the two sets of weights must be individually
normalized.
Figure 4-4: Digitized version of one of the x-ray steps of Figure 4.3b.
The primary differences between different digital signal processors lie in two areas: what
set of weights {W
i
} is used and how the regions are selected for the computation of
Equation 4-2. Thus, for example, when the weighting values decrease with separation from
the step, then the equation produces “cusp-like” filters. When the weighting values are
constant, one obtains triangular (if the gap is zero) or trapezoidal filters. The concept
behind cusp-like filters is that, since the points nearest the step carry more information
about its height, they should be more strongly weighted in the averaging process. How one
chooses the filter lengths results in time variant (the lengths vary from pulse to pulse) or
time invariant (the lengths are the same for all pulses) filters. Traditional analog filters are
time invariant. The concept behind time variant filters is that, since the x-rays arrive
randomly and the lengths between them vary accordingly, one can make maximum use of
the available information by adjusting Length on a pulse-by-pulse basis.
In principal, the very best filtering is accomplished by using cusp-like weights and time
variant filter length selection. There are serious costs associated with this approach
however, both in terms of computational power required to evaluate the sums in real time






























