Lancair Columbia 400 Скачать руководство пользователя страница 171 | Manualshive

Страница: 171 / 364

background image

Section 6

Columbia 400 (LC41-550FG)

Weight & Balance

Initial Issue of Manual: November 10, 2004

RC050002

Latest Revision Level/Date: -/11-10-2004

6-13

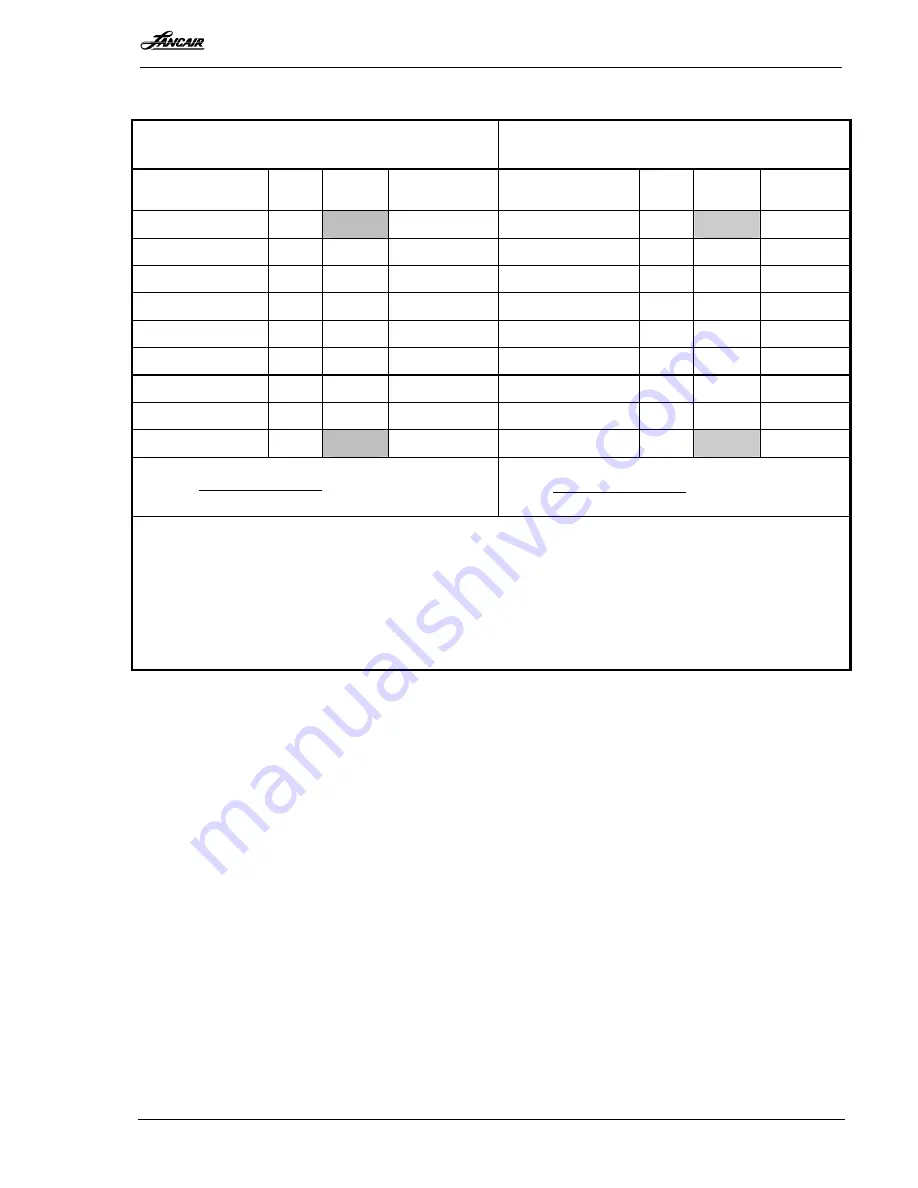
CALCULATOR METHOD

Sample Problem

Calculator Method

Actual Calculation

For This Airplane

ITEM

WT.

(Lbs.)

ARM

(Inches)

MOMENTS

(lbs.-in.)

ITEM

WT.

(Lbs.)

ARM

(Inches)

MOMENTS

(lbs.-in.)

Basic Empty Wt.**

2,485

260,433 Basic Empty Wt.

Front Seat Wts.

380

110.0

41,800 Front Seats

110.0

Rear Seats Wts.

175

141.4

24,745 Rear Seats

141.4

Baggage (Main)

50

166.6

8,330 Baggage (Main)*

166.6

Baggage (Zone A)

0

155.7

0 Baggage (Zone A)*

155.7

Baggage (Zone B)

0

177.4

0 Baggage (Zone B)*

177.4

Baggage (Shelf)

0

199.8

0 Baggage (Aft)

199.8

Fuel (At 6 lbs./gal.)

360

118.0

42,480 Fuel (At 6 lbs./gal.)

118.0

Totals 3,450

377,788 Totals

*When computing baggage moment, use the arm for either the Main Baggage Area, Zone A, or Zones A and B as
applicable. Refer to the Baggage discussion on page 6-10 for more information. In this example, the weight is
evenly distributed over the main baggage area.

**NOTE

The basic empty weight used in this example will vary for each airplane. Refer to the
Weight and Balance Record, which follows Appendix A of this section.

Figure 6 - 13

GRAPHICAL METHOD

The multiplying graphs, which begin on page 6-16, can be used to determine the moments for
each weight location. The answer is not as accurate as doing the calculation with a calculator;
however, the margin of error is not significant and within acceptable parameters of safety. The
example arrows in the graphs on pages 6-16 and 6-17 use the data from the sample problem in
Figure 6 - 13.

When using the multiplying graphs, it is more convenient to divide the moments on the Y or
vertical axis by 1000. For example, 70,000 lbs.-in. is read as 70.0 (x 1000) lbs.-in. Once all the
calculations are made, the answer can then be multiplied by 1000. The numbers shown in Figure
6 - 14 are moment values obtained by reading directly from the graphs and are expressed as 1000
lbs.-in. It should be noted that there is a nominal difference in center of gravity location between
the two procedures.

lbs in

lbs

inches

.

.

.

−

=

inches

lbs

in

lbs

5

.

109

.

450

,

3

.

.

788

,

377

=

−

«
...
169
170
171
172
173
...
»

Содержание Columbia 400

Страница 1: ...REVISED THIS MANUAL CANNOT BE USED FOR FLIGHT OPERATIONS IT IS NOT A SUBSTITUTE FOR THE OFFICIAL FAA APPROVED PILOT S OPERATING HANDBOOK AND AIRPLANE FLIGHT MANUAL The Lancair Company 22550 Nelson Road Bend Municipal Airport Bend Oregon 97701 9710 Phone 541 318 1144 Fax 541 318 1177 CustomerService Lancair com http www lancair com This document meets GAMA Specification No 1 Specification for Pilot...

Страница 2: ......

Страница 3: ...CTIONS SECTION GENERAL 1 LIMITATIONS 2 EMERGENCY PROCEDURES 3 NORMAL PROCEDURES 4 PERFORMANCE 5 WEIGHT BALANCE EQUIPMENT LIST 6 AIRPLANE SYSTEMS DESCRIPTION 7 AIRPLANE HANDLING SERVICE MAINTENANCE 8 SUPPLEMENTS 9 ...

Страница 4: ......

Страница 5: ...OLS 1 6 Airspeed Terminology 1 6 Meteorological Terminology 1 7 Engine Power and Controls Terminology 1 8 Airplane Performance and Flight Planning Terminology 1 9 Weight and Balance Terminology 1 10 REVISIONS AND CONVENTIONS USED IN THIS MANUAL 1 11 Supplements 1 12 Use of the terms Warning Caution and Note 1 12 Meaning of Shall Will Should and May 1 12 Meaning of Land as Soon as Possible or Pract...

Страница 6: ... 141 2 ft 2 13 1 m2 Wing Span 35 8 ft 10 9 m Length 25 2 ft 7 68 m Empty Weight 2500 lbs 1134 kg Gross Weight 3600 lbs 1633 kg Stall Speed 59 KIAS 60 KCAS Maneuvering Speed 158 KIAS 162 KCAS Cruising Speed 181 KIAS 185 KCAS Never Exceed Speed 230 KIAS 235 KCAS Engine 310 HP Continental TSIO 550 C Propeller Hartzell 78 in 198 cm Constant Speed Governor McCauley Note Wingspan is 36 ft with position ...

Страница 7: ...lane including dimensions fuel and oil capacities and certificated weights There are also definitions and explanations of symbols abbreviations and commonly used terminology for this airplane Finally conventions specific to this manual are detailed NOTE Federal Aviation Regulations require that a current Handbook be in the airplane during flight It is the operator s responsibility to maintain the ...

Страница 8: ...ective colors are approved for this airplane 100LL Grade Aviation Fuel Blue 100 Grade Aviation Fuel Green Total Fuel Capacity 106 Gallons 401 L Total Capacity Each Tank 53 Gallons 201 L Total Usable Fuel 49 Gallons 186 L tank 98 Gallons 371 L Total NOTE Under certain atmospheric conditions ice can form along various segments of the fuel system Under these conditions isopropyl alcohol ethylene glyc...

Страница 9: ...g Baggage Weight 120 lbs 54 4 kg TYPICAL AIRPLANE WEIGHTS The empty weight of a typical airplane offered with four place seating standard interior avionics accessories and equipment has a standard empty weight of about 2500 lbs 1134 kg Maximum Useful Load 1100 lbs 499 kg The useful load varies for each airplane Please see Section 6 for specific details CABIN AND ENTRY DIMENSIONS Maximum Cabin Widt...

Страница 10: ...essed in knots TAS True Airspeed is the airspeed of an airplane relative to undisturbed air which is the CAS corrected for altitude temperature and compressibility VH This term refers to the maximum speed in level flight with maximum continuous power VO The maximum operating maneuvering speed of the airplane Do not apply full or abrupt control movements above this speed If a maneuver is entered gr...

Страница 11: ...013 2 mb 4 The temperature gradient from SL to an altitude where the temperature is 56 5 C 69 7 F is 0 00198 C 003564 F per foot and zero above that altitude Standard Temperature Standard Temperature is 15 C 59ºF at sea level pressure altitude and decreases 2 C 3 2 F for each 1000 feet of altitude OAT Outside Air Temperature is the free air static temperature obtained either from in flight tempera...

Страница 12: ... Mixture Control provides a mechanical linkage with the fuel control unit of fuel injection engines to control the size of the fuel feed aperture and thus the air fuel mixture It is also a primary means to shut down the engine Propeller Control The lever used to select a propeller speed Propeller Governor The device that regulates the RPM of the engine and propeller by increasing or decreasing the...

Страница 13: ...he basic gravitational force e g a 1 7 g force GPH Gallons Per Hour is the quantity of fuel consumed in an hour expressed in gallons Limit Load The maximum load a structure is designed to carry and the factor of safety is the percentage of limit load the structure can actually carry before its ultimate load is reached A structure designed to carry a load of 1 000 pounds with a safety factor of 1 5...

Страница 14: ...ter of gravity locations within which the airplane must be operated at a given weight Maximum Empty Weight This is the maximum allowable weight of the airplane when empty before fuel passengers and baggage are added Subtracting the minimum useful load from the maximum gross weight produces the maximum empty weight The amount of additional equipment that can be added to the airplane is determined b...

Страница 15: ... of a lever is the distance in inches between the point at which a force is applied and the fulcrum or the point about which a lever rotates multiplied by the force in pounds Moment is expressed in inch pounds Reference Datum This is an imaginary vertical plane from which all horizontal distances are measured for balance purposes Standard Empty Weight This is the weight of a standard airplane incl...

Страница 16: ...ential to emphasize MEANING OF SHALL WILL SHOULD AND MAY The words shall and will are used to denote a mandatory requirement The word should denotes something that is recommended but not mandatory The word may is permissive in nature and suggests something that is optional MEANING OF LAND AS SOON AS POSSIBLE OR PRACTICABLE The use of these two terms relates to the urgency of the situation When it ...

Страница 17: ... 229 281 231 485 233 690 235 895 238 099 240 304 Example Convert 76 kilograms to pounds Locate the 70 row in the first column and then move right horizontally to Column No 6 and read the solution 167 551 pounds Figure 1 2 CONVERTING POUNDS TO KILOGRAMS Pounds 0 1 2 3 4 5 6 7 8 9 0 0 454 0 907 1 361 1 814 2 268 2 722 3 175 3 629 4 082 10 4 536 4 990 5 443 5 897 6 350 6 804 7 257 7 711 8 165 8 618 2...

Страница 18: ... 399 311 680 314 961 318 241 321 522 324 803 100 328 084 331 365 334 646 337 927 341 207 344 488 347 769 351 050 354 331 357 612 Example Refer to Figure 1 2 and Figure 1 3 for examples of how to use these types of tables Figure 1 4 CONVERTING FEET TO METERS Feet 0 1 2 3 4 5 6 7 8 9 0 0 305 0 610 0 914 1 219 1 524 1 829 2 134 2 438 2 743 10 3 048 3 353 3 658 3 962 4 267 4 572 4 877 5 182 5 486 5 79...

Страница 19: ...38 583 38 976 100 39 370 39 764 40 157 40 551 40 945 41 339 41 732 42 126 42 520 42 913 Example Refer to Figure 1 2 and Figure 1 3 for examples of how to use these types of tables Figure 1 6 CONVERTING INCHES TO CENTIMETERS Inches 0 1 2 3 4 5 6 7 8 9 0 2 54 5 08 7 62 10 16 12 70 15 24 17 78 20 32 22 86 10 25 40 27 94 30 48 33 02 35 56 38 10 40 64 43 18 45 72 48 26 20 50 80 53 34 55 88 58 42 60 96 ...

Страница 20: ...259 417 395 455 732 60 69 111 230 265 426 400 461 741 65 75 120 235 271 435 405 466 750 70 81 130 240 276 444 410 472 759 75 86 139 245 282 454 415 478 769 80 92 148 250 288 463 420 484 778 85 98 157 255 294 472 425 489 787 90 104 167 260 299 482 430 495 796 95 109 176 265 305 491 435 501 806 100 115 185 270 311 500 440 507 815 105 121 194 275 317 509 445 512 824 110 127 204 280 322 519 450 518 83...

Страница 21: ...23 76 23 98 Example Refer to Figure 1 2 and Figure 1 3 for examples of how to use these types of tables Figure 1 9 CONVERTING IMPERIAL GALLONS TO LITERS Imperial Gallons 0 1 2 3 4 5 6 7 8 9 0 0 00 4 55 9 09 13 64 18 18 22 73 27 28 31 82 36 37 40 91 10 45 46 50 01 54 55 59 10 63 64 68 19 72 74 77 28 81 83 86 37 20 90 92 95 47 100 01 104 56 109 10 113 65 118 20 122 74 127 29 131 83 30 136 38 140 93 ...

Страница 22: ... 74 28 00 28 27 28 53 28 79 Example Refer to Figure 1 2 and Figure 1 3 for examples of how to use these types of tables Figure 1 11 CONVERTING U S GALLONS TO LITERS U S Gallons 0 1 2 3 4 5 6 7 8 9 0 0 00 3 79 7 57 11 36 15 14 18 93 22 71 26 50 30 28 34 07 10 37 85 41 64 45 42 49 21 52 99 56 78 60 56 64 35 68 13 71 92 20 75 70 79 49 83 27 87 06 90 84 94 63 98 41 102 20 105 98 109 77 30 113 55 117 3...

Страница 23: ...4 10 115 30 116 50 117 70 118 90 100 120 10 121 30 122 50 123 70 124 90 126 11 127 31 128 51 129 71 130 91 Example Refer to Figure 1 2 and Figure 1 3 for examples of how to use these types of tables Figure 1 13 CONVERTING U S GALLONS TO IMPERIAL GALLONS U S Gallons 0 1 2 3 4 5 6 7 8 9 0 0 00 0 83 1 67 2 50 3 33 4 16 5 00 5 83 6 66 7 49 10 8 33 9 16 9 99 10 82 11 66 12 49 13 32 14 16 14 99 15 82 20...

Страница 24: ...5F 9C 200F 93C 385F 196C 20F 7C 205F 96C 390F 199C 25F 4C 210F 99C 395F 202C 30F 1C 215F 102C 400F 204C 35F 2C 220F 104C 405F 207C 40F 4C 225F 107C 410F 210C 45F 7C 230F 110C 415F 213C 50F 10C 235F 113C 420F 216C 55F 13C 240F 116C 425F 218C 60F 16C 245F 118C 430F 221C 65F 18C 250F 121C 435F 224C 70F 21C 255F 124C 440F 227C 75F 24C 260F 127C 445F 229C 80F 27C 265F 129C 450F 232C 85F 29C 270F 132C 4...

Страница 25: ... two decimal places The table is intended to provide approximate values for converting from one particular quantity of measurement to another Weight Quantity Kg Lbs Converting To U S Gallons Converting To Imperial Gallons Converting To Liters Liters 0 72 1 58 26 of the liter quantity 22 of the liter quantity Imperial Gallons 3 72 7 2 1 2 times the number of Imperial Gallons 4 55 times the number o...

Страница 26: ...Section 1 General Columbia 400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 1 22 Latest Revision Level Date 11 10 2004 This Page Intentionally Left Blank ...

Страница 27: ...rs 2 7 Propeller Blade Angles at 30 Inches Station Pressure 2 7 Weight Limits 2 7 Other Weight Limitations 2 7 Center of Gravity Limits 2 7 Center of Gravity Table 2 8 Maneuvering Limits 2 8 Utility Category 2 8 Approved Acrobatic Maneuvers 2 8 Spins 2 8 Flight Load Factor Limits 2 9 Utility Category 2 9 Kinds of Operation Limits and Pilot Requirements 2 9 Icing Conditions 2 9 Fuel Limitations 2 9...

Страница 28: ...ion 2 Limitations Columbia 400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 2 2 Latest Revision Level Date 11 10 2004 PLACARDS 2 15 General 2 15 Interior Placards 2 15 Exterior Placards 2 21 ...

Страница 29: ... limitations included in this Section These include operating limitations instrument markings and basic placards necessary for the safe operation of the airplane the airplane s engine the airplane s standard systems and the airplane s standard equipment NOTE This section covers limitations associated with the standard systems and equipment in the airplane Refer to Section 9 for amended operating p...

Страница 30: ...d FL250 Decrease 3 5 knots for each 1000 ft above 12 000 feet Press Alt 185 140 181 137 Do not exceed this speed except in smooth air and then only with caution VNE Never Exceed Speed Never Exceed Speed FL250 Decrease 4 4 knots for each 1000 ft above 12 000 feet Press Alt 235 178 230 174 Do not exceed this speed in any operation Figure 2 1 AIRSPEED INDICATOR MARKINGS The airspeed is shown on both ...

Страница 31: ... 40 F 4 C SAE 30 10W30 15W50 or 20W50 Above 40 F 4 C SAE 50 15W50 or 20W50 Oil Temperature Maximum Allowable 240ºF 116 C Recommended takeoff minimum 100 F 38 C Recommended flight operations 170 F to 220 F 76 7 C to 104 4 C Oil Pressures Normal Operations 30 60 psi pounds per square inch Idle minimum 10 psi Maximum allowable cold oil 100 psi Approved Fuel Grades 100LL Grade Aviation Fuel Blue 100 G...

Страница 32: ... In of Hg 15 33 5 In of Hg No Placard 35 5 In of Hg Oil Temperature Minimum for takeoff 100ºF 38 C 220ºF 240ºF 104 C 116 C 100ºF 170ºF 38 C 77 C 170ºF 220ºF 77 C 104 C 240ºF 116 C Oil Pressure Minimum for idle 10 psi N A 10 30 psi and 60 100 psi 30 60 psi 100 psi Cold Oil Fuel Quantity A red line below E or zero indicates the remaining four gallons in each tank cannot be used safely in flight N A ...

Страница 33: ...pounds 9 1 kg When loading baggage in the main baggage compartment Zone A the forward portion of the main baggage area must always be loaded first See page 6 12 for a diagram of loading stations and baggage zones OTHER WEIGHT LIMITATIONS TYPE OF WEIGHT LIMITATION FORWARD DATUM POINT AND WEIGHT AFT DATUM POINT AND WEIGHT VARIATION Minimum Flying Weight Maximum Zero Fuel Weight 105 inches and 2600 l...

Страница 34: ...o it is important to remember that the airplane accelerates quite rapidly in a nose down attitude such as when performing a lazy eight SPINS The intentional spinning of the aircraft is prohibited Flight tests have shown that the aircraft will recover from a one turn spin in less than one additional turn after the application of recovery controls for all points in the weight and balance envelope up...

Страница 35: ... The operational minimum equipment and instrumentation for the kinds of operation are detailed in Part 91 of the FARs ICING CONDITIONS Flight into known icing is prohibited FUEL LIMITATIONS Total Capacity 106 US Gallons 401 L Total Capacity Each tank 53 US Gallons 201 L Total Usable Fuel 49 US Gallons 186 L in each tank 98 US Gallons 371 L Total Maximum Fuel Imbalance 10 US gallons 38 L between le...

Страница 36: ...nt approaches utilizing the GPS receiver must be conducted in the approach mode and Receiver Autonomous Integrity Monitoring RAIM must be available at the Final Approach Fix b Accomplishment of ILS LOC LOC BC LDA SDF MLS or any other type of approach not approved for GPS overlay with the GNS 430 s GPS receiver is not authorized c Use of the GNS 430 VOR ILS receiver to fly approaches not approved f...

Страница 37: ...not relieve the PIC the responsibility to see and avoid traffic and receive appropriate ATC clearance 4 The 400 500 Series Garmin Display Interfaces Pilot s Guide Addendum P N 190 00140 13 Rev A or later revision must be accessible to the flight crew during flight 5 400 500 Series Main software 4 00 or later FAA approved software is required to operate the TIS interface and provide TIS functionali...

Страница 38: ... indication of traffic conflicts with aircraft without transponders 5 Airframe Shadowing Microwave energy can be obstructed by the airframes of both the host and threat aircraft A shadowing occurs when the signals must pass around metal structures a TCAD is designed to operate optimally when the host TCAD antenna and the threat transponder antenna are in line of sight With the TCAD antenna top and...

Страница 39: ...ot established the intruder will not be displayed 9 A poor transponder receiver on the intruder aircraft a geometry where the antennas are shadowed from each other and high traffic density can limit detection range 10 When the host aircraft is above 12 000 feet pressure altitude non Mode C intruders are not tracked OTHER LIMITATIONS Altitude The maximum flight altitude is 25 000 MSL with an FAA ap...

Страница 40: ...Section 2 Limitations Columbia 400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 2 14 Latest Revision Level Date 11 10 2004 This Page Intentionally Left Blank ...

Страница 41: ...ler caps The placards and their locations are shown on the following pages as they appear on the interior and exterior of the airplane INTERIOR PLACARDS On Center Console Below Radios FIRE EXTINGUISHER LOCATED UNDER CO PILOT S SEAT The markings and placards installed in this airplane contain operating limitations that must be complied with when operating this airplane in the Utility category Other...

Страница 42: ...bia 400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 2 16 Latest Revision Level Date A 12 01 2004 Near Pilot and Copilot Interior Door Handles Near Door Handle on Passenger Side On Baggage Compartment Door Joggle ...

Страница 43: ...mitations Initial Issue of Manual November 10 2004 RC050002 Latest Revision Level Date A 12 01 2004 2 17 On Crash Ax In Aft Cabin on Aft Baggage Bulkhead Under Left Rear Seat Next to Leveling Washer Under All Seats On Parking Brake Handle ...

Страница 44: ...ION ABOVE 14 000 FT PA On Center Overhead Console The magnetic direction indicator is calibrated for level flight with the engine radios and strobes operating On Engine Instrument Panel Above Fuel Gauge MAXIMUM FUEL IMBALANCE NOT TO EXCEED 10 GAL On Engine Instrument Panel Above Manifold Pressure Gauge CAUTION MINIMUM 15 MP ABOVE 18 000 FT 158 KIAS 3600 LBS 135 KIAS 2600 LBS VNE 4 4 KIAS 1000 FT V...

Страница 45: ... Revision Level Date A 12 01 2004 2 19 Above Copilot s Fresh Air Vent On Top Center of Engine Instrument Panel when autopilot installed On Engine Instrument Panel Under CHT TIT Gauge On Top Center of Flight Instrument Panel when autopilot installed Near the Left Dimmer Switch on the Pilot s Knee Bolster ...

Страница 46: ...002 Initial Issue of Manual November 10 2004 2 20 Latest Revision Level Date A 12 01 2004 Engraved On Fuel Selector Knob and Upper Plate On Oxygen Distribution Manifold in Forward Overhead Panel On Oxygen Fill Port Set into Hat Shelf LEFT RIGHT OFF OFF ...

Страница 47: ...10 2004 RC050002 Latest Revision Level Date A 12 01 2004 2 21 EXTERIOR PLACARDS On Oil Filler Access Door Near Pilot and Passenger Door Handles On Main Wheel Pants On Nose Gear Wheel Pant or Nose Gear Fairing if nose gear wheel pant not installed On Flaps Near Wing Root Both Sides ...

Страница 48: ...4 Near Fill Cap of Fuel Tank Under Each Wing Near Fuel Drains FOR DRAINING OF WING FUEL SUMP TO OPEN PRESS CUP GENTLY INTO BOTTOM OF VALVE TO DRAIN REQUIRED AMOUNT OF FUEL TO CLOSE REMOVE CUP AND VALVE WILL CLOSE TO DRAIN WING TANKS REFER TO MAINTENANCE MANUAL On Exterior of Gascolator Door Underside of Fuselage On Interior of Gascolator ...

Страница 49: ... Columbia 400 LC41 550FG Limitations Initial Issue of Manual November 10 2004 RC050002 Latest Revision Level Date 11 10 2004 2 23 On Left Side Wing Fillet On Exterior of Fuselage Forward of Wing on Pilot s Side ...

Страница 50: ...0FG RC050002 Initial Issue of Manual November 10 2004 2 24 Latest Revision Level Date A 12 01 2004 On Exterior of Fuselage Forward of Wing on Copilot s Side On Forward Portion of Nose Gear Fairing On Nose Gear Wheel Pant if installed TURN LIMIT ...

Страница 51: ...estart 3 8 Emergency Landing Without Engine Power 3 9 Emergency Landing With Throttle Stuck at Idle Power 3 9 Precautionary Landing With Engine Power 3 10 Engine Driven Fuel Pump EDFP Partial Failure 3 11 Ditching 3 11 Engine Fire On The Ground During Startup 3 12 In Flight Engine Fire 3 12 In Flight Electrical Fire 3 12 In Flight Cabin Fire Fuel Hydraulic Fluid 3 13 In Flight Wing Fire 3 13 Spin ...

Страница 52: ...ain Flight 3 23 Flight Controls Malfunctions 3 23 General 3 23 Aileron or Rudder Failure 3 23 Elevator Failure 3 24 Trim Tab Malfunctions 3 24 Fires 3 25 General 3 25 Engine Fires 3 25 Cabin Fires 3 25 Lightning Strike 3 25 Engine and Propeller Problems 3 26 Engine Roughness 3 26 High Altitude Negative G Loading 3 26 High Cylinder Head Temperatures 3 26 High Oil Temperature 3 26 Low Oil Pressure 3...

Страница 53: ...er 10 2004 RC050002 Latest Revision Level Date 11 10 2004 3 3 Emergency Exit 3 34 General 3 34 Doors 3 34 Seat Belts 3 34 Exiting Cabin Door s Operable 3 34 Exiting Cabin Doors Inoperable 3 34 Inverted Exit Procedures 3 34 General 3 34 Exterior Emergency Exit Release 3 35 Crash Ax 3 36 ...

Страница 54: ...Section 3 Emergency Procedures Columbia 400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 3 4 Latest Revision Level Date 11 10 2004 This Page Intentionally Left Blank ...

Страница 55: ... a crosscheck to ensure that no items are excluded and is used only after control of the airplane is established When the airplane is under control and the demands of the situation permit the Emergency Procedures Checklist should be used to verify that all required actions are completed In all emergencies it is important to communicate with Air Traffic Control ATC or the appropriate controlling en...

Страница 56: ...ed depending on airspeed and height above the ground 6 Left and Right Master Switches SET TO OFF Obtain this airspeed if altitude permits otherwise lower the nose maintain current airspeed and land straight ahead ENGINE FAILURE DURING CLIMB TO CRUISE ALTITUDE Above 400 FT AGL 1 Airspeed 108 KIAS flaps in the up position 2 Fuel Selector SET TO THE FULLER TANK 3 Mixture Control SET TO RICH 4 Backup ...

Страница 57: ...Engine Power checklist 5 2 Engine Restarts Use the Procedures After an Engine Restart checklist NOTE If the engine does not restart and time and altitude permit follow Engine Failure During Flight Below 15 000 ft checklist WARNING At altitudes above 18 000 ft an overrich mixture may result if the turbocharger fails and the engine may stop firing LOSS OF OIL PRESSURE 1 Oil Temperature CHECK WITHIN ...

Страница 58: ...ED ABOUT ONE THIRD 3 Fuel Selector SWITCH TANKS 4 Mixture Control PULL TO LEAN THEN GRADUALLY RICHEN UNTIL ENGINE STARTS 4 1 Engine Does Not Restart 4 1 1 Vapor Suppression SET TO ON 4 1 2 Engine Restarts Use Procedures After an Engine Restart checklist 4 2 Engine Does Not Restart Do Steps 5 and 6 5 Throttle Control SET TO HALF OPEN 6 Backup Boost Pump SET TO ARMED 6 1 Engine Does Not Restart 6 1 ...

Страница 59: ... WITHOUT ENGINE POWER 1 Glide 1 1 Airspeed BEST GLIDE SPEED Figure 3 4 1 2 Propeller Control PULL FULL AFT 1 3 Wing Flaps UP 1 4 Radio MAKE DISTRESS TRANSMISSION Set transponder code 7700 and transmit a Mayday distress condition Give estimated position and intentions 1 5 Seat Belts and Shoulder Harnesses FASTENED AND SECURE 1 6 Loose objects SECURE 1 7 Backup Boost Pump and Vapor Suppression BOTH ...

Страница 60: ...ld be delayed until the pilot is certain that further use of the trim particularly the elevator trim and the flaps are not required 2 Do not open the cabin doors in flight The air loads placed on the doors in flight will damage them and can cause separation from the airplane A damaged or separated door will alter the flight characteristics of the airplane and possibly damage other control surfaces...

Страница 61: ...n high winds and heavy swell conditions approach into the wind In light winds and heavy swell conditions approach parallel to the swell If no swells exist approach into the wind 8 Touchdown Alternatives 8 1 Touchdown Engine power available Maintain minimum descent attitude Apply power to slow or stop descent if necessary When over a suitable touchdown area reduce power and slowly settle into the w...

Страница 62: ...n the ground because of improper starting procedures If circumstances permit move the airplane away from the ground fire by pushing aft on the horizontal stabilizer and then extinguish the ground fire This must only be attempted if the ground fire is small and sufficient ground personnel are present to move the airplane IN FLIGHT ENGINE FIRE 1 Fuel Selector SET TO OFF 2 Throttle Control SET TO CLO...

Страница 63: ...nd deactivate door seals 8 Post Fire Details FOLLOW EMERGENCY LANDING WITHOUT ENGINE POWER CHECKLIST WARNING The fire extinguishing substance is toxic and the fumes must not be inhaled for extended periods After discharging the extinguisher the cabin must be ventilated If oxygen is available put masks on and start oxygen flow Oxygen must only be used after it is determined that the fire is extingu...

Страница 64: ...peller Control INCREASE Higher propeller speeds will mitigate ice accumulation 7 Manifold Pressure MONITOR A drop in manifold pressure may be an indication of induction icing increase throttle settings as required 8 Heated Induction Air SET TO ON Operate if induction icing is evident or suspected 9 Alternate Static Source Open if static source icing is evident or suspected 10 Flight Characteristic...

Страница 65: ...rplane by the input of control forces that override the SpeedBrake failure s Do not under any circumstances re engage a SpeedBrake System that has malfunctioned until the problem is corrected ELECTRICAL SYSTEM OVERCHARGING Both alternators stay on line ammeter shows excessive charge and voltmeter has high voltage indication 1 Defective Alternator Switch SET TO OFF 2 Crosstie Switch SET TO ON 3 Fli...

Страница 66: ...Left Bus Items Right Bus Items Aileron Trim Pitot Heat SpeedBrakes Engine Instruments Carbon Monoxide Detector Oxygen Position Lights Landing Light Left Voltage Regulator Clock and Cabin Fan Strobe Lights Taxi Light Right Voltage Regulator Door Seal Power Point Elevator Trim 4 Depending on which bus failed left or right and the dictates of the current conditions i e day night IMC VMC land the airp...

Страница 67: ...r Switch SET TO OFF If autopilot does not disconnect proceed to step 5 5 Circuit Breaker PULL BREAKER TO THE OFF POSITION MALFUNCTION OF AUTOPILOT AUTOTRIM 1 Flight MANUALLY CONTROL AIRCRAFT AND DISCONNECT AUTOPILOT 2 Trim Circuit Breaker PULL BREAKER TO THE OFF POSITION NOTE If the autopilot suffers an autotrim failure it is permissible to use the autopilot roll axis but do not engage the pitch a...

Страница 68: ...e the unit through the circuit breaker as there is a three minute delay for the CO sensor to stabilize EVACUATING THE AIRPLANE 1 Seat Belts REMOVE Do not remove seat belts until the airplane comes to a complete stop unless there is a compelling reason to do otherwise If the onset of the emergency is anticipated ensure the seat belt is as tight as possible See discussion on page 3 34 2 Doors USE BO...

Страница 69: ...contain items on the left bus the third row contains items on the right bus row four contains essential items and the last row contains the avionics equipment See Figure 7 19 on page 7 61 for a diagram of the electrical system Left Bus Aileron Trim Pitot Heat Speed Brakes Engine Inst CO Detect Oxygen Left Bus Position Lights Landing Lights Left Volt Reg Fan PFD L PWR Right Bus Strobe Lights Taxi L...

Страница 70: ...void obstructions should be attempted If there are no obstructions it is best to land straight ahead unless there is a significant crosswind component Flaps should be applied if airspeed and altitude permit since they can provide a 10 knot reduction in landing speed Engine Failure After Takeoff Above 400 feet AGL With an engine failure after takeoff there may be time to employ modified restarting ...

Страница 71: ...l is not as precisely metered compared to the normal engine driven system and frequent mixture adjustments are necessary when changes are made to the power settings In particular avoid large power changes since an over rich or over lean mixture will affect the proper operation of the engine With a failed engine driven pump full power should be available but power should be reduced below 85 as soon...

Страница 72: ...is less than 5 5 psi In a situation involving a double failure i e a malfunction of the engine driven pump and the latching relay the FUEL annunciator will illuminate Since the primer and backup boost pump are one and the same the pilot can bypass the latching relay by holding the primer switch in the depressed position In this particular situation this would restore engine power and permit contin...

Страница 73: ...s both the time and resources to properly analyze the cause Running the engine until the last practicable moment within the confines of safety is the most prudent course of action It is possible that the throttle may stick at a power setting that is above idle but at insufficient brake horsepower to sustain level flight At the same time this condition may restrict the desired rate of descent In th...

Страница 74: ...ized by sudden and unexplained changes in control forces the trim system switch must immediately be set to the OFF position If the pilot wishes to restore part of the system s trim the following procedure should be used 1 After the trim system switch has been set to OFF the trim circuit breakers elevator and aileron should be pulled to the OFF position 2 Turn the trim system switch to the ON posit...

Страница 75: ...33 Cabin Fires Follow the manufacturer s instructions for use of the fire extinguisher For more information on using the fire extinguisher see the discussion on page 7 136 Once a cabin fire is extinguished it is important to ventilate the cabin as soon as possible The residual smoke and toxins from the fire extinguisher must not be inhaled for extended periods The ventilation system should be oper...

Страница 76: ...gh Altitude Negative G Loading Per the TCM model specification the TSIO 550 Series aircraft engines are not approved for continuous negative or zero g operations Short duration negative g operations such as gust loading will have small or no effect on engine operation Sustained negative g loading at altitudes above 17 000 ft may result in partial or total loss of engine power Engine recovery may r...

Страница 77: ...rated and can be operated but will produce less than its rated horsepower If turbocharger failure occurs before takeoff do not fly the aircraft If a failure occurs in flight readjust mixture as necessary to obtain fuel flow appropriate to manifold air pressure and RPM An interruption in fuel flow or manifold pressure to the engine will result in turbocharger run down At high altitude merely restor...

Страница 78: ...e governor may not be able to get enough oil pressure which causes a delay in propeller responsiveness By the time the propeller responds to earlier governor inputs they have changed resulting in propeller wandering 2 Dirty oil is another cause Contaminants in engine oil cause blockage of close tolerance passages in the governor leading to erratic operations 3 Excessive play in the linkage between...

Страница 79: ...g the electrical load to the system land as soon as possible or as soon as practicable depending on flight conditions All nonessential electrical and avionics equipment must be turned off Over Voltage The voltage regulator is designed to trip the left or right alternator off line in conditions of over voltage i e greater than 16 0 Volts When this happens the annunciator panel will indicate the lef...

Страница 80: ...affects the good bus the crosstie switch should be turned off and only the remaining bus should be used The checklist should be reviewed for items that are on the failed bus and rendered inoperative The table shown in Figure 3 5 lists the equipment driven by each bus Crosstie Switch The crosstie switch is the white switch located between the left and right master switches This switch is to remain ...

Страница 81: ...10 amp 1 amp ESSENTIAL BUS Attitude Horizon Turn Coordinator Panel Lights Annunciators Left Bus Relays Fuel Pump Stall Warning Flaps Right Bus Relays 3 amp 3 amp 7 5 amp 3 amp 5 amp 10 amp 5 amp 10 amp 5 amp BATTERY BUS Nav Com Bypass Switch Hobbs Meter ELT Courtesy Lights 3 amp 3 amp 3 amp 3 amp Figure 3 5 STATIC AIR SOURCE BLOCKAGE The static source for the airspeed indicator the altimeter the r...

Страница 82: ... steady state spin may be encountered if pro spin control inputs are held for 1 turns or more Steady state spins entered above 20 000 feet at heavy weight and aft CG conditions will take the most turns to recover If a steady state spin is entered making and holding the recommended recovery inputs will produce the fastest recovery WARNING The intentional spinning of the aircraft is prohibited WARNI...

Страница 83: ... pitch and or roll axis immediately regain control of the airplane by the input of control forces that override the autopilot s servo s Do not under any circumstances reengage an autopilot that has malfunctioned until the problem is corrected OXYGEN SYSTEM General The oxygen system has built in internal logic to notify the pilot through the aircraft annunciator if any of the following advisory con...

Страница 84: ...ation of the cabin doors in an emergency situation It is important that passengers are familiar with their operation since the pilot may be incapacitated during emergency exiting operations Seat Belts The seat belt should not be removed until the airplane has come to a complete stop unless there are compelling reasons to do otherwise At other times such as when the airplane has come to rest in an ...

Страница 85: ... the pilot to understand the procedures for using the exterior release In some instances the pilot may be incapacitated but conscious and able to offer verbal instructions to ground personnel The following procedures are applicable to exterior removal of the door by ground personnel 1 Open the gascolator compartment by pressing the two spring buttons 2 Move the door latching mechanism of the pilot...

Страница 86: ...the window near the doorframe Several smart blows to the window area around the perimeter of the doorframe will remove enough pieces so that the middle portion of the window can be removed with a few heavy blows Once the major portion of the window is removed and if time and circumstances permit use the ax blade to smooth down the jagged edges around the doorframe This will minimize injury when eg...

Страница 87: ... 4 10 Crosstie Operation 4 11 SpeedBrake Ground Operations 4 11 Autopilot Autotrim Operations 4 11 Before Taxi 4 12 Taxiing 4 12 Before Takeoff 4 12 Minor Spark Plug Fouling 4 14 Normal Takeoff 4 14 Short Field Takeoff 4 14 Crosswind Operations 4 15 Normal Climb 4 15 Maximum Performance Climb 4 15 Cruise 4 15 Descent 4 16 Expedited Descent 4 16 Before Landing 4 16 Normal Landing 4 17 Short Field L...

Страница 88: ...t Table 4 25 Taxiing 4 25 Before Takeoff 4 26 Engine Temperatures 4 26 Engine Runup 4 26 Door Seals 4 26 Takeoffs 4 26 Normal Takeoff 4 26 Short Field Takeoff 4 27 Crosswind Takeoff 4 27 Normal and Maximum Performance Climbs 4 27 Best Rate of Climb Speeds 4 27 Cruise Climb 4 27 Best Angle of Climb Speeds 4 27 Power Settings 4 28 Vapor Suppression 4 28 Normal Operations above 18 000 Ft 4 28 Cruise ...

Страница 89: ...dures Initial Issue of Manual November 10 2004 RC050002 Latest Revision Level Date 11 10 2004 4 3 Practicing Stalls 4 32 Loading and Stall Characteristics 4 33 Spins 4 33 Cold Weather Operations 4 33 Hot Weather Operations 4 35 Noise Abatement 4 36 ...

Страница 90: ...Section 4 Normal Procedures Columbia 400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 4 4 Latest Revision Level Date 11 10 2004 This Page Intentionally Left Blank ...

Страница 91: ... Field Takeoff to 50 feet Flaps Setting Up Position Takeoff Position Airspeed 110 KIAS 80 KIAS Climb To Altitude Normal Best Engine Cooling Best Rate of Climb at Sea Level Best Rate of Climb at 10 000 Feet Best Angle of Climb at Sea Level Best Angle of Climb at 10 000 Feet Flaps Setting Up Position Up Position Up Position Up Position Up Position Airspeed 110 KIAS 110 KIAS 110 KIAS 82 KIAS 86 KIAS ...

Страница 92: ...e Cabin 1 Pitot Tube Cover REMOVE AND STORE 2 Required Aircraft Documents AVAILABLE IN THE AIRPLANE 3 Ignition Switch SET TO OFF 4 Mixture SET TO IDLE CUTOFF 5 Avionics Master Switch SET TO OFF 6 Crosstie Switch SET TO OFF 7 Left Battery Switch ON Press right side of split rocker switch 8 Right Battery Switch ON Press right side of split rocker switch 9 Trim System Switch CHECK SET TO THE ON POSIT...

Страница 93: ...K FOR INSTALLATION AND CONDITION 6 Wing Tip CHECK Look for damage check security of position and anti collision lights Area 3 Left Wing Leading Edge Fuel Tank Left Tire 1 Leading Edge CHECK Look for damage 2 Fuel Vent CHECK FOR OBSTRUCTIONS 3 Landing Light CHECK Look for lens cracks and check security 4 Fuel Quantity CHECK VISUALLY AND SECURE FILLER CAP 5 Wing Fuel Drain CHECK FOR CONTAMINATION Pr...

Страница 94: ... of fuselage between the cabin door and the horizontal stabilizer 8 Antennas Bottom of Fuselage CHECK FOR SECURITY Area 7 Tail Section 1 Leading Edge of Horizontal and Vertical Surfaces CHECK Look for damage 2 Antennas Vertical Stabilizer CHECK FOR SECURITY 3 Rudder Elevator Hardware CHECK General condition and security 4 Rudder Surface CHECK freedom of movement 5 Fixed Elevator Surfaces CHECK SEC...

Страница 95: ...r a cold engine HOT ENGINE mixture out run vapor suppression for 1 minute then perform normal start 9 Throttle Control CLOSED AND THEN OPEN 1 8 INCH to 1 4 INCH 10 Check Propeller Area CLEAR Ensure people equipment are not in the propeller area 11 Ignition Switch TURN TO START POSITION 12 Ammeter MONITOR Both left and right batteries should discharge the same amount during start CAUTION If no oil ...

Страница 96: ...T POSITION CAUTION If the engine starter is engaged for 30 seconds and the engine will not start release the starter switch and allow the starter motor to cool for three to five minutes Release the starter as soon as the engine fires Never engage the starter while the propeller is still turning CAUTION The master switches should not be turned on until after the engine has started and the ground po...

Страница 97: ...N POSITION Ensure SpeedBrakeTM annunciator is off and both SpeedBrakesTM are retracted NOTE The SpeedBrake system should be functionally checked for proper operation prior to flight The independent electrical clutches need to be synchronized by SpeedBrake activation before flight and or after SpeedBrake circuit breaker pull If the SpeedBrakes remain slightly extended it indicates SpeedBrake failur...

Страница 98: ...s played 8 Acknowledge Switch PRESS OFF Ensure aural warning stops 9 Fuel Selector Valve SET TO FULLER TANK 10 Autopilot Master Switch READY POSITION See Section 9 for preflight and functional checks The autopilot should be in the Ready state but not engaged 11 Cabin Doors CLOSED AND LATCHED Verify that red annunciator door light is off 12 Passenger Side Door Lock IN THE UNLOCKED POSITION 13 Engin...

Страница 99: ... engine might start and cause death or injury This type of malfunction must be corrected before operating the engine CAUTION Do not underestimate the importance of pre takeoff magneto checks When operating on single ignition some RPM drop should always occur Normal indications are 25 to 75 RPM and a slight engine roughness as each magneto is switched off A drop in excess of 150 RPM may indicate a ...

Страница 100: ...nd require engine inspection NORMAL TAKEOFF 1 Landing Taxi Lights AS REQUIRED 2 Mixture FULL RICH 3 Power ADVANCE SLOWLY TO FULL RPM 2600 RPM Watch manifold pressure for indication of overboost 4 Elevator Control LIFT NOSE AT 64 74 KIAS 5 Climb Speed ACCELERATE TO BEST RATE OF CLIMB SPEED OF 110 KIAS 6 Wing Flaps RETRACT At 400 feet AGL and at or above the best rate of climb speed 7 Landing Taxi L...

Страница 101: ...0 0 to 33 5 inches of Hg 2 Propeller Control SET AS APPROPRIATE TO ACHIEVE 65 TO 85 POWER 2100 to 2500 RPM 3 Mixture LEAN AS REQUIRED Use TIT gauge to set 1650 F or performance charts in Section 5 Above 65 power only rich of peak operation is permitted 4 Backup Boost Pump NOT ARMED 5 Changing Fuel Tanks PERFORM STEPS 5 1 AND 5 2 5 1 Vapor Suppression SET TO ON DURING FUEL TANK CHANGEOVERS 5 2 Fuel...

Страница 102: ...ol and then decrease RPM with the propeller control When engine temperatures have stabilized lean mixture to desired TIT WARNING Continuous overboost operation may damage the engine and require engine inspection DESCENT 1 Fuel Selector Valve SET TO RIGHT OR LEFT as appropriate 2 Power Settings AS REQUIRED 3 Mixture MOVE TO RICHER SETTING AS REQUIRED 4 Backup Boost Pump NOT ARMED 5 Vapor Suppressio...

Страница 103: ... 4 Maximum Full Flaps Airspeed 117 KIAS 5 Minimum Approach Speed with Wing Flaps in Landing Position 80 KIAS 6 Trim Tabs 2 ADJUST AS REQUIRED 7 Power REDUCE AT THE FLARE POINT 8 Touchdown MAIN WHEELS FIRST 9 Landing Roll LOWER NOSE WHEEL SMOOTHLY AND QUICKLY 10 Braking and Flaps APPLY HEAVY BRAKING AND RETRACT FLAPS Up position BALKED LANDING Go Around 1 Power SET THROTTLE TO FULL At 2600 RPM 2 Sp...

Страница 104: ...down 6 Trim Tabs 2 SET ALL TO NEUTRAL 7 Avionics Master Switch SET TO OFF Ensure MFD is ready for shutdown 8 All Electrical Equipment SET TO OFF Check that all rocker switches are down 9 Nav Com Bypass Switch SET TO OFF 10 Mixture SET TO IDLE CUTOFF 11 Ignition Switch SET TO OFF after engine stops 12 Left and Right Master Switches SET TO OFF CAUTION Allow the engine to idle at 900 RPM for 5 minute...

Страница 105: ...inspection it is unlikely that an uninformed passenger will use them as a step Aileron Servo Tab The aileron servo tab on the trailing edge of the left aileron assists in movement of the aileron The servo tab is connected to the aileron in a manner that causes the tab to move in a direction opposite the movement of the aileron The increased aerodynamic force applied to the tab helps to move the ai...

Страница 106: ...d then the selector handle is not properly seated in the detent In addition if the fuel selector is not seated or is in the OFF position a red FUEL VALVE indication is displayed on the annunciator panel FUEL QUANTITY The Columbia 400 fuel quantity measuring system described on page 7 52 provides a fairly accurate indication of the onboard fuel The system has two sensors in each tank and flat spots...

Страница 107: ...light Flight without the wicks can cause the loss of or problems with communications and navigation See Section 7 page 7 137 for more information BEFORE STARTING ENGINE Fresh Air Vents The fresh air eyeball vents for all unoccupied seats shall be closed when the pilot is the only person in the airplane This is because in the event of an engine fire all ventilation must be turned off Turning off in...

Страница 108: ...n adjustable lap shoulder combination would be In fact use of the lap belt alone has been associated with a number of different injuries According to the AOP the least desirable alternative is to put the shoulder strap under one arm ENGINE STARTING Normal Starting Under normal conditions there should be no problems with starting the engine The most common pilot mistake is over priming of the engin...

Страница 109: ...it is too high The master switches must be turned off before removing the ground power plug If the master switches are turned on before the ground power plug is removed the cables going to the plug will stay energized CAUTION The ammeter must be monitored when recharging the batteries as damage to the batteries can occur if the voltage from the ground power unit is too high Right Battery Inoperati...

Страница 110: ... Federal Aviation Regulations require each passenger to use the installed restraint devices during taxi takeoff and landing Use of the three point restraint system is accomplished by grasping the male end of the buckle drawing the lap webbing and diagonal harness across the lower and upper torso and inserting it into the female end of the buckle There is a distinctive snap when the two parts are p...

Страница 111: ...g Headwind Right Wing Aileron Up Move Aileron Control to the Right Neutral Hold Elevator Control in Neutral Position Left Quartering Tailwind Left Wing Aileron Down Move Aileron Control to the Right Down Elevator Move Elevator Control Forward Right Quartering Tailwind Right Wing Aileron Down Move Aileron Control to the Left Down Elevator Move Elevator Control Forward Figure 4 4 TAXIING The first t...

Страница 112: ...e instruments to verify that all indications are within normal limits Operation of the left and right buses should be checked This can be done by turning off each bus individually and ensuring that the essential and avionics buses are energized then turning on the crosstie switch and ensuring the ammeter shows a charge for the left and right batteries Door Seals The door seal switch is not turned ...

Страница 113: ...in alignment over the runway and in the climb out corridor Maintain the best angle of climb speed 82 to 86 KIAS until the airplane is clear of all obstacles Once past all obstacles accelerate to the best rate of climb speed 110 KIAS at or above 400 feet AGL raise the flaps NORMAL AND MAXIMUM PERFORMANCE CLIMBS Best Rate of Climb Speeds The normal climb speed of the airplane 110 KIAS produces the m...

Страница 114: ...n Vapor Suppression The vapor suppression rocker switch must be turned on in the following situations Operations above 18 000 ft If TIT is rising above 1460ºF at full power with the mixture full rich at any altitude Once engine temperatures have stabilized and if the aircraft is below 18 000 ft the vapor suppression switch may be turned off The vapor suppression switch should also be turned on any...

Страница 115: ...ue If this occurs the pilot may wish to use the most conservative higher number for leaning the engine At power settings below 85 power starting at full rich mixture lean slowly while observing the TIT When changing the mixture to lean of peak it is acceptable to have TIT indications temporarily in the yellow range but indications must return to the normal range upon leaning completion Best power ...

Страница 116: ...normal indications and to systematically increase mixture settings as altitude is decreased The descent from altitude is best performed through gradual power reductions and gradual enrichment of the mixture Avoid long descents at low manifold pressure as the engine can cool excessively and may not accelerate properly when power is reapplied If long rapid descents are made the speed brakes if insta...

Страница 117: ...ns are performed with the flaps set to the landing position The landing approach speed is 85 to 90 KIAS depending on gross weight and wind conditions The approach can be made with or without power however power should be reduced to idle before touchdown The use of forward and sideslips are permitted if required to dissipate excess altitude Remember that the slipping maneuver will increase the stal...

Страница 118: ...r heavy braking especially when the airplane is near gross weight allow the brakes to cool for about 20 minutes before additional heavy braking The brakes may overheat if there is repeated heavy braking without adequate cooling time SHUTDOWN The engine should be idled at 900 RPM for five minutes minimum after landing part of this may be taxi time in order to give the turbochargers time to cool dow...

Страница 119: ...a forward CG and fairly benign stall characteristics It is recommended during the checkout and indoctrination phase for the Columbia 400 LC41 550FG that the pilot investigates stall performance at near gross weight with a CG towards the aft limit of the envelope This training of course should be under the supervision of a qualified and certificated flight instructor SPINS The airplane as certified...

Страница 120: ...superficial preheating Apply the hot air primarily to the oil sump filter and cooler area for 15 to 30 minutes and turn the propeller by hand through six to eight revolutions at 5 to 10 minute intervals Periodically feel the top of the engine and when some warmth is noted apply heat directly to the upper portion of the engine for five minutes to heat the fuel lines and cylinders This will ensure p...

Страница 121: ... is SAE 30 10W30 15W50 or 20W50 In case of temporary cold weather consideration should be given to hangaring the airplane between flights HOT WEATHER OPERATIONS Flight operations during hot weather usually present few problems It is unlikely that ambient temperatures at the selected cruising altitude will be high enough to cause problems The airplane design provides good air circulation under norm...

Страница 122: ...ations do all that is possible to mitigate the impact of noise on the environment In some instances the noise levels of small airplanes operating at smaller general aviation airfields are more noticeable This is because at larger airports with frequent large airplane activity there is an expectation of airplane ambient noise The general aviation pilot can enhance the opinion of the general public ...

Страница 123: ...itude 5 14 Cruise Performance 2000 Ft Pressure Altitude 5 15 Cruise Performance 4000 Ft Pressure Altitude 5 16 Cruise Performance 6000 Ft Pressure Altitude 5 17 Cruise Performance 8000 Ft Pressure Altitude 5 18 Cruise Performance 10000 Ft Pressure Altitude 5 19 Cruise Performance 12000 Ft Pressure Altitude 5 20 Cruise Performance 14000 Ft Pressure Altitude 5 21 Cruise Performance 16000 Ft Pressure...

Страница 124: ...fluence actual results Fuel consumption assumes proper leaning of the mixture and control of the power settings The combined effect of these variables may produce differences as great as 10 The pilot must apply an appropriate margin of safety in terms of estimated fuel consumption and other performance aspects such as takeoff and landing Fuel endurance data include a 45 minute reserve at the speci...

Страница 125: ...0 220 230 240 250 Knots Calibrated Airspeed KCAS Knots Indicated Airspeed KIAS Figure 5 2 Airspeed Calibration Normal and Alternate Static Source Flaps Takeoff Position 12 50 60 70 80 90 100 110 120 130 140 50 60 70 80 90 100 110 120 130 140 Knots Calibrated Airspeed KCAS Knots Indicated Airspeed KIAS Figure 5 3 Example 157 KIAS is equal to 152 KCAS when using the alternate static source Alternate...

Страница 126: ...30 50 60 70 80 90 100 110 120 130 Knots Calibrated Airspeed KCAS Knots Indicated Airspeed KIAS Figure 5 4 Equivalent Airspeed Calibration 12 000 ft 140 150 160 170 180 190 200 210 220 230 240 250 260 270 140 150 160 170 180 190 200 210 220 230 240 250 260 270 Knots Equivalent Airspeed KEAS Knots Calibrated Airspeed KCAS Figure 5 5 Example 70 KIAS is equal to 71 KCAS when using the normal static so...

Страница 127: ... 2004 RC050002 Latest Revision Level Date 11 10 2004 5 5 Equivalent Airspeed Calibration 18 000 ft 140 150 160 170 180 190 200 210 220 230 240 250 260 270 140 150 160 170 180 190 200 210 220 230 240 250 260 270 Knots Equivalent Airspeed KEAS Knots Calibrated Airspeed KCAS Figure 5 6 ...

Страница 128: ... speeds are established using maximum gross weight and the most forward center of gravity CG i e 3600 pounds with the CG located 108 8 inches from the datum This configuration will produce a higher stalling speed when compared with the speed that would result from a more rearward CG or a lesser gross weight at the same CG While an aft CG lowers the stalling speed of the airplane the benign stallin...

Страница 129: ... 94 3600 lbs 1633 kg Flaps Landing 59 60 64 65 70 72 83 85 Figure 5 8 SPEEDBRAKES When SpeedBrakes are installed it is important to be aware of the following performance changes that may result when the speed brakes are deployed 1 During takeoff with the SpeedBrakes inadvertently deployed expect an extended takeoff roll and reduction in rate of climb until the SpeedBrakes are retracted 2 During cr...

Страница 130: ... 5 2 5 2 4 3 4 4 3 4 3 5 2 5 1 10 2 10 3 9 5 9 6 8 8 6 9 5 9 3 10 2 15 3 15 5 14 7 13 10 11 11 10 13 8 14 5 15 3 20 3 20 7 19 10 17 13 15 15 13 17 10 19 7 20 3 25 4 25 9 23 12 22 16 19 19 16 22 13 23 9 25 4 30 5 30 10 28 15 26 19 23 23 19 26 15 28 10 30 5 35 6 34 12 33 17 30 22 27 27 22 30 18 33 12 34 6 WIND VELOCITY KNOTS 40 7 39 14 38 20 35 26 31 31 26 35 20 38 14 39 7 This table is used to dete...

Страница 131: ...Figure 5 11 Headwind Component 10 Knots Ground Roll 1400 ft 427 m 50 ft Obstacle 2050 ft 625 m Runway Slope Correction Add 1 to ground roll for every 0 1 0 2 of uphill slope For operation on a known level smooth mowed grass runway which is either wet or dry but does not include standing water the ground roll distance obtained from this landing performance chart must be multiplied by a factor of 1 ...

Страница 132: ...hould be used in conjunction with the takeoff distance chart in Figure 5 10 to determine the proper takeoff speed based on aircraft weight Takeoff Speed Schedule 60 65 70 75 80 85 90 95 2800 2900 3000 3100 3200 3300 3400 3500 3600 3700 Takeoff Weight lb Speed KIAS Speed at 50 ft obstacle For Short Field Takeoff Speed at Rotation Speed at 50 ft obstacle For Normal Takeoff Figure 5 11 ...

Страница 133: ...0 1635 1225 1790 1515 1141 1655 1400 1055 8000 1935 1635 1220 1795 1515 1140 1655 1400 1050 9000 1935 1635 1220 1795 1515 1140 1655 1400 1050 10000 1935 1635 1220 1795 1515 1135 1655 1400 1050 11000 1940 1635 1215 1800 1515 1135 1660 1400 1045 12000 1940 1635 1215 1800 1517 1132 1660 1400 1045 13000 1940 1635 1210 1790 1506 1120 1650 1390 1035 14000 1945 1635 1210 1780 1495 1110 1640 1380 1025 150...

Страница 134: ...110 1326 12 2 7 3 27 6 25 16000 110 1350 11 5 6 9 26 1 24 15000 110 1368 10 7 6 4 24 2 22 14000 110 1382 10 0 6 0 22 7 20 13000 110 1392 9 3 5 6 21 2 19 12000 110 1398 8 6 5 1 19 3 17 11000 110 1402 7 8 4 7 17 8 16 10000 110 1404 7 1 4 3 16 3 14 9000 110 1404 6 4 3 9 14 8 13 8000 110 1403 5 7 3 4 12 9 11 7000 110 1401 5 0 3 0 11 4 10 6000 110 1399 4 3 2 6 9 8 8 5000 110 1398 3 6 2 1 7 9 7 4000 110...

Страница 135: ...s operating horsepowers Between 65 and 85 of brake horsepower the mixtures should be leaned through use of the turbine inlet temperature TIT gauge Please refer to page 4 29 in this handbook for proper leaning techniques KTAS values in the tables are valid without the nose wheel pant installed If the nose wheel pant is installed add 4 kts to the KTAS values The maximum recommended cruise setting is...

Страница 136: ... 64 61 55 45 23 21 20 18 16 16 14 12 23 21 20 18 16 15 14 12 22 21 19 18 16 15 14 12 87 81 77 69 62 59 53 47 87 79 75 68 62 59 53 44 83 80 73 67 61 58 53 45 182 178 176 170 164 161 154 146 182 177 175 170 164 161 154 143 180 178 173 168 163 160 154 143 76 71 68 62 56 53 46 39 75 70 67 62 55 52 46 36 73 71 66 60 55 52 46 36 20 18 17 16 14 13 12 10 20 18 17 16 14 13 12 10 19 18 17 15 14 13 12 10 75 ...

Страница 137: ... 64 61 55 45 23 21 20 18 16 16 14 12 23 21 20 18 16 15 14 12 22 21 19 18 16 15 14 12 87 81 77 69 62 59 53 47 87 79 75 68 62 59 53 44 83 80 73 67 61 58 53 45 185 182 179 173 167 164 157 149 185 180 178 173 167 164 157 145 183 181 176 172 166 163 157 146 76 71 68 62 56 53 46 39 75 70 67 62 55 52 46 36 73 71 66 60 55 52 46 36 20 18 17 16 14 13 12 10 20 18 17 16 14 13 12 10 19 18 17 15 14 13 12 10 75 ...

Страница 138: ... 12 22 21 19 18 16 15 14 12 87 81 77 69 62 59 53 47 87 79 75 68 62 59 53 44 83 80 73 67 61 58 53 45 189 185 182 177 170 167 160 152 188 184 181 176 170 167 160 148 186 184 180 175 169 166 160 149 76 71 68 62 56 53 46 39 75 70 67 62 55 52 46 36 73 71 66 60 55 52 46 36 20 18 17 16 14 13 12 10 20 18 17 16 14 13 12 10 19 18 17 15 14 13 12 10 75 69 66 60 54 51 45 40 74 68 65 59 53 51 45 37 71 68 63 58 ...

Страница 139: ...64 61 55 45 23 21 20 18 16 16 14 12 23 21 20 18 16 15 14 12 22 21 19 18 16 15 14 12 87 81 77 69 62 59 53 47 87 79 75 68 62 59 53 44 83 80 73 67 61 58 53 45 192 188 186 180 173 170 163 155 192 187 185 179 173 170 163 151 190 188 183 178 172 169 163 151 76 71 68 62 56 53 46 39 75 70 67 62 55 52 46 36 73 71 66 60 55 52 46 36 20 18 17 16 14 13 12 10 20 18 17 16 14 13 12 10 19 18 17 15 14 13 12 10 75 6...

Страница 140: ...23 22 20 18 17 16 14 12 90 83 79 71 64 60 54 48 90 82 78 70 63 60 54 45 86 82 75 69 63 60 54 45 199 195 192 186 179 175 168 159 199 194 191 185 178 175 168 155 197 194 189 184 178 174 167 156 76 71 68 62 56 53 46 39 75 70 67 62 55 52 46 36 73 71 66 60 55 52 46 36 20 19 18 16 14 14 12 11 20 18 18 16 14 14 12 10 19 19 17 16 14 13 12 10 77 71 68 61 55 52 46 40 77 70 66 60 54 52 46 38 73 70 65 59 54 5...

Страница 141: ... 69 64 61 55 45 24 22 21 19 17 16 14 13 24 22 21 19 17 16 14 12 23 22 20 18 17 16 14 12 90 83 79 71 64 60 54 48 90 82 78 70 63 60 54 45 86 82 75 69 63 60 54 45 204 199 196 189 182 178 171 163 203 198 195 188 182 178 171 159 201 198 193 187 181 178 171 159 76 71 68 62 56 53 46 39 75 70 67 62 55 52 46 36 73 71 66 60 55 52 46 36 20 19 18 16 14 14 12 11 20 18 18 16 14 14 12 10 19 19 17 16 14 13 12 10 ...

Страница 142: ...69 64 61 55 45 24 22 21 19 17 16 14 13 24 22 21 19 17 16 14 12 23 22 20 18 17 16 14 12 90 83 79 71 64 60 54 48 90 82 78 70 63 60 54 45 86 82 75 69 63 60 54 45 207 203 199 193 186 182 174 166 207 201 198 192 185 182 174 162 204 202 196 191 184 181 174 163 76 71 68 62 56 53 46 39 75 70 67 62 55 52 46 36 73 71 66 60 55 52 46 36 20 19 18 16 14 14 12 11 20 18 18 16 14 14 12 10 19 19 17 16 14 13 12 10 7...

Страница 143: ...2 173 211 206 204 199 193 189 182 169 209 207 203 198 192 189 182 170 85 80 77 71 65 62 55 48 84 79 76 71 64 61 55 45 82 80 75 69 64 61 55 45 24 22 21 19 17 16 14 13 24 22 21 19 17 16 14 12 23 22 20 18 17 16 14 12 91 85 80 72 65 61 54 48 91 83 79 71 64 61 54 45 87 84 77 70 63 60 54 45 212 208 205 198 191 187 179 169 211 206 204 197 191 187 179 165 209 207 202 196 190 186 178 165 76 71 68 62 56 53 ...

Страница 144: ...7 178 215 211 209 203 197 194 187 174 213 212 207 202 196 193 187 175 85 80 77 71 65 62 55 48 84 79 76 71 64 61 55 45 82 80 75 69 64 61 55 45 24 22 21 19 17 16 14 13 24 22 21 19 17 16 14 12 23 22 20 18 17 16 14 12 91 85 80 72 65 61 54 48 91 83 79 71 64 61 54 45 87 84 77 70 63 60 54 45 216 212 209 203 196 192 184 175 216 211 208 202 196 192 184 171 214 212 207 201 195 191 184 171 76 71 68 62 56 53 ...

Страница 145: ...2 185 217 213 211 206 201 198 192 182 215 214 210 205 200 198 192 182 85 80 77 71 65 62 55 48 84 79 76 71 64 61 55 45 82 80 75 69 64 61 55 45 25 23 22 20 18 17 15 14 24 22 21 19 18 17 15 13 23 22 21 19 17 17 15 13 95 87 83 76 68 64 57 53 91 83 79 72 68 64 57 49 87 83 79 72 64 64 57 49 219 216 213 208 202 198 191 184 219 214 212 207 201 198 191 180 217 215 211 206 200 197 191 180 76 71 68 62 56 53 ...

Страница 146: ...5 188 221 216 214 209 204 201 195 185 219 217 213 208 203 201 195 185 85 80 77 71 65 62 55 48 84 79 76 71 64 61 55 45 82 80 75 69 64 61 55 45 25 23 22 20 18 17 15 14 24 22 21 19 18 17 15 13 23 22 21 19 17 17 15 13 93 86 82 74 67 64 57 51 92 84 80 73 66 63 57 49 89 85 78 72 66 63 57 49 222 219 216 211 205 201 195 188 222 218 215 210 204 201 195 184 220 218 214 209 203 201 195 185 76 71 68 62 56 53 ...

Страница 147: ...0 193 226 221 219 214 209 206 200 190 224 222 218 213 208 205 199 190 85 80 77 71 65 62 55 48 84 79 76 71 64 61 55 45 82 80 75 69 64 61 55 45 25 23 22 20 18 17 15 14 24 22 21 19 18 17 15 13 23 22 21 19 17 17 15 13 93 86 82 74 67 64 57 51 92 84 80 73 66 63 57 49 89 85 78 72 66 63 57 49 228 224 221 216 210 206 200 193 227 223 220 215 209 206 200 189 225 223 219 214 208 206 200 190 76 71 68 62 56 53 ...

Страница 148: ...5 198 228 224 223 219 214 211 205 195 226 225 222 218 213 211 205 195 85 80 77 71 65 62 55 48 84 79 76 71 64 61 55 45 82 80 75 69 64 61 55 45 25 23 22 20 18 17 15 14 24 22 21 19 18 17 15 13 23 22 21 19 17 17 15 13 93 86 82 74 67 64 57 51 92 84 80 73 66 63 57 49 89 85 78 72 66 63 57 49 232 229 226 221 216 212 206 198 232 228 226 221 215 212 206 194 230 228 224 220 215 212 205 194 76 71 68 62 56 53 ...

Страница 149: ...8 201 231 227 226 221 217 214 208 197 229 228 224 221 216 213 208 198 85 80 77 71 65 62 55 48 84 79 76 71 64 61 55 45 82 80 75 69 64 61 55 45 25 23 22 20 18 17 15 14 24 22 21 19 18 17 15 13 23 22 21 19 17 17 15 13 93 86 82 74 67 64 57 51 92 84 80 73 66 63 57 49 89 85 78 72 66 63 57 49 235 232 229 224 218 215 208 200 235 231 228 224 218 215 208 196 233 231 227 222 217 214 208 197 76 71 68 62 56 53 ...

Страница 150: ...GE NAUTICAL MILES ALTITUDE FEET 85 80 75 70 65 60 55 45 Figure 5 28 Conditions 3600 lbs 1633 kg Max Gross Weight Standard Temperature Proper Leaning Full Fuel Tanks 98 Gallons 371 L Assumptions Chart assumes applicable BHP is maintained to maximum flight altitude Note The chart includes fuel for starting the engine taxi takeoff and climb to altitude The 45 minute reserve allowance is based on the ...

Страница 151: ...E FEET 85 80 75 70 65 60 55 45 Figure 5 29 Conditions 3600 lbs 1633 kg Max Gross Weight Standard Temperature Proper Leaning Full Fuel Tanks 98 Gallons 371 L Assumptions Chart assumes applicable BHP is maintained to maximum flight altitude Note The chart includes fuel for starting the engine taxi takeoff and climb to altitude The 45 minute reserve allowance is based on the applicable percentage of ...

Страница 152: ...s based on a fuel consumption of 9 GPH 34 1 LPH and is included here to provide a general familiarization overview Under actual conditions most pilots can perform the calculation for fuel used or the available holding time without reference to the graph Moreover the graph is only an approximation of the average anticipated fuel consumption There will be wide variability under actual conditions In ...

Страница 153: ...ance data numbers for the field elevation data from the cruise altitude Pressure Altitude Descent Speed KIAS Rate of Descent FPM Fuel Flow GPH LPH Time Min Fuel Used Gal L Distance NM 25000 159 500 19 0 72 0 0 0 0 0 0 24000 160 500 18 8 71 2 2 0 1 4 8 23000 161 500 18 6 70 4 4 0 1 4 16 22000 161 500 18 3 69 3 6 0 2 8 24 21000 162 500 18 1 68 5 8 0 2 8 32 20000 163 500 17 9 67 8 10 0 3 11 39 19000 ...

Страница 154: ...ponent 10 Braking Maximum Ground Roll 1240 ft 378 m 50 ft Obstacle 2600 ft 793 m Runway Slope Correction Add 1 to ground roll for every 0 1 0 2 of downhill slope For operation on a known level smooth mowed grass runway which is either wet or dry but does not include standing water the ground roll distance obtained from this landing performance chart must be multiplied by a factor of 1 6 to obtain ...

Страница 155: ...h the landing distance chart in Figure 5 32 to determine the proper landing speed based on aircraft weight Landing Speed Schedule 45 50 55 60 65 70 75 80 85 90 95 2600 2700 2800 2900 3000 3100 3200 3300 3400 3500 Landing Weight lb Speed KIAS Stall Speed Speed at Touchdown Speed at 50 ft obstacle VREF for Short Field Landing Speed at 50 ft obstacle VREF for Normal Landing Maximum Landing Weight 342...

Страница 156: ... altitude of 4000 and 8000 feet is 1 7 and 3 4 gallons respectively The difference between these two altitudes yields 1 7 gallons No adjustment for non standard temperature is possible 4 What distance over the ground is covered in the climb under no wind conditions What is the approximate time 6 NM 2 9 Minutes Using the technique described in No 3 subtract the 4000 pressure altitude distance time ...

Страница 157: ...ng the A4 Flowmeter with cannulas or masks A4 FLOWMETER WITH CANNULA OR MASKS Oxygen System Usage Duration A4 FlowMeter STD Cannula 99 Confidence Tolerance 42 Cu Ft Serviced to 1 800 PSIG 10 12 14 16 18 20 22 24 0 0 0 1 0 0 2 0 0 3 0 0 4 0 0 5 0 0 6 0 0 7 0 0 8 0 0 9 0 0 1 0 0 0 1 1 0 0 1 2 0 0 1 3 0 0 1 4 0 0 1 5 0 0 Hours of Available O2 Usage Altitude Ft 1 000 1 PERSON 2 PERSONS 3 PERSONS 4 PER...

Страница 158: ...Section 5 Performance Columbia 400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 5 36 Latest Revision Level Date 11 10 2004 This Page Intentionally Left Blank ...

Страница 159: ...mination 6 8 Changes in the Airplane s Configuration 6 9 Determining Location FS of Installed Equipment in Relation to Datum 6 9 Weight and Balance Forms 6 9 Updating the Form 6 9 PROCEDURES FOR DETERMINING GROSS WEIGHT AND LOADED CG Useful Load and Stations 6 10 Baggage 6 10 Baggage Configuration Table 6 11 Baggage Nets 6 11 Summary of Loading Stations 6 12 Computing the Loaded Center of Gravity ...

Страница 160: ... Chapter Numbers 6 A1 Flight Operations Requirements 6 A1 Headsets 6 A1 EQUIPMENT FOR TYPES OF OPERATION LIST APPENDIX A 6 A1 Chapters 21 24 6 A1 Chapter 25 6 A2 Chapters 26 31 6 A3 Chapter 32 6 A4 Chapter 33 6 A4 Chapter 34 6 A4 Chapter 35 6 A6 Chapters 52 77 6 A7 INSTALLED EQUIPMENT LIST IEL APPENDIX B 6 B1 TABULATED AFTER MARKET EQUIPMENT LIST TAMEL Follows IEL WEIGHT BALANCE RECORD Follows TAM...

Страница 161: ...cedures for determining the weight and balance for each flight This part details specific procedures for airplane loading how loading affects the center of gravity plus a number of charts and graphs for determining the loaded center of gravity For pilot purposes in the Lancair Columbia 400 LC41 550FG the zero datum point is one inch aft of the tip of the propeller spinner All measurements from thi...

Страница 162: ...EVELING Because there are no perfectly level reference areas on the airplane and the use of Smart Levels is not common the airplane is leveled by use of a plumb bob suspended over a fixed reference point under the rear seats Moreover since the use of jacks with load cells is not prevalent the wheel scales method is described in this manual The following steps specify the procedures for installing ...

Страница 163: ... the brakes USING THE PERMANENT REFERENCE POINT 1 To determine the empty weight center of gravity of the airplane it is more convenient to work with the permanent reference The permanent reference point on the airplane is located at the forward part of the wing bottom in the center of the wing saddle and is 97 05 inches aft of the datum The location is shown in Figure 6 2 There is a pronounced sea...

Страница 164: ...he tires snapping a chalk line between these two points or laying a 7 3 foot board between the points Figure 6 4 MEASUREMENTS Measure the distance along the longitudinal axis from the permanent reference point tip of the plumb bob to the lateral reference line between the main gear tires This is Measurement A in MAIN GEAR TIRES CHALK MARKS NOSE GEAR TIRE FUSELAGE STATION 97 05 LOCATION OF PLUMB BO...

Страница 165: ...e 6 7 Operation No 1 Operation No 2 Operation No 3 Operation No 4 Operation No 5 Scale Location Weight Reading lbs Tare or Scale Error Corrected Weight lbs X Arm Inches Moments lbs inches Right Main Gear Right Scale Reading Scale Error Right Scale Wt Error X Main Gear Arm Right Gear Moments Left Main Gear Left Scale Reading Scale Error Left Scale Wt Error X Main Gear Arm Left Gear Moments Nose Gea...

Страница 166: ...Main Gear 991 pounds c Nose Gear 502 pounds 2 Scale Error Tare a Right Main Gear Scale is 1 pounds b Left Main Gear Scale is 2 pound c Nose Gear Scale is 3 pounds 3 Measurements a Measurement Distance A is 24 05 inches b Measurement Distance B is 56 15 inches c These uncorrected scale weights and tares are shown in Figure 6 8 Note that after correcting for scale error the right left and nose gear ...

Страница 167: ...stalled Equipment in Relation to the Datum If equipment is installed in the airplane the weight and balance information must be updated Individuals and companies who are involved with equipment installations and or modifications are generally competent and conversant with weight and balance issues These individuals or companies must be aware that the fixed reference point is located at fuselage st...

Страница 168: ...tation For example if weight is added at station 110 this means the added weight is 110 inches from the datum or zero reference point The drawing below Figure 6 10 shows the location of passenger and baggage loading stations The fuel is loaded at station 118 and is not shown in the figure These loading stations are summarized in Figure 6 12 Figure 6 10 BAGGAGE The space between the rear seat and t...

Страница 169: ...ced near the floor regardless of loading area and never load the baggage compartment to a level higher than the top of the hat rack If only Zone A is utilized the computations are based on an arm of 155 7 inches If both Zones A and B are utilized with defined weights in each area as shown in Configuration No 2 in Figure 6 11 two computations will be made to determine the total baggage weight and m...

Страница 170: ...9 8 inches 20 Lbs Usable Fuel The 8 gallons of unusable fuel is included in the empty weight The maximum total allowed baggage weight is 120 lbs and only 20 lbs of this total allowable weight can be placed on the rear baggage shelf The weight of items placed on the rear shelf must be subtracted from 120 lbs of total allowable baggage weight Figure 6 12 COMPUTING THE LOADED CENTER OF GRAVITY CG All...

Страница 171: ...buted over the main baggage area NOTE The basic empty weight used in this example will vary for each airplane Refer to the Weight and Balance Record which follows Appendix A of this section Figure 6 13 GRAPHICAL METHOD The multiplying graphs which begin on page 6 16 can be used to determine the moments for each weight location The answer is not as accurate as doing the calculation with a calculato...

Страница 172: ...deration is then made for distribution of the weight The objective in dealing with the balance limitation is to ensure that the center of gravity is within prescribed ranges at the specified gross weight The center of gravity range is referred to as the envelope The center of gravity envelope graph on page 6 18 shows the envelope for the Columbia 400 LC41 550FG Using data from the sample problem i...

Страница 173: ...HT The maximum empty weight of the Columbia 400 LC41 550FG is 2748 pounds The FAA requires the determination of this weight for FAA certification For airplanes certified in the IFR utility category a passenger weight of 190 pounds for each seat plus the fuel weight for 45 minutes of flight are used for this computation This equates to 92 pounds of fuel and 760 pounds of passenger weight for a tota...

Страница 174: ...test Revision Level Date 11 10 2004 Figure 6 16 Figure 6 17 Front Seat Moment Computations 0 10000 20000 30000 40000 50000 100 150 200 250 300 350 400 Weight lbs Moments lbs in Rear Seat Moment Computations 0 10000 20000 30000 40000 50000 60000 0 50 100 150 200 250 300 350 400 450 Weight lbs Moments lbs in ...

Страница 175: ... Figure 6 18 Figure 6 19 Fuel Moment Computations 0 10000 20000 30000 40000 50000 60000 70000 80000 100 150 200 250 300 350 400 450 500 550 600 Weight lbs Moments lbs in 40 Gals 60 Gals 80 Gals Baggage Moment Computations 0 5000 10000 15000 20000 25000 0 25 50 75 100 Weight lbs Moments lbs in Main Baggage Zone A Baggage Zone B Baggage Shelf ...

Страница 176: ...8 109 110 111 112 113 114 CG FS INCH WEIGHT LBS Max Landing Weight Max Zero Fuel Weight Figure 6 20 1 Airplane basic empty weight must be below Maximum Empty Weight M E W and above Minimum Flight Weight M F W 2 Weight must be below Maximum Landing Weight M L W for landing If overweight landing occurs see maintenance manual for required inspection prior to further flight 3 Weight and Center of Grav...

Страница 177: ...ight Operation Requirements identifies which equipment must be installed and functioning for the various flight conditions Headsets Use of the communications equipment requires a headset with a boom mike Headsets are optional items and not provided by the manufacturer since personal preference is a significant issue The pilot should add the actual weight of the headset to his or her weight and whe...

Страница 178: ...ck Rudder 1 23 04 LB53312000 B GMA 340 Audio Panel 23 05 LB53312000 B FN 200 Avionics Fan 24 01 LB71844000 B Belt driven Alternator 60 Amp 14 Volt 24 02 LB71845000 B Gear driven Alternator 60 Amp 14 Volt 24 03 LC71510000 B Batteries 14 Volt 15 Amp hour Lead acid 2 24 04 LB53243000 B Voltage Regulators 2 24 05 LC53242000 B Ground Power Plug Relay 24 06 LC53516001 B Ground Power Plug Socket 24 07 LC...

Страница 179: ...int Restraint Each 25 15 LA53253200 B Rear Seat Passengers Three Point Restraint Each 25 16 LB53255000 B Baggage Tie Downs and Restraining Net See 1 See 1 25 17 RC050002 B POH and FAA AFM Stowed in Copilot s Seatback 25 18 LB53311403 B Aural Warning Switch 25 19 LB53344901 O Carbon Monoxide Detector CHAPTERS 26 31 26 01 LA53254800 B Fire Extinguisher Unit 26 02 LA53254800 B Fire Extinguisher Mount...

Страница 180: ...100 B Main Wheel Brake and Tire 6 00 6 6 Ply Side 32 02 LA53322101 LA53322105 B Main Gear Fairings Each 32 03 LA53322109 LA53322113 B Main Wheel Fairings Each 32 04 LA53321123 B Main Wheel Fairings Mounting Plate 2 Each 32 05 LC71324000 B Nose Strut Fairing 32 06 LC71324003 B Nose Wheel Fairing 32 07 LC71320000 B Nose Gear Assembly 32 08 LA71322000 B Nose Wheel Tire and Tube 5 00 5 10 Ply CHAPTER ...

Страница 181: ...00 B COMM 2 Antenna 34 07 LA53342000 B NAV Antenna 34 08 LB53344500 B Garmin GTX 327 Transponder Unit 34 09 LB53344500 O Garmin GTX 330 Transponder Unit 34 10 LA57317000 B Transponder Antenna 34 11 LB53340005 B Turn Coordinator 34 12 LB53220000 O S TEC 55X Autopilot Flight Guidance Computer 34 13 LB53220000 O Roll Servo 34 14 LB53220000 O Pitch Servo 34 15 LB53220000 O Pressure Transducer 34 16 LC...

Страница 182: ...se Flight Speed Brake 2000 System Wing Units Each 34 26 LB53345011 O Precise Flight Speed Brake 2000 System Computer 34 27 LC53311400 B Avidyne EX5000 FlightMax MFD 34 28 LC53311400 B Avidyne FlightMax PFD 34 29 LB53342207 B Magnetometer 34 30 LC53344807 B Data Acquisition Unit 34 31 LB53345100 O XM Weather Wx Receiver 34 32 LB53345107 O XM Weather Wx Antenna 34 33 LC53342605 O ORBCOMM Antenna 34 ...

Страница 183: ...B53350000 B Face Mask with microphone 1 See 6 See 6 See 6 See 6 35 6 LB53350000 B Face Mask Front Passenger 1 See 6 See 6 See 6 See 6 35 7 LB53350000 B Bottle 1 with manifold See 6 See 6 See 6 See 6 35 8 LB53350000 B Bottle 2 with manifold See 6 See 6 See 6 See 6 35 9 LB53350000 B Bottle 3 with manifold See 6 See 6 See 6 See 6 CHAPTERS 52 77 53 01 LA53325100 B Cabin Entry Steps Each 7 53 02 LC5360...

Страница 184: ...n 6 Appendix A APPENDIX A Equipment Types of Operations Columbia 400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 6 A8 Latest Revision Level Date 11 10 2004 This Page Intentionally Left Blank ...

Страница 185: ...71844000 Belt driven Alternator 60 amp 14 volt 12 0 22 6 24 02 LB71845000 Gear driven Alternator 60 amp 14 volt 12 8 28 0 24 03 LC71510000 Batteries 14 Volt 15 Amp hour Lead acid 2 Each 14 5 204 5 24 04 LB53243000 Voltage Regulator 2 Each 3 0 70 0 24 05 LC53242000 Ground Power Plug Relay 0 9 55 0 24 06 LC53516001 Ground Power Plug Socket 0 8 153 0 24 07 LC53516003 Ground Power Plug Wiring 3 9 104 ...

Страница 186: ...32 89 8 27 01 LA53271000 Pilot s Control Stick 1 59 91 4 27 02 LA53274001 Pilot s Rudder Pedals 2 Each 1 0 71 6 27 03 LA53272000 Copilot s Control Stick 1 59 91 4 27 04 LA53274001 Copilot s Rudder Pedals 2 Each 1 0 71 6 31 01 LA53310018 Flight Hour Meter 0 13 78 0 31 02 LA57314000 OAT Probe 0 03 79 0 32 01 LA53321100 Main Wheel Brake and Tire 6 00 6 6 Ply Side 18 4 122 1 32 02 LA53322101 LA5332210...

Страница 187: ... 5 34 11 LB53340005 Turn Coordinator 1 96 149 0 34 12 LB53220000 S TEC 55X Autopilot Flight Guidance Computer 2 8 75 0 34 13 LB53220000 Roll Servo 2 9 133 0 34 14 LB53220000 Pitch Servo 2 9 206 0 34 15 LB53220000 Pressure Transducer 0 2 75 0 34 16 LC53311400 Attitude Indicator 2 7 81 0 34 17 LC53311400 Airspeed Indicator 0 77 78 0 34 18 LC53311400 Altimeter 0 9 75 0 34 19 LB53255400 Magnetic Compa...

Страница 188: ...lay 0 56 76 0 35 3 LB53350000 Cabin Distribution Manifold Assembly 0 54 130 6 35 4 LB53350000 Face Mask Rear Passengers 2 0 23 140 0 35 5 LB53350000 Face Mask with Microphone 1 0 58 140 0 35 6 LB53350000 Face Mask Front Passenger 1 0 12 140 0 35 7 LB53350000 Bottle 1 Fwd with Manifold 7 2 111 0 35 8 LB53350000 Bottle 2 Center with Manifold 7 1 116 5 35 9 LB53350000 Bottle 3 Aft with Manifold 7 2 1...

Страница 189: ...e is included in this section as a convenience to provide consistency in presentation The page does not replace or amend any required documentation attendant with the after market installation and or modification TABULATED AFTER MARKET EQUIPMENT LIST TAMEL Lancair Columbia 400 Item No Serial Part No ATA Chapter Item Weight lbs Arm ins 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 ...

Страница 190: ...TABULATED AFTER MARKET EQUIPMENT LIST TAMEL Lancair Columbia 400 Item No Serial Part No ATA Chapter Item Weight lbs Arm ins 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 ...

Страница 191: ...R 1 Date Airplane Weighed May 21 1927 Initial WEIGHT MOMENT CHANGE WEIGHT ADDED Lbs N A DESCRIPTION OF ARTICLE OR MODIFICATION BASIC AIRPLANE AS DELIVERED OUT N A ITEM MOVED IN N A WEIGHT BALANCE RECORD Continuing History of Changes in Structure or Equipment Affecting Weight and Balance AIRPLANE MODEL COLUMBIA 400 LC41 550FG DATE MOVED ...

Страница 192: ...R 1 Date Airplane Weighed May 21 1927 Initial WEIGHT MOMENT CHANGE WEIGHT ADDED Lbs DESCRIPTION OF ARTICLE OR MODIFICATION OUT ITEM MOVED IN WEIGHT BALANCE RECORD Continuing History of Changes in Structure or Equipment Affecting Weight and Balance AIRPLANE MODEL COLUMBIA 400 LC41 550FG DATE MOVED ...

Страница 193: ...9 Flight Control System Diagram 7 9 Control Lock 7 10 Trim System 7 10 Elevator and Aileron 7 10 Trim System Diagram 7 10 Hat Switches 7 10 Simultaneous Trim Application 7 11 Trim Position Indicator 7 11 Trim On Off Switch 7 11 Rudder Trim 7 11 Instrument Panel and Basic Cockpit Layout Diagram 7 12 Wing Flaps 7 13 Landing Gear 7 13 Main Gear 7 13 Nose Gear 7 13 Seats 7 14 Front Seat General 7 14 F...

Страница 194: ... 7 23 Fuel Quantity 7 23 Manifold Pressure 7 23 Fuel Flow 7 23 Dual Ammeter Loadmeter 7 23 Tachometer 7 24 Oil Temperature 7 24 Oil Pressure 7 24 Cylinder Head Temperature CHT 7 24 Turbine Inlet Temperature TIT 7 25 Flight Instrument Panel 7 25 Annunciator Panel 7 25 Aural Warning 7 26 Magnetic Compass 7 27 Remote Marker Beacon Repeater Indicator 7 27 Airspeed Indicator 7 28 Attitude Indicator 7 2...

Страница 195: ...ading 7 49 Hour Meter 7 50 Pitot Static System 7 50 ENGINE RELATED SYSTEMS 7 51 Fuel System 7 52 Fuel Quantity Indication 7 52 Fuel Selector 7 52 Fuel System Diagram 7 53 Fuel Low Annunciators 7 54 Fuel Vents 7 54 Fuel Drains and Strainer 7 54 Backup Boost Pump Vapor Suppression and Primer 7 54 Primer 7 54 Fuel Injection System 7 55 Environmental Control System ECS 7 55 Airflow 7 55 Floor Vent Sys...

Страница 196: ...i and Landing Lights 7 64 Stall Warning System 7 64 Stall Warning 7 64 Stall Warning System Electrical 7 65 Ground Power Plug 7 65 STANDARD AVIONICS INSTALLATION 7 66 Avidyne FlightMax EX5000 Multi Function Display 7 66 Introduction 7 66 General Overview 7 66 Operational Controls 7 67 Map Page Controls 7 69 Map Page Symbology 7 71 Map Orientation Control 7 73 Traffic Mode 7 74 Traffic 7 76 Trip Pa...

Страница 197: ...al 7 123 Subscription Updates 7 124 Abnormal Procedures 7 124 Normal Operations 7 125 Nav Com Bypass Switch 7 126 Garmin GTX 327 Transponder 7 126 General 7 126 Mode Selection Keys 7 126 Code Selection Keys 7 127 Keys for Other GTX 327 Functions 7 127 Function Displays 7 128 Configuration Mode 7 128 Altitude Trend Indicator 7 128 Timer Operation 7 128 Garmin GTX 330 Mode S Transponder 7 129 Genera...

Страница 198: ...ntrols 7 138 Oxygen Display 7 138 Oxygen Annunciator 7 139 Breathing Devices Masks and Cannulas 7 140 Flowmeter 7 140 Filler Port 7 141 OPTIONAL EQUIPMENT 7 142 S TEC System Fifty Five X Autopilot 7 142 System Overview 7 142 System Fifty five X Autopilot Pilot s Operating Handbook 7 142 Autopilot Disconnect Switch ADS 7 142 Autopilot Master Switch AMS 7 143 GPS VOR Interface 7 143 Precise Flight S...

Страница 199: ...ght control system wing flap system fuel system braking system heating and ventilating system door sealing system pitot pressure system static pressure system and the stall warning system In addition various non system components are described These include doors and exits baggage compartment seats seat belts and shoulder harnesses and the instrument panel Terms that are not well known and not con...

Страница 200: ...es are joined Before the fuselage is assembled into one unit cables control actuating systems and conduits are added because of the ease in access To prevent damage to the leading edge of the vertical stabilizer anti erosion tape may be installed Wings and Fuel Tanks The bottom of the wing is one continuous piece The spars are placed in the bottom wing and bonded to the bottom inside surface Next ...

Страница 201: ...on servo tab on the trailing edge of the left aileron assists in movement of the aileron The servo tab is connected to the aileron in a manner that causes the tab to move in a direction opposite the movement of the aileron The increased aerodynamic force applied to the tab helps to move the aileron and reduces the level of required force applied to the control stick Rudder The rudder is of one pie...

Страница 202: ...on the trim panel located to the right of the rocker switch panel The trim servos are protected by one amp circuit breakers See Figure 7 2 for an illustration of the trim system TRIM SYSTEM DIAGRAM Figure 7 2 The trim surfaces are moved by push rods connected between each tab and a servomotor The aileron tab has one actuating rod and the elevator tab has two The second actuating rod on the elevato...

Страница 203: ...nge of travel If the two green LED s in the middle of the is lit and no blue lights are illuminated both tabs are in the approximate neutral position The LED s level of brightness is controlled by the position lights switch When the position lights are on the trim lights are in the dim mode and when the position lights are off the trim lights are in the bright mode Trim On Off Reset Switch The tri...

Страница 204: ...witch 18 Attitude Indicator 19 Airspeed Indicator 7 Left dimmer controls backlighting for radios and switches right dimmer controls engine and flight instrument backlighting 20 Altimeter 7 1 Alternate Static Air 21 Entegra Multi function Display 7 2 Heated Induction Air 22 Lower Instrument Panel 8 Rocker Switch Panel 23 Environmental Control System ECS Panel 9 Master Switch Panel 24 Flap Panel Fla...

Страница 205: ...nd testing of the lights is discussed later in this section on page 7 64 See Figure 7 3 for a drawing of the instrument panel and cockpit layout When the flaps are in the up position the knob is in a position parallel to the floor and points to the UP label on the panel overlay When flaps are in the takeoff position the knob is rotated 30 counterclockwise from UP and pointed to the T O label When ...

Страница 206: ...nt seats are adjustable fore and aft through a range of approximately seven inches The adjustment control for the seats is located below the seat cushion on the left side To adjust the position of either seat move the control lever towards the middle until the seat unlocks from the seat track and adjust the seat to the desired position Release the adjustment control when the seat is in the desired...

Страница 207: ... and restrict use of the latching mechanism The aircraft should never be taxied while the doors are in the full up position The doors may be opened 6 to 8 inches during taxi which can be controlled by grasping the armrest or use of the door strap Latching Mechanism From the exterior the latching mechanism on each cabin door is operated through movement of the exterior door handle The handle is mou...

Страница 208: ...stem to operate The cabin door latching mechanism also controls the dump door seal valve When either cabin door latching mechanism is moved more than a half inch towards the open position the dump valve is engaged and the pressure in the seals is dumped This prevents inadvertent operation of the doors when they are sealed however setting the door seal switch to the off position after landing is re...

Страница 209: ...Depressing the top portion of the rudder pedals translates this pressure into hydraulic pressure This pressure is transmitted through a series of hard aluminum and steel grade Teflon lines to pistons in the brake housing of each brake The piston activates the brake calipers that apply friction to the chrome steel discs Each disc is connected to a wheel on the main landing gear and when the caliper...

Страница 210: ...he same direction As is the case with most light aircraft turning requires a certain amount of forward momentum Once the airplane is moving forward applying right or left brake will cause the airplane to steer in the same direction There are two important considerations First use enough power so that forward momentum is maintained otherwise the differential braking will stop the airplane Second av...

Страница 211: ...tion from too much pressure ENGINE CONTROLS Throttle The throttle controls the volume of air that enters the cylinders The control has a black circular knob and is located to the right of the rocker switch panel and above the radios The throttle has a friction control collar that increases or decreases the pressure required to advance or retard the control It is used to lock the throttle at a part...

Страница 212: ...aded constant speed propeller with a McCauley governor In a constant speed propeller system the angle of the propeller blade changes automatically to maintain the selected RPM For this to happen the angle of the propeller blade must change as power air density or airspeed changes A decrease in blade angle decreases the air loads on the propeller while an increase in blade angle increases air loads...

Страница 213: ...logged alternate induction air can be used any time If the filter is clogged and alternate induction air is selected the engine is drawing hot air into the induction system This increases the chance for engine detonation To limit the chance for engine detonation set the mixture to full rich and do not use more than 85 power if the outside air temperature is greater than 32 F Cooling The airplane h...

Страница 214: ...through transfer tubes and drain holes where it is returned to the oil sump If the filter becomes clogged and prevents oil from moving through the system a bypass valve reroutes the oil around the filter In this event the lubricating oil is of course unfiltered However rerouting the oil will prevent engine failure It is important to note that the pilot will have no indication that the oil filter h...

Страница 215: ...ights is discussed later in this section on page 7 64 The pilot is reminded that the fuel gauges are approximate indications and are never substitutes for proper planning and pilot technique Manifold Pressure The manifold pressure gauge is in the engine instrument panel in the top right position The instrument is a dual presentation gauge with manifold pressure indications on the left and fuel flo...

Страница 216: ... oil temperature in degrees Fahrenheit F in 20 F increments The normal operating limits Green Arc displayed on the gauge range from 170 F to 220 F with a red radial upper limit of 240 F The thermal bulb which is the source point for measurement of oil temperature is located near the oil cooler Power for the temperature gauge is supplied by the airplane s electrical system and the oil temperature g...

Страница 217: ...7 12 Annunciator Panel The presentation of the annunciator panel is shown in Figure 7 5 The number below each label identifies the page number that contains the relative discussion Controlling light intensity and testing these lights is discussed in this section on page 7 64 1 If the DOOR OPEN light is on one or more of the airplane s doors is not properly secured 2 If the FUEL VALVE light is on t...

Страница 218: ...provide a reminder when the Count Down timer reaches zero The aural warning system operates when the avionics master is on and there is engine oil pressure This feature prevents the warning system from going through all the commands when power is first applied There is also a two second delay to allow fuel tank selection without a nuisance warning An acknowledge button is located below the annunci...

Страница 219: ... failure 3 Fuel Valve this warning is activated when the fuel valve is not in the left or right tank detents 4 Fuel Pump On this warning is activated when the fuel pressure is less than 5 5 psi 5 Traffic With TCAD installed This warning phrase is always preceded by a tone and then begins as Traffic The clock position relative altitude and range of the intruder is then announced Refer to Audible Ad...

Страница 220: ...uses the pressure altitude scale in a window at the top of the instrument to move under a stationary temperature scale Rotate the knob until the pressure altitude in increments of 1000 feet is opposite the temperature C in increments of 10 and read the TAS on the true airspeed ring Greater accuracy is produced if calibrated airspeed is used rather than indicated airspeed Attitude Indicator The bac...

Страница 221: ...ne indexed in increments of 5 with a label at the 10 and 20º points Altimeter The backup altimeter is part of the pitot static system which is discussed on page 7 50 The instrument measures the height above sea level and is correctable for variations in local pressure The pressure source for the instrument is from the static air vent An aneroid or diaphragm within the instrument either expands or ...

Страница 222: ...ghtMax Entegra Primary Flight Display Pilot s Guide is included as part of the delivery kit with the airplane and is the primary source document for operation of the airplane s PFD as well as how it is integrated with other standard and optional systems Proper use of all the PFD features requires some practice and study However the long term benefits more than justify the time devoted to learning ...

Страница 223: ...orizon when above 50 and below 30 90 is represented by small circles Bank Angle Indicator Composed of an inverted white triangle and an upright white triangular Roll Pointer The upright white triangle points to the current bank angle Graduations are at 0 10 20 30 45 and 60 degrees Note the 0 and 45 degree marks are inverted triangles Skid Slip Indicator The black trapezoid is centered under the ro...

Страница 224: ...ation Indicator CDI The green single line CDI displays deviation from the set or desired course Bearing Pointer The blue dual line bearing pointer is associated with the Bearing source and displays the current bearing to the Bearing waypoint GPS1 or GPS2 or bearing to the station VLOC1 or VLOC2 A bearing pointer will not be displayed if the VLOC source is tuned to an ILS or LOC station Compass Ros...

Страница 225: ...ug Controlled by the right knob when the Alt Bug button is selected The notched part of the magenta bug symbol indicates the current altitude preselect value When the selected value is outside the current altimeter field of view the bug is positioned at the appropriate end of the tape and remains in partial view The bug is solid when coupled to the autopilot and hollow when not coupled Altitude Pr...

Страница 226: ... and VLOC2 The content of the associated data block varies according to the selected source as follows NAV Source Data Block Format GPS1 or GPS2 Waypoint Identifier Desired Track to Waypoint Distance to Waypoint Time to Go to Waypoint VLOC1 or VLOC2 VOR Tuned VOR VOR Frequency Course VLOC1 or VLOC2 ILS or LOC Tuned ILS or LOC Localizer Frequency Course Bearing Navigation The adjacent push button c...

Страница 227: ...ce to Waypoint Time to Go to Waypoint VLOC1 or VLOC2 VOR Tuned VOR VOR Frequency Bearing to station VLOC1 or VLOC2 ILS or LOC Tuned ILS or LOC Localizer Frequency OFF Blank NOTE The Bearing Aux and Range View button selections will all timeout back to Nav button selection ten seconds after they were last pushed or changed by knob rotation Because of the button timeouts a recommended technique is t...

Страница 228: ...Air Speed Air Speed Tape A C Ref Symbol CDI Flt Dir Command Bars A P Annunciation Window Pitch Ladder Bank Angle Indicator Skid Slip Indicator Altitude Preselect Glideslope Indicator Vertical Speed Indicator Altitude Window Vertical Speed Bug Vertical Speed Needle Altitude Bug Kollsman Window Magnetic Heading Moving Map Wind Vector Map Range Projected Track Dashed Lined CDI Bearing Pointer Heading...

Страница 229: ...atic once power is applied via the battery switch Engine start will not affect the ADAHRS alignment A common Entegra PFD startup procedure is to turn on the battery and conduct the aircraft preflight during the ADAHRS alignment process The PFD presents the initialization display immediately after power is applied The software version number and the aircraft the speeds are configured for are listed...

Страница 230: ...D in two of the four possible view selections full compass rose with map arc view with map GPS NAV 1 is also the primary source for groundspeed readout and a required element for the wind vector calculation and display In the event GPS NAV 1 is unavailable groundspeed and wind vector data are derived from GPS NAV 2 If the Nav source is selected to a VOR or localizer source the HSI will display the...

Страница 231: ...CDI button on the GPS NAV is toggled from GPS to VLOC and back the Nav source of the Entegra PFD will change to follow A recommended technique is to use the CDI button on GPS NAV 1 to toggle the Nav source back and forth The CDI button on the GPS NAV 1 makes it easy to switch the PFD between GPS 1 and VLOC 1 and back Precision Flight with PFD This section describes several techniques which take ad...

Страница 232: ...icators The trend indicators display the aircraft s projected airspeed and altitude six seconds in the future To capture and maintain a desired airspeed or altitude adjust pitch and or power to align the trend indicator with the desired airspeed or altitude This will result in a smooth capture of the desired airspeed and altitude See Figure 7 9 1 Airspeed Trend Indicator The tip of the blue airspe...

Страница 233: ...essive Pitch Chevrons The large white chevrons are displayed at pitch values greater than 50 and less than 30 In all cases the chevrons point towards the horizon line Figure 7 9 Autopilot Use and Control The Entegra PFD is fully integrated with the S TEC System Fifty Five X autopilot The Heading Altitude and VSI reference bugs are provided on the Entegra PFD to aid in pilot situational awareness a...

Страница 234: ...ot will track the new heading bug value 2 Nav Apr Mode Press the NAV button on the autopilot control head to engage Nav mode The autopilot will intercept and track the desired course In this mode the autopilot tracks the active plan of the selected GPS NAV Nav GPS1 or GPS2 or an active VOR or localizer Nav VLOC1 or VLOC2 The autopilot control head and the PFD will indicate NAV If a localizer is se...

Страница 235: ...peed Mode Push the VSI Bug button and rotate the PFD knob to set the desired vertical speed The VSI bug is hollow at this point Engage the VS mode by pressing the VS button on the autopilot control head At this point the VSI bug will become solid magenta The flight director steering command bars will be present when the aircraft is setup to display the flight director When VS mode is cancelled the...

Страница 236: ...e available Alt Hold mode and VS mode are still available and may be controlled using the Alt and VS buttons and the rotary knob on the autopilot control head See the autopilot user s guide for usage instructions CAUTION When engaging the altitude capture mode confirm that both ALT and VS are engaged on the autopilot If VS is not engaged the autopilot will level the aircraft at the current altitud...

Страница 237: ...S NAV system has been setup to Autoslew The CDI deflection will be driven by the localizer signal itself regardless of the course setting To perform an autopilot coupled approach ensure the approach has been activated in the GPS selected as the Nav source At that point press the NAV button on the autopilot control head to activate Nav mode Press the APR button on the Autopilot control head to acti...

Страница 238: ...be set to reverse REV mode Consult the autopilot POH for proper orientation Missed Approach Prior to missed approach disconnect the autopilot ensure the aircraft is trimmed for the power setting establish a climb attitude and use Entegra s Alt Bug to set the desired missed altitude On the climb out select HDG or NAV depending on missed approach instructions on the autopilot press ALT and VS simult...

Страница 239: ...r ground track and flight plan Crosscheck Monitor The Entegra PFD comes equipped with a self check monitor When the self check monitor detects a condition that does not warrant removal of data a directive warning message is displayed to the pilot to CROSSCHECK ATTITUDE see Figure 7 12 1 When this message is displayed the pilot should scan all backup instruments and auxiliary instruments attitude i...

Страница 240: ... Attitude data will be removed from the display and replaced with a red X and 2 An Attitude Fail Refer to backup gauges message will be displayed and NOTE Use the backup instruments and or outside visual references to obtain straight and level conditions 3 A Fast Erect button label and message will be displayed 4 When the Fast Erect button is pressed the message will change to Maintain straight an...

Страница 241: ... data are unavailable 1 Attitude data will be removed from the display see Figure 7 14 2 An Attitude Fail Refer to Backup Gauges message will be displayed 3 Wind vector data will be removed from the display 4 Heading data will be removed from the display and 5 HSI navigation data will be removed from the display NOTE Use back up instruments for attitude and heading for the remainder of the flight ...

Страница 242: ...when the airplane is secured on the ground during extremely high wind conditions The hour meter will run even if the master switches are turned off during flight operations The hour meter is provided to record time in service which is the basis for routine maintenance maintenance inspections and the time between overhaul TBO on the engine and other airplane components PITOT STATIC SYSTEM The pitot...

Страница 243: ... position Water accumulation in the static line reservoirs is a possibility and certain precautions should be taken to prevent excessive accumulation Normal accumulation is anticipated in the system which is why a reservoir is incorporated The reservoir is designed to collect this accumulation but excessive accumulation can result in errors to the instruments and equipment connected with the pitot...

Страница 244: ... levels in each compartment and requires two floats in each tank to accurately measure total quantity The floats move up and down on a pivot point between the top and bottom of the compartment and the position of each float is summed into a single indication for the left and right tanks The positions of the floats depend on the fuel level changes in the float position increases or decreases resist...

Страница 245: ... position to the left or right tank pull up on selector and rotate the handle to the desired tank FILLER CAP VAPOR SUPPRESS SWITCH BACKUP BOOST ARM THROTTLE FUEL VENT FUEL VENT FILLER CAP LOW FUEL ANNUNCIATOR SWITCHES FUEL DRAIN FUEL DRAIN SLOSH BOXES AUX FUEL PUMP FUEL STRAINER ENG FUEL PUMP THROTTLE AND METERING UNIT MIXTURE CONTROL FUEL MANIFOLD FS TAMU TO INJECTOR NOZZLES MP FF MANIFOLD PRESS ...

Страница 246: ...inboard section of each tank contains a fuel drain near the lowest point in each tank The fuel drain can be opened intermittently for a small sample or it can be locked open to remove a large quantity of fuel The gascolator or fuel strainer is located under the fuselage on the left side near the wing saddle Open the accessory door in this area for access to the gascolator There is a conventional d...

Страница 247: ...r Vent System The floor vent system provides mixed air to vents under both knee bolsters in the front seat area and to an eyeball vent in the back lower portion of the front seat center storage console Rotating the vents clockwise and counterclockwise controls the airflow to the rear floor eyeball vents while the front vents have fixed rates The temperature and floor air control knobs control the ...

Страница 248: ...ion Level Date 11 10 2004 ENVIRONMENTAL CONTROL SYSTEM DIAGRAM AND PANEL Figure 7 16 FRONT SEAT EYEBALL VENT CONTROL PANEL OUTSIDE RAM AIR ECS VALVE AIR BLEED NOZZLE OFF INTERCOOLER FAN DEFROSTER FRONT SEAT EYEBALL VENT FRONT FLOOR VENT FRONT FLOOR VENT REAR EYEBALL FLOOR VENT COLD AIR HEATED AIR MIXED AIR REAR SEATING EYEBALL VENTS MANIFOLD ...

Страница 249: ...lectrical items on the left bus by connecting the left bus to the right bus As its name may suggest power to the essential bus is never affected provided power from at least one bus left or right is available The essential bus is diode fed i e current will only flow in one direction from both the right bus and the left bus allowing the essential equipment to have two sources of power A summary of ...

Страница 250: ...tch is a split rocker design with the alternator switch on the left side and the battery switch on the right side Pressing the top of the alternator portion of the split switch turns on both switches and pressing the bottom of the battery portion of the split switch turns off both switches The battery side of the switch is used on the ground for checking electrical devices and will limit battery d...

Страница 251: ...es Engine Instruments Carbon Monoxide Detector Oxygen Position Lights Landing Light Left Voltage Regulator Clock and Cabin Fan PFD Power 1 amp 10 amp 3 amp 3 amp 2 amp 3 amp 10 amp 4 amp 5 amp 7 5 amp 10 amp RIGHT BUS Strobe Lights Taxi Light Right Voltage Regulator Door Seal Power Point PFD Power Elevator Trim 10 amp 4 amp 5 amp 5 amp 10 amp 1 amp ESSENTIAL BUS Attitude Horizon Turn Coordinator P...

Страница 252: ...at turn on various lights and devices The labeling of each switch is shown in Figure 7 18 The number below each switch identifies the page number that contains the related discussion The top of each rocker switch is engraved with an Off placard which is only visible when the switch is turned off PITOT HEAT POSITION LIGHTS STROBE LIGHTS LANDING LIGHT TAXI LIGHT DOOR SEAL VAPOR SUPPRESS BACKUP PUMP ...

Страница 253: ...ND POWER PLUG LEFT BATTERY BUS RIGHT BATTERY BUS Hobbs Meter ELT Attitude Horizon Panel Lights Annunciators Left Bus Relays Fuel Pump Stall Warning Flaps Right Bus Relays Turn Coordinator Courtesy Light Taxi Light Elevator Trim Door Seal Power Point Right Voltage Regulator Strobe Lights Audio Voice GPS 2 Nav Com 1 Com 2 GPS 1 Traffic Weather MFD Autopilot Xponder Enc Fan Carbon Monoxide Detector P...

Страница 254: ...ors are closed This design has two advantageous features First opening either of the main cabin doors provides an immediate light source for preflight operations passenger access and baggage loading Second the flip lights when rotated either left or right serve as emergency lighting in situations which necessitate turning off the master switch The only disadvantage is that the flip lights can inad...

Страница 255: ...ctivates timer that turns off access lights after 10 minutes Operates with master switch on or off Overhead Swivel Lights Two overhead swivel lights in the front seat area One centered swivel light in the rear seat area The left thumb wheel dimmer switch is in the overhead panel Individual switch at each light Master switch must be on for the system to operate Glare Shield Flood Bar Color correct ...

Страница 256: ...e interest of safety to turn off the lights For example strobe lights shall be turned off on the ground if they adversely affect ground personnel or other pilots and in flight when there are adverse reflections from clouds The exterior lighting system includes the position lights the strobe or anti collision lights the landing light and the taxi lights These lights are activated through use of swi...

Страница 257: ...behind the left wing between the trailing edge of the flap and the step The plug allows connection to a 12 volt DC power source for maintenance and allows the engine to be started from a ground power cart The aircraft power must be off when the plug is connected or disconnected to the 12 volt DC power source Once connected turning the BATT switches on will charge the batteries CAUTION The battery ...

Страница 258: ... s Guide The MFD provides a pictorial view of your flight situation based on input from your GPS navigator It utilizes on board database information for mapping off route navigation data such as nearby airports VORs NDBs special use and restricted airspace etc as well as an extensive terrain interstate highways water and obstacle databases The controls on the bezel of the FlightMax EX5000 are plac...

Страница 259: ...7 Columbia 400 LC41 550FG Description of the Airplane and Systems Initial Issue of Manual November 10 2004 RC050002 Latest Revision Level Date A 12 01 2004 7 67 Operational Controls Figure 7 21 1 2 3 4 5 6 7 4 ...

Страница 260: ... the Trip Page Nearest Page TAWS Page when equipped Chart Page when equipped Checklist Pages when equipped Setup Pages and the Engine Page The current page is highlighted in the lower left corner of the screen 6 Range and Cursor Control Right knob controls the map s range When other pages are in view the right knob provides selection control 7 Message Bar The message bar is used to keep the pilot ...

Страница 261: ...l November 10 2004 RC050002 Latest Revision Level Date A 12 01 2004 7 69 Map Page Controls Line select keys on the left side of the bezel provide access to sensor modes Line select keys on the right side of the bezel access the mapping functions and control how the map is viewed Figure 7 22 1 2 3 ...

Страница 262: ... OFF The lightning sensor maps thunderstorm activity by monitoring electrical discharge activity within a 200 nm radius of the aircraft Lightning strikes less than 25 nm are not displayed if the display range is set to less than 25 nm If the display range is set to greater than 25 nm all lightning strikes will be displayed c Clear Strikes button removes lightning symbols to allow for the refresh o...

Страница 263: ...urrent range setting The range number is the distance from the airplane symbol to the compass arc 6 Terrain Scale Shows highest and lowest limits of terrain in displayed area Legend colors in between these numerics represent terrain elevations Blue obstacle clearance number shows the top of the highest obstacle when greater than the highest displayed terrain Terrain data is not displayed when your...

Страница 264: ...Traffic Indications Shows traffic symbol relative to current position and includes relative altitude when available with respect to airplane symbol See traffic sensor user s manual for further details When available TIS installations will show a ground track stinger for each intruder indicating the intruder s track as measured by ground radar 11 Lightning Indications Not currently installed Shows ...

Страница 265: ...he orientation of the map and sensor data displayed on the MFD with the Map View button MFD traffic and lightning symbols are positioned relative to the aircraft symbol nose When the Map View is North Up extra pilot effort may be needed to locate traffic outside the aircraft Set Map View to Center or Forward to display this data consistent with typical dedicated traffic and lightning sensor displa...

Страница 266: ...400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 7 74 Latest Revision Level Date A 12 01 2004 Traffic Mode When a Traffic Advisory TA is reported from the traffic sensor the MFD displays a traffic alert message in the Message Bar Figure 7 24 2 1 ...

Страница 267: ...ll be automatically removed when the threat is reduced or the intruder is no longer present 2 Exit Traffic button restores the Map page to the previous settings If the Map page is restored prior to acknowledging a TA the message will remain displayed and acknowledging it will once again bring up the dedicated traffic display NOTE Traffic information is provided to the pilot as an aid to visually a...

Страница 268: ...r track information is available the appropriate symbol will be shown with a stinger which depicts the current ground track of the intruder as detected by ATC radar systems It should be noted that the traffic sensor intruder track information is known to an accuracy within 45 of true intruder track This should be taken into account when visually acquiring the reported traffic Also note that intrud...

Страница 269: ...ap alignment i e if the MFD map is set for North Up the intruder is flying a track somewhere between 023 and 067 This is the accuracy limit of the intruder track data For TIS installations the following may be reported in the Traffic status block on the EX5000 Map page 1 OPER The TIS sensor is operating normally 2 CST 00 00 The TIS sensor has temporarily lost the information feed from ground based...

Страница 270: ... GPS The route legs advance with each waypoint message Turning the left knob one detent to the right brings up the Trip Page which shows the remaining legs in the current flight plan and other data being received by the MFD from the GPS If the flight plan doesn t fit on the screen an ellipse is shown in the next to last line The last line is still displayed All flight plans are from the GPS A No F...

Страница 271: ... h Nrst METAR Available with Datalink enabled Displays Graphical Metar and reporting point identifier NOTE When the MFD is interfaced to a Garmin GNS 430 via RS 232 the GPS may send duplicate waypoints while in approach mode These duplicate waypoints may affect the distance and time readings on the trip page Approach procedures should be flown using the GPS as the primary source of navigation info...

Страница 272: ...e better the signal strength You should normally see values between 4 and 10 c Message Quality Even when the signal strength is good messages may be dropped if the local interference level is too high You should see values between 7 and 10 during normal operation 7 Select Knob Moves the cursor over the desired waypoint in the flight plan which selects the plain English textual METAR to be displaye...

Страница 273: ...From the Trip page turning the left knob one detent to the right brings up the NRST page The Nearest page brings up the nearest airports within 100 nm of your present position Through the line select keys you will also have access to detailed information about each airport The line select keys also allow you to view the nearest VORs NDBs intersections and obstacles Figure 7 26 5 4 3 2 1 ...

Страница 274: ...lable If Broadcast datalink is installed the lower portion of the screen will display the text METAR for any airport displaying a graphical METAR symbol 2 Type Cycles through the various data types in the following order Airports Nearest Present Position Airports Neares Destination VORs NDBs Intersections Obstacles 3 Selection Control Use line select keys or right knob to move the cursor up or dow...

Страница 275: ...50002 Latest Revision Level Date A 12 01 2004 7 83 Checklist Normal Turning the left knob to Chklst on the page bar brings up the Checklist Page which provides a list of all the Normal Procedure checklists The MFD startup screen and the MFD setup page display the current checklist version that is loaded Figure 7 27 400 ...

Страница 276: ...g items a Once inside a Checklist the right knob can be used to move up and down the checklist The current step in the checklist is highlighted in magenta and has an arrow pointing to it from the right side b Pressing Done changes the current checklist item to green places a checkmark to the right of it and automatically steps down to the next checklist item c Pressing Back brings you back to the ...

Страница 277: ...Section 7 Columbia 400 LC41 550FG Description of the Airplane and Systems Initial Issue of Manual November 10 2004 RC050002 Latest Revision Level Date A 12 01 2004 7 85 Figure 7 28 400 a e d c b ...

Страница 278: ...al Issue of Manual November 10 2004 7 86 Latest Revision Level Date A 12 01 2004 Checklist Emergency The MFD includes complete Emergency checklists with one button access from any page being displayed by pressing the Emerg Checklist line select key in the lower left corner Figure 7 29 400 ...

Страница 279: ...hecklist Types Provides access to the top level Emergency checklists for each phase of flight including Ground Emergency In Flight Emergency Landing Emergency and System Malfunctions 3 Available Checklists Menu of checklists within each type Pushing the Show Checklist key takes you directly to the desired list 4 Selection Control Use right knob to move the blue outlined box up or down to highlight...

Страница 280: ...ink Text METARs also appear on both types of Nearest Airport pages Nearest to Position and Nearest to Destination 3 Graphical METARs Flag symbols which are color coded to summarize a recent surface weather observation Graphical METARs appear on the Map page Trip page and on both types of Nearest Airport pages They allow a big picture view of general weather conditions in an area The presence of a ...

Страница 281: ...where you are and that you are about to begin a flight Weather data will begin transferring to your airplane based upon your user preferences no action is required to begin receiving weather Note that the satellite receiver must have a clear view of the sky and generally will not work inside a hangar Upon entry of a flight plan or a direct to waypoint your MFD will automatically download the weath...

Страница 282: ...rning the Narrowcast system on or off If Narrowcast is disabled subsequent flights will not be shown on your account page at www myavidyne com If Broadcast datalink is also installed this setting is labeled Multilink Enabled 3 Save Press to save any changes made and return to the Aux page 4 Coverage Area Specifies the type of coverage being requested Current Position Requests weather information w...

Страница 283: ... d Faster request intervals will consume significantly more message units 8 Cancel Press to go back to the Main Setup menu without accepting any changes 9 SUA Status Allows enabling disabling of the reporting of the activity status of Special Use Airspace SUA included in the nav database and depicted on the Map page 10 TFR Status Allows enabling disabling of the reporting of Temporary Flight Restr...

Страница 284: ... single and triple thick The thick side of the line indicates the inside of the affected region The regions are labeled according to the type of Airmet Sigmet and the label is located in the interior of the depicted region The boundary of the available weather coverage area is shown by hash marks The intent of the datalink weather boundary is to clearly show when there is actual weather in the are...

Страница 285: ...her action is required on your part if necessary you will have to move your airplane out of the hangar so that the satellite receiver can see a satellite The Broadcast datalink receiver continuously receives all weather data for the entire contiguous United States CONUS It is not necessary to enable or disable the receipt of individual types of data The display of the received data is controlled o...

Страница 286: ... Lightning 4 Wx Rprts button controls the display of METAR symbols AIRMETs and SIGMETs on the Map page Pressing the button toggles through All METARS SIGMET AIRMET and Display Off 5 Lightning strike symbols Lightning information from the XM broadcast satellite is matched to grid coordinates with a resolution of approximately 2 NM Overlapping lightning symbols may be decluttered for clarity The lig...

Страница 287: ...th solid red lines on the Map page Note that at a full Map declutter setting all navigation data and airspace removed TFRs will also be removed from the display Without a Traffic sensor installed the MFD takes advantage of the available buttons and the WX Reports button is split into two buttons Air Sig and Metars as shown below Figure 7 31 Figure 7 31 shows the folloing items 1 The Air Sig button...

Страница 288: ...dcast weather datalink includes the continental United States Outside this area weather information is not provided The boundary of the coverage area is shown on the Map page as a hatched pattern as seen in this excerpt near the Canadian border see Figure 7 32 Some remote areas of the United States may not have NEXRAD coverage See the Aeronautical Information Manual AIM for more information on NEX...

Страница 289: ...flightplan exceed 100 miles in length the MFD will select intermediate waypoints in between the waypoints of the leg in order to provide greater situational awareness of the weather conditions along the route Figure 7 33 Figure 7 33 shows the following items 1 METAR symbols Using the same METAR condition symbols as the Map page a METAR report is shown for each flightplan waypoint 2 METAR text the ...

Страница 290: ... the Broadcast satellite receiver Note that your Service Level may be reported as None defined like the example above if your weather data subscription has only recently been activated Once the datalink receiver has confirmed your Service Level it will be displayed here for instance Aviator or Aviator Pro This process may take a day or two to be triggered depending on your MFD usage but you will s...

Страница 291: ...side of CONUS See page 73 for a description of the Narrowcast service area c Datalink Messaging The unique 2 way Narrowcast system provides simple text messaging between the cockpit and a password protected page on www myavidyne com You control access to this page by creating a password which you give to anyone with whom you want to exchange messages during flight d Flight Tracking Regular automat...

Страница 292: ...sing Multilink for Backup When Multilink is enabled the MFD checks the status of the Broadcast system at power up and every 10 minutes thereafter NOTE If the Broadcast system becomes unusable or unavailable the types lf weather data enabled on the Datalink Setup page will automatically be sent via the Narrowcast system 5 Using Multilink for Expanded Coverage When Multilink is enabled the MFD sends...

Страница 293: ...rea of Broadcast Datalink The first illustration below shows the Map page seen on a Broadcast Datalink only unit for this flight and the next illustration below shows the same page on a Multilinkenabled unit with the Narrowcast NEXRAD overlay selected Note the difference in the hatched area of both images which clearly shows the expanded coverage area of Narrowcast In this case some very significa...

Страница 294: ...anual selection is necessary With Multilink enabled Canadian METAR data obtained via Narrowcast is simply added to the MFD s available pool of data and is displayed along with Broadcast data As an example consider a flight from Watertown NY to Pellston MI Again this route is largely over Canada While Broadcast NEXRAD covers this route fairly well there are no Canadian METAR reports received via th...

Страница 295: ...th data already received via the Broadcast system Since weather data will be transmitted whenever the selected Coverage Area extends outside of CONUS it is a good idea to be sure that your Coverage Area is selected appropriately For example consider a flight from Norfolk VA to Frederick MD If the Coverage Area settings are Flight Plan and 400 nm with all weather types selected the Multilink system...

Страница 296: ...u plan to use Multilink mainly as an active backup for Broadcast consider setting the coverage area to Current Position and 200 nm or even 100 nm if you regularly fly in the northeastern United States Remember that in the Boston area a setting of 200 nm puts the Coverage Area outside of CONUS and will cause the NOC to send Narrowcast data for every flight c Datalink Messaging Flight Tracking Only ...

Страница 297: ...ormal operating conditions Caution Zone readings will cause the appropriate annunciation to turn yellow while Warning Zone readings will cause a red indication Figure 7 34 shows the following items 1 Gauges a Manifold Pressure Displays current engine power in inches of Hg as measured at the engine s induction system and reported by the DAU b RPM Displays current engine speed in revolutions per min...

Страница 298: ...Section 7 Description of the Airplane and Systems Columbia 400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 7 106 Latest Revision Level Date A 12 01 2004 Figure 7 34 5 4 3 2 1 ...

Страница 299: ...ed on the fuel flow as reported by the DAU and the ground speed as reported by the GPS This value is only reported if the GPS ground speed is greater than 50 knots 5 Engine Page Cylinder Temperatures a Turbine Inlet Temperature TIT Indicates the exhaust temperature at the left turbocharger intake in degrees Fahrenheit NOTE The TIT displayed on the MFD may indicate up to 50 F higher than the analog...

Страница 300: ... 36 Engine Instruments Lean Assist The MFD is equipped with a lean assist function which is used to set the optimum mixture for various operating conditions using TIT values Above 85 power operations must take place at full rich leaning is not allowed Leaning for Best Power Between 65 and 85 power leaning is only allowed to the best power point which is rich of the peak TIT See Figure 7 37 ...

Страница 301: ... map page Figure 7 37 After following the instructions above the mixture setting is just below peak TIT on the rich side If the mixture is moved too far towards rich the MFD will annunciate Rich of Best Power and if moved too far lean Too Lean Richen Mixture Also as a precaution the Lean Assist algorithm will not allow leaning past a TIT of 1700 F If there is no peak detected before reaching 1700 ...

Страница 302: ... to exit the Lean Assist function The lean state in this case Economy will continue to be provided in the data block on the map page Figure 7 38 If the mixture is leaned too far past the Best Economy point the MFD will annunciate Too Lean If the mixture is richened back towards the TIT peak the MFD will switch to power mode and instruct the pilot to richen for best power As a precaution the Lean A...

Страница 303: ...a fuel flow adjustment 4 Pwr Change When the lean state is changed by a power adjustment Figure 7 39 Engine Instruments Graphical Data Blocks on Map Page The Engine Instrument Graphical Data Block provides textual and graphical representation of the percent power EGT CHT and TIT If selected this data block is positioned below the other left data blocks Engine Instruments Data Log The EX5000 Engine...

Страница 304: ...ed in the bottom right button of each page The highest priority and most recent messages appear at the top of the list b Software build number software part number and release date are displayed here Expiration dates for on board databases are also shown on this page c Setup Menu Line select keys to select specific setup functions including Airport Filter Declutter Settings Data Block Editing Syst...

Страница 305: ...Section 7 Columbia 400 LC41 550FG Description of the Airplane and Systems Initial Issue of Manual November 10 2004 RC050002 Latest Revision Level Date A 12 01 2004 7 113 Figure 7 40 3 g f e d c b a ...

Страница 306: ...lect Towered Non Towered or both b Surface Select between hard soft and or water surfaces NOTE Display of airports with both hard surface and water runways requires that the hard surface box be checked c Minimum Runway Length select the minimum runway length from 2000ft 7000ft or show all lengths d Selection Control Use right knob to move the blue field selector e Change Control Use left knob to c...

Страница 307: ... symbol d Range Dots The circles represent the seventeen available map scales A cyan colored circle indicates that the navaid is displayed at that range The vertical dash line indicates that the navaid is displayed at that range The vertical dash line indicates the map current scale Note The 1000NM and 1500NM columns are not displayed because this data is never displayed at these ranges e Selectio...

Страница 308: ...lay Data block automatically resizes based on number of lines selected Data block disappears if all lines are blank c Selection Control Use right knob to move the green field selector d Change Control Use left knob to change the value or status of the selected field e Save Saves settings and returns to main setup page f Cancel Cancels any changes and returns to main setup page 5 System Time The Sy...

Страница 309: ...f the selected field g Save Saves settings and returns to main setup page h Cancel Cancels any changes and returns to main setup page If the MFD time has drifted noticeably from the current GPS time ensure the GPS unit s are receiving valid GPS information and enter the System Time page Change the Time Source setting from Auto to GPS then return the setting to Auto and press the Save button If the...

Страница 310: ... the Datalink system on or off If Broadcast datalink is also installed this setting is labeled Multilink Enabled If this box is not checked subsequent flights will not be shown on your account page at www myavidyne com b Coverage Area Switches weather coverage area between Current Position and Flight Plan c Coverage Radius NM Selects 50 100 200 300 or 400 nautical mile radius around the aircraft o...

Страница 311: ...s Turns graphical and textual METAR reporting on and off g AIRMETs SIGMETs Turns AIRMET SIGMET reporting on and off h SUA Status TFRs Turns the Special Use Airspace SUA and Temporary Flight Restrictions TFRs reporting on or off i Factory Defaults Sets the Datalink Setup to the following values 1 Coverage area Flight Plan 2 Coverage Area 200 NM 3 NEXRAD Resolution Medium 4 Request Interval 20 minut...

Страница 312: ... are transmitting when they are not In this situation reset the Com 1 or Com 2 circuit breakers PICTURE OF THE GMA AUDIO PANEL Figure 7 46 On Off and Fail safe Feature Unit power is turned off by rotating the left small knob counterclockwise into the detent To turn the unit on rotate the knob clockwise past the click The small knob also functions as the pilot or copilot s ICS volume control on the...

Страница 313: ...ull counterclockwise detent position is Off Left large knob Pilot ICS mic VOX squelch level Clockwise rotation increases the amount of mic audio VOX level required to break squelch Full counterclockwise is the hot mic position Right small knob In position Copilot ICS volume Out position Passenger ICS volume Right large knob Copilot and passenger mic VOX squelch level Clockwise rotation increases t...

Страница 314: ...ertain instances to identify an airway There are three lights blue outer marker amber middle marker and white inner airway marker which give a visual and aural indication when the respective marker is crossed in flight In addition to the normal marker beacon functions the GMA 340 provides an audio muting function The lamps illuminate and an associated keyed tone is heard when the MKR audio is sele...

Страница 315: ...nals can be used as a primary means of navigation in oceanic airspace and certain remote areas GPS equipment may be used as a supplemental means of IFR navigation for domestic en route terminal operations and certain instrument approach procedures This approval permits the use of GPS in a manner that is consistent with current navigation requirements The system can be used as one of the required i...

Страница 316: ...n GNS 430 Pilot s Guide and Reference A Garmin GNS 430 Pilot s Guide and Reference is included as part of the delivery kit with the airplane and is the primary source document for operation of the airplane s GNS 430 system To properly use all the features of the GNS 430 GPS requires considerable practice and study However the long term benefits more than justify the time devoted to learning the sy...

Страница 317: ... reset the Com 1 or Com 2 circuit breakers Normal Operations Refer to the Garmin GNS 430 Pilot s Guide and Reference for detailed operation procedures The following items are discussed here for emphasis and clarity Pilot s Displays Both No 1 and No 2 GNS 430 System data will appear on the PFD The source of data is either GPS or VLOC as annunciated on the display above the CDI key on the top GNS 43...

Страница 318: ...ssed again to cycle off When activated the switch illuminates NAV COM BYPASS in blue Activation of the Nav Com Bypass Switch turns on the No 1 GPS No 1 Com and No 1 Nav by connecting them directly to the right battery bypassing the power grid circuit breaker panel and associated wiring Communications is only through the pilot s headset and activated with the pilot s PTT switch The integrity of the...

Страница 319: ...seconds after code entry is complete to return the cursor to the fourth digit The numbers 8 and 9 are not used for code entry only for entering a Count Down time contrast and display brightness and data selection in the Configuration Mode Keys for Other GTX 327 Functions IDENT Pressing the IDENT key activates the Special Position Identification SPI Pulse for 18 seconds identifying your transponder...

Страница 320: ...stallation To view or change any of the GTX 327 configuration parameters you must access the GTX 327 Configuration Mode Use caution when changing configuration When in doubt contact your authorized Garmin Aviation Service Center Your Garmin dealer can assist in configuration changes The Configuration Mode should not be used during flight To use the GTX 327 Configuration Mode 1 Press and hold the F...

Страница 321: ...ponder is located in the lower portion of the radio rack panel assembly The GTX 330 is a radio transmitter and receiver that operates on radar frequencies receiving ground radar or TCAS interrogations at 1030 MHz and transmitting a coded response of pulses to ground based radar on a frequency of 1090 MHz The GTX 330 is equipped with IDENT capability that activates the Special Position Identificati...

Страница 322: ... 7 providing 4 096 active identification codes Pushing one of these keys begins the code selection sequence The new code is not activated until the fourth digit is entered Pressing the CLR key moves the cursor back to the previous digit Pressing the CLR key when the cursor is on the first digit of the code or pressing the CRSR key during code entry removes the cursor and cancels data entry restori...

Страница 323: ...mer begins when liftoff is sensed ALTITUDE MONITOR Controlled by START STOP key Activates a voice alarm and warning annunciator when altitude limit is exceeded OAT DALT Displayed when the GTX 330 is configured with temperature input Displays Outside Air Temperature and Density Altitude COUNT UP TIMER Controlled by START STOP and CLR keys COUNT DOWN TIMER Controlled by START STOP CLR and CRSR keys ...

Страница 324: ...rcraft is on the ground To operate the Count Up timer 1 Press the FUNC key until COUNT UP is displayed 2 If necessary press CLR to reset the Count Up timer to zero 3 Press START STOP to count up 4 Press START STOP again to pause the timer 5 Press CLR to reset the timer to zero To operate the Count Down timer 1 Press the FUNC key until COUNT DOWN is displayed 2 Press CRSR and use the 0 9 keys to se...

Страница 325: ...he airplane s altimeter does not affect the blind encoder However an incorrect altimeter setting will cause the airplane to fly at an altitude different from the assigned altitude and the incorrect or unassigned flight altitude will be displayed on the ground based radar When ATC indicates that the altitude readout is invalid the first thing the pilot should check is the airplane s altimeter setti...

Страница 326: ...sed to add a hand held microphone if desired Only the pilot s side jack is functional when the Nav Com Bypass switch is activated The airplane has special Bose headset plugs which are designed to operate with the active noise reduction ANR headsets The Bose headsets provide a significant reduction in cabin noise Headsets It is suggested that the owner or operator purchase headsets for use in the a...

Страница 327: ...ch the ELT is not activated the unit can be turned on with either the remote switch or the switch on the ELT Do not turn the ELT off even at night as search aircraft may be en route 24 hours per day Turn off the unit only when the rescue team arrives at the landing site Switches There is a two position remote ELT switch located under the knee bolster on the copilot s side which is used to arm test...

Страница 328: ...position The ELT if it is functioning properly should be reset If this procedure does not reset the ELT and a tone is still audible on the communication radio the ELT must be turned off by moving the switch on the transmitter to the neutral position The problem with the ELT shall be corrected in a timely manner Refer to FAR 91 207 for additional information FIRE EXTINGUISHER General The airplane f...

Страница 329: ...dwich The depth of the mesh varies from 10 to 30 thousandths of an inch below the surface of the paint and encompasses most surfaces of the airplane The various parts of the airplane are then interconnected through use of metal fasteners inserted through several plies of mesh mesh overlaps and bonding straps WARNING The thickness of the surface paint is important for lightning protection issues an...

Страница 330: ...red to be used by the pilot above 12 500 ft for flight time exceeding 30 minutes and above 14 000 ft for the duration of the flight above 14 000 ft If climbing to an altitude where oxygen will be required it is recommended that at approximately 10 000 ft the pilot should begin using the oxygen Passengers are required to be supplied with oxygen above 15 000 ft Oxygen Flow Controls Four manually ope...

Страница 331: ...system as the outlet pressure display provides the pilot graphical feedback to the presence of oxygen pressure at the distribution manifold and the flow rate of the oxygen from the system Higher outlet pressures equate to lower altitudes and one user lower outlet pressures equate to high altitudes and four users Problems with oxygen distribution as visualized through low pressure or low flow indic...

Страница 332: ...ng exclusively through the mouth extremely light breathing or nasal blockage will inhibit oxygen flow NOTE Breathing through the nose and limiting conversation is required for the user to achieve proper oxygenation when using nasal cannulas WARNING Do not use oxygen when utilizing lipstick chapstick petroleum jelly or any product containing oil or grease NOTE If the pilot has nasal congestion or o...

Страница 333: ... Figure 7 55 Filler Port The filler port for refilling the oxygen bottles is located on the pilot s side of the hat rack in the aft portion of the baggage compartment The port is placarded Oxygen Fill Port Do Not Exceed 2000 p s i Refer to page 8 8 for details on servicing the oxygen system Flowmeter Valve Flexible Line Flexible Line Flowmeter Altitude Scale Flowmeter ...

Страница 334: ... s Operating Handbook The System Fifty Five X Autopilot can be used for VFR operations as well as precision and non precision approach IFR operations An S TEC System Fifty Five X Autopilot Pilot s Operating Handbook is included as part of the FAA Approved Flight Manual and Pilot s Operating Handbook and is the primary source document for operation of the airplane s autopilot as well as how it is i...

Страница 335: ...avigation source other than GPS is selected on the primary navigation display the autopilot will display a FAIL and a blinking NAV indicating it is no longer following the GPS signal The aircraft will go to wings level flight attitude The remote annunciator will display a blinking NAV A press of the NAV button will disable GPSS and the aircraft will intercept and track the VOR signal PRECISE FLIGH...

Страница 336: ...l not automatically re extend and must be recycled after the following conditions 1 Circuit Breaker Pull 2 Automatic Stowage Due to Asymmetric Deployment or Low Voltage 3 Automatic Stowage Due to Stall Warning Activation CO GUARDIAN CARBON MONOXIDE DETECTOR The Model 452 201 Series Carbon Monoxide Detector is designed to detect measure and provide a visual and aural alert to the pilot before the l...

Страница 337: ...the aircraft s non essential DC power bus the antenna and data port The Wx Receiver also provides an antenna output for connection to an XM Digital Audio receiver if installed The tear drop style antenna receives line of site transmissions from the satellites The antenna consists of a LH circular polarized hemispherical element with an integrated low noise amplifier LNA This LNA is powered by a 5V...

Страница 338: ...AD is advisory only and is a back up to the See and Avoid Concept and the ATC radar environment Additional functions provided by the TCAD are Data and Altitude The TCAD will display the identity transponder code when available and N number Mode S traffic of detected aircraft Traffic Audio from TCAD only if both GTX330 TIS and TCAD are installed When Airspeed switch is grounded aircraft speed less ...

Страница 339: ...longer See Figure 7 60 for TA thresholds SL A when the TCAD is in Approach or Departure Mode automatically activated when flaps are deployed See Figure 7 61 for TA thresholds SL B for all other flight conditions Host to Intruder Intruder Type Tau seconds Range nm Altitude Separation ft Altitude reporting intruders 20 0 20 600 Non altitude reporting intruders 15 0 20 N A Figure 7 60 Host to Intrude...

Страница 340: ...cement mute button and annunciator acknowledge button A single press of the button mutes a TA announcement in progress A double press of the button repeats any TA announcement with updated information and the range of the intruder If no TAs are in effect when the button is double pressed the TCAD announces No Advisories TCAD Display on the Avidyne Entegra MFD Refer to the Avidyne Flightmax EX5000 ...

Страница 341: ...itive Mixture Table 8 5 Grounding During Refueling and Defueling 8 5 Fuel Contamination 8 6 Oil Servicing 8 7 Oil Grades Recommended for Various Temperature Ranges 8 7 Sump Capacity 8 7 Oil Filter 8 7 Brakes and Tire Nose Strut Pressures 8 7 Tire Considerations 8 7 Battery Replacement Cycles 8 8 Oxygen System Servicing 8 8 MAINTENANCE AND DOCUMENTATION 8 10 Maintenance 8 10 Airplane Inspection Per...

Страница 342: ...e up to 90 days 8 15 Return to Service from Temporary Storage 8 16 Indefinite Storage over 90 days 8 16 Return to Service from Indefinite Storage 8 17 Airframe Preservation for Temporary and Indefinite Storage 8 17 Airframe Preservation Return to Service 8 18 Inspections During Temporary Storage 8 18 Inspections During Indefinite Storage 8 18 AIRFRAME AND ENGINE CARE 8 19 Airframe 8 19 Exterior 8 ...

Страница 343: ... will facilitate compliance It is recommended that the owner or operator of the airplane contact a dealer or a certified service station for service information All correspondence regarding the airplane should include the airplane serial number Fuselage Identification Plate The airplane serial number make model Type Certificate TC number year of manufacture and Production Certification PC number i...

Страница 344: ...manufacturer at the address shown on page 8 3 Publications are also available for purchase by non owners Pilot s Operating Handbook and FAA Approved Flight Manual 1 Normal Procedures Checklist 1 Columbia 400 Electrical Manual Emergency Procedures Checklist 1 Columbia 400 Passenger Briefing Card 4 ADLOG MRS 1 Columbia 400 Maintenance Manual Lancair Warranty Program 1 In addition to the items listed...

Страница 345: ...5 56 8 57 6 2 9 41 155 2 157 4 7 9 16 60 6 61 4 3 1 42 159 0 161 3 8 1 17 64 4 65 3 3 3 43 162 8 165 1 8 3 18 68 1 69 1 3 5 44 166 5 169 0 8 4 19 71 9 73 0 3 6 45 170 3 172 8 8 6 20 75 7 76 8 3 8 46 174 1 176 6 8 8 21 79 5 80 6 4 0 47 177 9 180 5 9 0 22 83 3 84 5 4 2 48 181 7 184 3 9 2 23 87 1 88 3 4 4 49 185 5 188 2 9 4 24 90 8 92 2 4 6 50 189 3 192 0 9 6 25 94 6 96 0 4 8 51 193 0 195 8 9 8 26 98...

Страница 346: ...ntroduced to the fuel system 1 sediment such as dirt and bacteria 2 water and 3 the improper grade of fuel 1 The accumulation of sediments is an inherent issue with most aircraft and can never be completely eliminated Refueling the airplane at the conclusion of each flight and using fuel from a supplier who routinely maintains the filtration of the refueling equipment will lessen the problem somew...

Страница 347: ...move from the filler neck Oil Grades Recommended for Various Average Air Temperature Ranges Below 40 F 4 C SAE 30 10W30 15W50 or 20W50 Above 40 F 4 C SAE 50 15W50 or 20W50 Sump Capacity The system has a wet type oil sump with a drain refill capacity of eight quarts Oil Filter A full flow spin on type 20 micron oil filter is used NOTE There are a number of oil additives on the market that are formu...

Страница 348: ...he system batteries indicate their charge on the installed voltmeter and ammeter the ELT battery does not have a positive test to indicate its charge The table below summarizes the replacement cycles BATTERY REPLACEMENT CYCLES BATTERY TYPE BATTERY LOCATION REPLACEMENT CYCLE Emergency Locator Transmitter ELT Alkaline Type Battery Aft of the baggage compartment hat rack Please see page 7 135 for mor...

Страница 349: ...upply is filled NOTE This fixed oxygen system has a maximum bottle pressure of 2 000 psi 6 When the system is filled to the intended capacity set the Oxygen Switch to ON 7 Ensure that the Outlet Pressure Display green indication is illuminated 8 Set the Oxygen Switch to OFF 9 Set the Left Bus switch to OFF 10 Ensure safety cap is installed over the filler port See the Columbia 400 Maintenance Manu...

Страница 350: ...e center Alterations or Repairs All alterations or repairs to the airplane must be accomplished by licensed personnel In addition an alteration may violate the airworthiness of the airplane Before alterations are made the owner or operator of the airplane should contact the FAA for approval Required Oil Changes and Special Inspections During the engine break in period Non dispersant mineral oil co...

Страница 351: ...ntenance facility may be permitted but the owner or operator of the airplane must obtain permission from TLC prior to engaging a non approved facility Warranty work by a non approved maintenance provider must be obtained for each warranty incident That is an approval by TLC for a specific issue does not constitute blanket permission AIRPLANE DOCUMENTATION There are certain items required to be in ...

Страница 352: ...4 This system is the best available and ensures that the maintenance history of the airplane and all applicable ADs are precisely documented in a logical format The system has been in use for more than 20 years and is revered by both mechanics and Part 135 operators The ADLOGTM service also includes ADs for STC equipment that the owner may add to the airplane ...

Страница 353: ...ch the wheel pant It is recommended that the airplane only be maneuvered during towing by use of the hand held tow bar If it is necessary to tow with a vehicle extreme care is required to ensure the rotation limits of the nose wheel 60 left and right are not exceeded Since the rotation of the nose gear is limited by physical stops rotating the gear beyond 60 will damage the airplane It is always a...

Страница 354: ...use of a windshield cover is an often debated issue and is a decision the owner or operator of the airplane must make Windshield covers have both positive and negative benefits Ultimately a number of factors must be weighed including 1 the geographical area of operations 2 the time of year 3 the specific parking location and 4 the integrity of the covering device 1 From a positive standpoint the c...

Страница 355: ...the control lock 4 topping off the fuel tanks 5 cleaning the bolts and nuts on the brakes and applying a non stick preservative like graphite or a silicone and 6 installing other owner option protection devices There are three types of storage categories flyable temporary and indefinite The time period and applicable storage procedure for each type is discussed below Flyable Storage 5 to 30 days I...

Страница 356: ...oil 3 Reinstall the spark plugs according to manufacturer s recommendations 4 Conduct a normal engine start and idle the engine for several minutes until oil temperature is within normal limits Monitor engine instruments to ensure they are within normal operating ranges 5 Stop the engine and inspect the entire airplane before test flying Indefinite Storage Over 90 Days If the airplane is to be sto...

Страница 357: ...eller several times to remove the preservation oil 4 Apply Champion thread lubricant to spark plugs in accordance with the manufacturer s instructions Install and torque the spark plugs 300 to 360 in lbs 5 Rotate the propeller by hand through the compression strokes of all the cylinders to check for possible liquid lock 6 Conduct a normal engine start and idle the airplane for several minutes unti...

Страница 358: ... has been in storage for a long period the date of the required annual inspection may have passed There is no requirement to perform this inspection during the temporary or indefinite storage period However the inspection must be completed before than airplane is returned to service Inspections During Temporary Storage The following inspections should be performed while the airplane is in temporar...

Страница 359: ...he tape on the wing when entering the aircraft People who sit on the wing by lifting themselves up over the leading edge should take care not to drag their legs over the tape when sliding on or off the wing If the tape is starting to fray detach crack crinkle etc it should be replaced using the instructions in the maintenance manual Windshield and Windows The proper care of the windshield and wind...

Страница 360: ...o remove difficult substances such as tape residue oil and grease the safest solvents are 100 mineral spirits or kerosene Some alcohols are safe such as isopropyl alcohol Interior Cleaning and Care The useful life of the airplane s interior can be extended through proper care and cleaning One of the major elements in the aging process is the interior s exposure to sunlight If possible the airplane...

Страница 361: ...ally designed for this use Care must be exercised to ensure that application of the solvent does not damage other components in the engine area Refer to the Lancair Columbia 400 LC41 550FG Approved Maintenance Manual for additional instructions Propeller Cleaning and Care It is important to keep the propeller clean since it facilitates detection of cracks and other problems The propeller must be c...

Страница 362: ...Section 8 Handling Servicing and Maintenance Columbia 400 LC41 550FG RC050002 Initial Issue of Manual November 10 2004 8 22 Latest Revision Level Date 11 10 2004 This Page Intentionally Left Blank ...

Страница 363: ...n the Lancair Information Manual for the Columbia 400 the actual supplements provided by the holder of the STC are not included However to assist the reader in understanding the special equipment that is installed through an STC a discussion of these components is included on the following pages A generic format is used for each supplemental section since this will provide a consistent form of pre...

Страница 364: ...he airplane Lancair neither endorses nor opposes after market installations however such an installation can limit or invalidate the warranty on the airplane Lancair does not provide technical support or documentation for after market installations The holder of the STC normally provides these services This log is provided as a service to the owner or operator of the airplane so that after market ...

Отзывы:

Нет отзывов

Похожие инструкции для Columbia 400

Freeride Series

Бренд: F-One Страницы: 21

Бренд: Carl Goldberg Products Страницы: 10

Бренд: Carl Goldberg Models Страницы: 24

Бренд: Mountain Models Страницы: 19

Бренд: DOVA AIRCRAFT Страницы: 78

Бренд: SKY PARAGLIDERS Страницы: 35

Бренд: Ozone Страницы: 2

Бренд: Ozone Страницы: 18

Бренд: Diamond Aircraft Страницы: 24

ZODIAC CH 601 Series

Бренд: Zenith Страницы: 25

Бренд: ACME Страницы: 18

Бренд: Staufenbiel Страницы: 27

Бренд: ROBBE Страницы: 16

Super Star 3113

Бренд: ROBBE Страницы: 24

Бренд: ROBBE Страницы: 48

Бренд: PLKB Страницы: 24

Glider Dual Fuse Fox

Бренд: MicronWings Страницы: 4

Бренд: Axis Страницы: 22

Бренды по названию

0 1 2 3 4 5 6 7 8 9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Популярные бренды

Загрузить еще бренды