LX Series Unit Ventilator Controller User's Guide
58
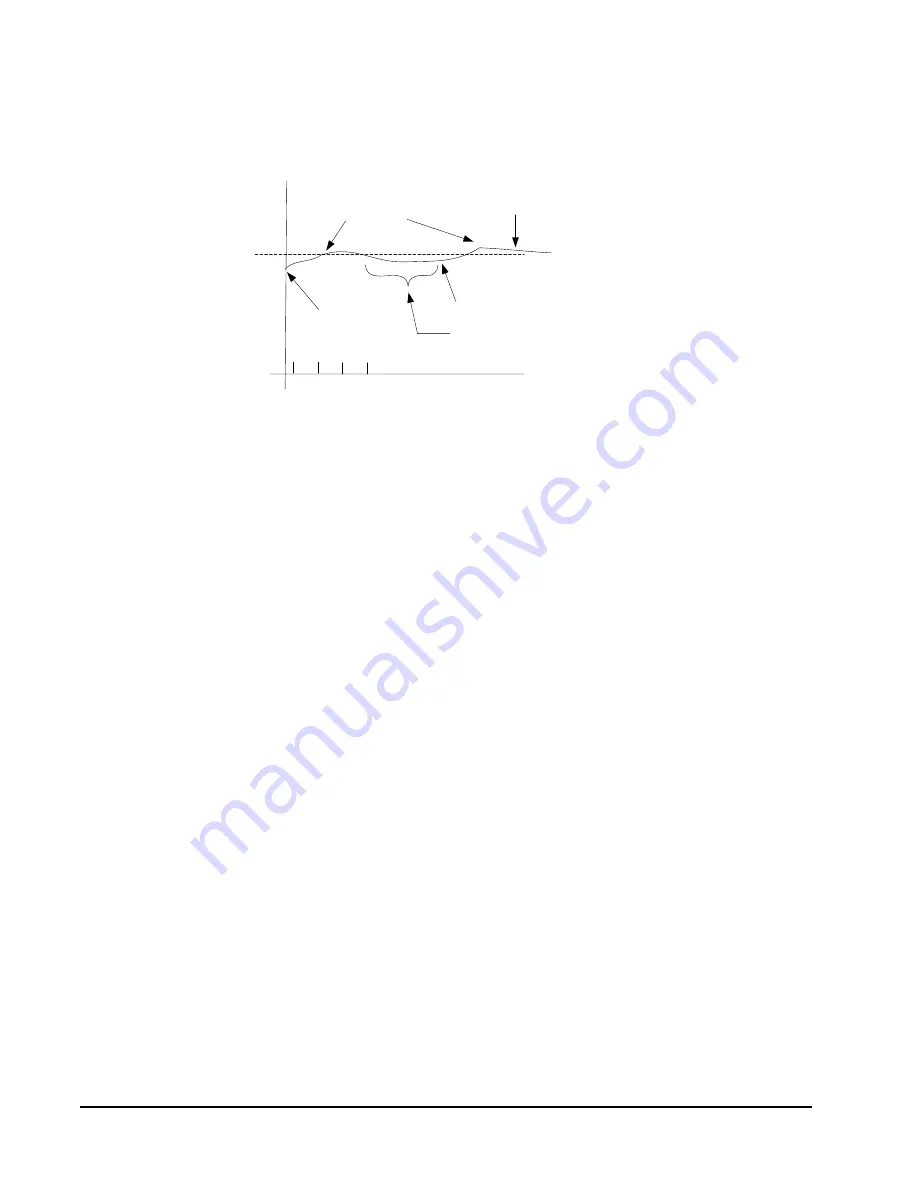
However, with a proportional integral controller, the error would accumulate over
time. Periodically, a portion of the error would be added back into the error. Error
would accumulate and would finally be large enough to turn on the heat. See
Figure 24.
Derivative
Derivative control opposes sudden changes in the input value. Whereas integral
control is able to correct errors that persist over time, derivative control can
respond to sudden changes quickly.
Consider a graph of temperature over time. Because the derivative of a function is
the rate of change of the function, the derivative of temperature over time is the
rate of change of the temperature per unit time. For example, rate of change could
be degrees per minute.
Derivative control opposes the rate of change. For example, consider a hospital
lobby in the arctic. Because the lobby changes temperature often, it has its own
local heaters that are controlled by a PID loop. Every time the hospital doors open,
the temperature in the lobby quickly decreases. This sudden drop in temperature is
a considerable rate of change. This considerable rate of change is opposed by the
derivative control. The derivative control increases the output of the PID loop that
increases the output of the heaters. As the lobby temperature becomes closer to the
setpoint, the derivative control output decreases to zero as the lobby temperature
reaches its setpoint.
Gain
The derivative gain is the amplification of the derivative output. The gain is
measured as a percentage per unit of change where a unit is a Centigrade or
Fahrenheit degree. If 50 is entered into the Gain box, then each unit of error causes
a 50% increase in derivative control output.
T
e
mperat
u
re
Time
Setpoint
Heat is ON
Heat is OFF.
Heat is ON.
8:00 8:30 9:0010:00
Error accumulates.
Space
Temperature
Figure 24: Heating Using a PI Controller
















































