www.iOptron.com
32
TIP:
Celestial sphere is an
imaginary sphere of
infinite radius.
NOTE:
You need two numbers
to define a position on
the celestial sphere.
To understand the celestial coordinate systems there are
several concepts that should be clarified.
The
Celestial sphere
is an imaginary sphere of infinite radius
concentric with the earth on which all celestial bodies are
assumed to be projected.
Celestial coordinates
are used to
define a point on the celestial sphere. A
great circle
, a.k.a.,
orthodrome, is the intersection of a sphere and a plane
through its center. For the celestial sphere, a great circle is
the intersection of a plane through the observer (on the earth)
and the celestial sphere.
Celestial pole
is either of the two
points of intersection of the celestial sphere and the extended
axis of the earth. There are two celestial poles--the
north
celestial pole
and the
south celestial pole.
The
Zenith
is
the point of the celestial sphere vertically overhead. The
Nadir
is the point on the celestial sphere vertically below the
observer, or 180 degrees from the zenith. A
horizon
is a
great circle on the celestial sphere midway between the
zenith and nadir.
Celestial meridian
is a great circle of the
celestial sphere through the celestial poles and the zenith.
Celestial equator
is the intersection of the extended plane of
the equator and the celestial sphere. It is the primary great
circle of the celestial sphere in the equatorial system,
everywhere 90-degree from the celestial poles.
We will talk about two different kinds of celestial coordinate
systems. One is the
altazimuth
system. And the other is the
equatorial
system. The major difference between them is the
referencing great circle. In
altazimuth
it is the celestial
horizon, while in
equatorial
it is the celestial equator.
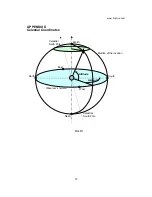
To define a position on the celestial sphere, we need two
angles. In the
altazimuth
system (FIG. D1) these two angles
are
altitude (A)
and
azimuth (Z).
Imagine a vertical plane
perpendicular to the observer’s horizon that passes through
the observer and the star. The intersection of the vertical
plane and the observer’s plane of horizon defines the
azimuth
. It is measured from the south (or the north) to the
intersection (in the direction of motion of the star, in degrees,
0
°
~360
°
). In GoToNova
TM
azimuth is measured from the north.
On the vertical plane,
altitude
is measured from the
intersection to the direction of the star (also in degrees, -
90
°
~90
°
).
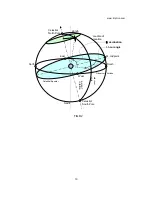
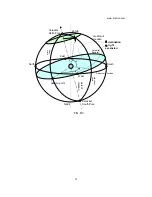
In the
equatorial
system (FIG. D2 and D3),
hour angle (t)
is
measured on the equator from the point of intersection of the
celestial equator and the local meridian in the direction of
motion of the star. The value of hour angle is measured in
hours, minutes and seconds instead of degrees.