2-4 Examining operating status
Selection guidelines
2-10
1
2
3
4
5
6
7
8
9
10
11
Apx
Se
lec
tion gui
de
lin
es
Examining effective torque and average rotation speed
One way to check if the heat generated from the actuator during operation would present a problem is
to determine if the point of operation, determined by the effective torque and average rotational speed,
is inside the continuous motion range explained in [1-13 Operable range] (1-15).
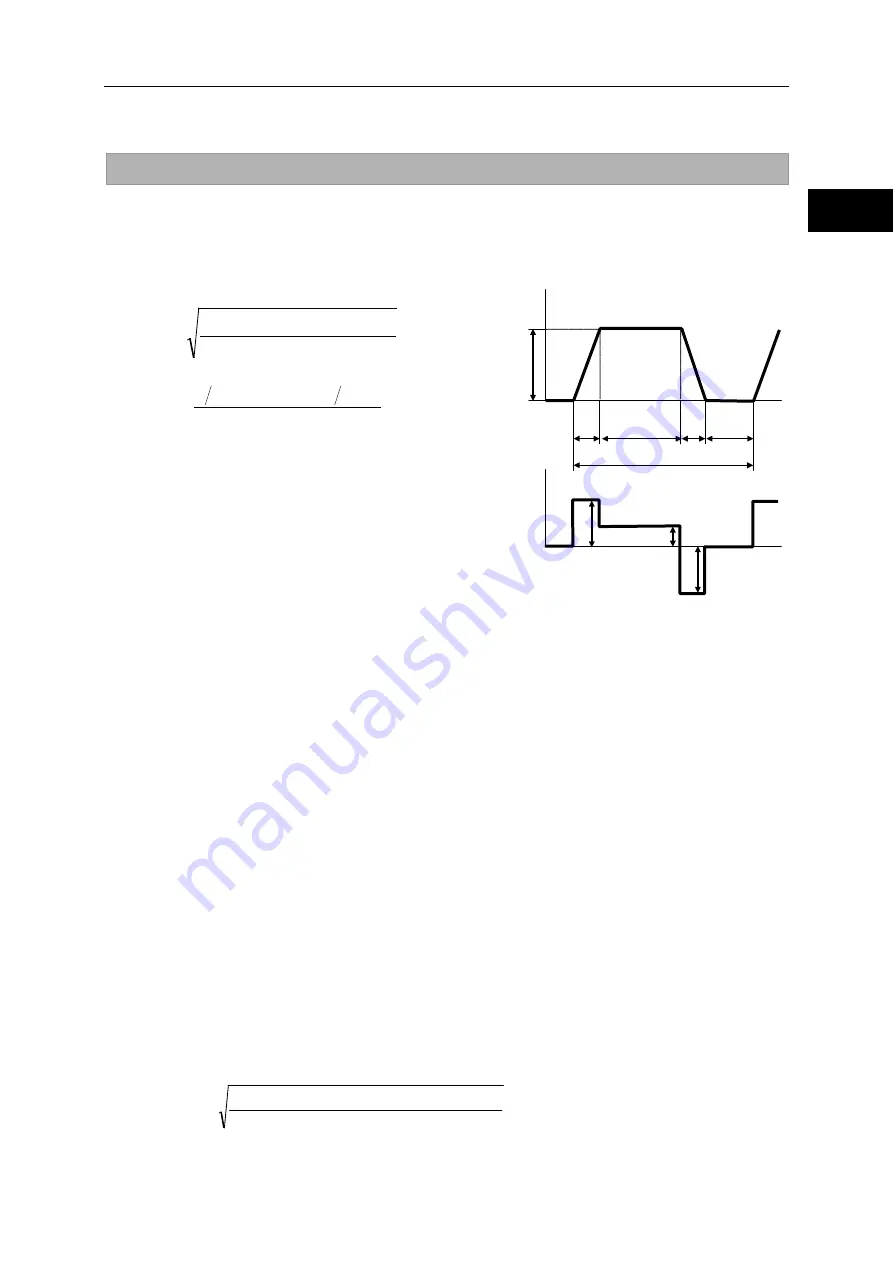
Using the following formula, calculate the effective torque Tm and average rotational speed N
av
when
the actuator is operated repeatedly in the drive pattern shown to the right.
t
a
: Acceleration time from speed 0 to N
[s]
t
d
: Deceleration time from speed N to 0
[s]
t
r
: Operation time at constant speed N
[s]
t : Cycle time
[s]
T
m
: Effective torque
[N
・
m]
T
a
: Torque during acceleration
[N
・
m]
T
r
: Torque at constant speed
[N
・
m]
T
d
: Torque during deceleration
[N
・
m]
N
av
: Average rotational speed
[r/min]
N : Rotational speed at constant speed
[r/min]
Calculation example 2
The calculation method is explained below using FHA-11C-50 as an example.
Operating conditions: Accelerate an inertia load and then let it move at a constant speed,
followed by deceleration, based on conditions similar to those used in calculation example 1.
The travel angle per cycle is 120° and the cycle time is 0.8 seconds.
(1)
The travel angle is calculated from the area of the rotational speed vs. time diagram shown
above. In other words, the travel angle
θ
is calculated as follows:
θ = (N / 60)
× {t
r
+ (t
a
+ t
d
) / 2} × 360
Accordingly, tr = θ
/ (6 × N) - (ta + td) / 2
When θ =
120° and
ta = 0.072 [s]
td = 0.047 [s]
N = 100 [r/min]
in calculation example 1, are applied to this formula, tr is calculated as 0.069 seconds.
(2)
Next, calculate the torque during acceleration and torque during deceleration. Based on the
acceleration/deceleration time formulas in the preceding section, the relational expressions
for torque during acceleration and torque during deceleration if k = 1 are as follows:
T
a
= (J
A
+ J
L
) × 2 ×
π
/ 60 × N / t
a
+ T
L
T
d
= (J
A
+ J
L
) × 2 ×
π
/ 60 × N / t
d
- 2 × T
F
- T
L
When the values in calculation example 1 are applied to this formula,
T
a
= 2.30 [N
・
m] and
T
d
= 2.53 [N
・
m]
are obtained.
(3)
Calculate the effective torque. Apply the values in (1) and (2), T
r
= 0 N
・
m, and t = 0.8
seconds to the above formulas.
t
t
T
t
T
t
T
T
d
2
d
r
2
r
a
2
a
m
×
+
×
+
×
=
t
t
2
N
t
N
t
2
N
N
d
r
a
av
×
+
×
+
×
=
Time
Tr
ts: Stopped time
Ta, Tr, Td: Output torques
ta
td
N
tr
Time
Rotational speed
t: Cycle time
ts
Ta
Tor
que
Td
m]
[N
3.19
0.8
0.047
2.53
0.141
0
0.072
8.3
T
M
2
2
2
⋅
=
×
+
×
+
×
=
















































