Danfoss VLT AHF 005, Руководство по конструкции

Страница: 12 / 156

1
1 2 3 4 5 6 7
0.
0
0
-
-
1
1 2 3 4 5 6 7
0.
0
0
-
-
130BB539.10
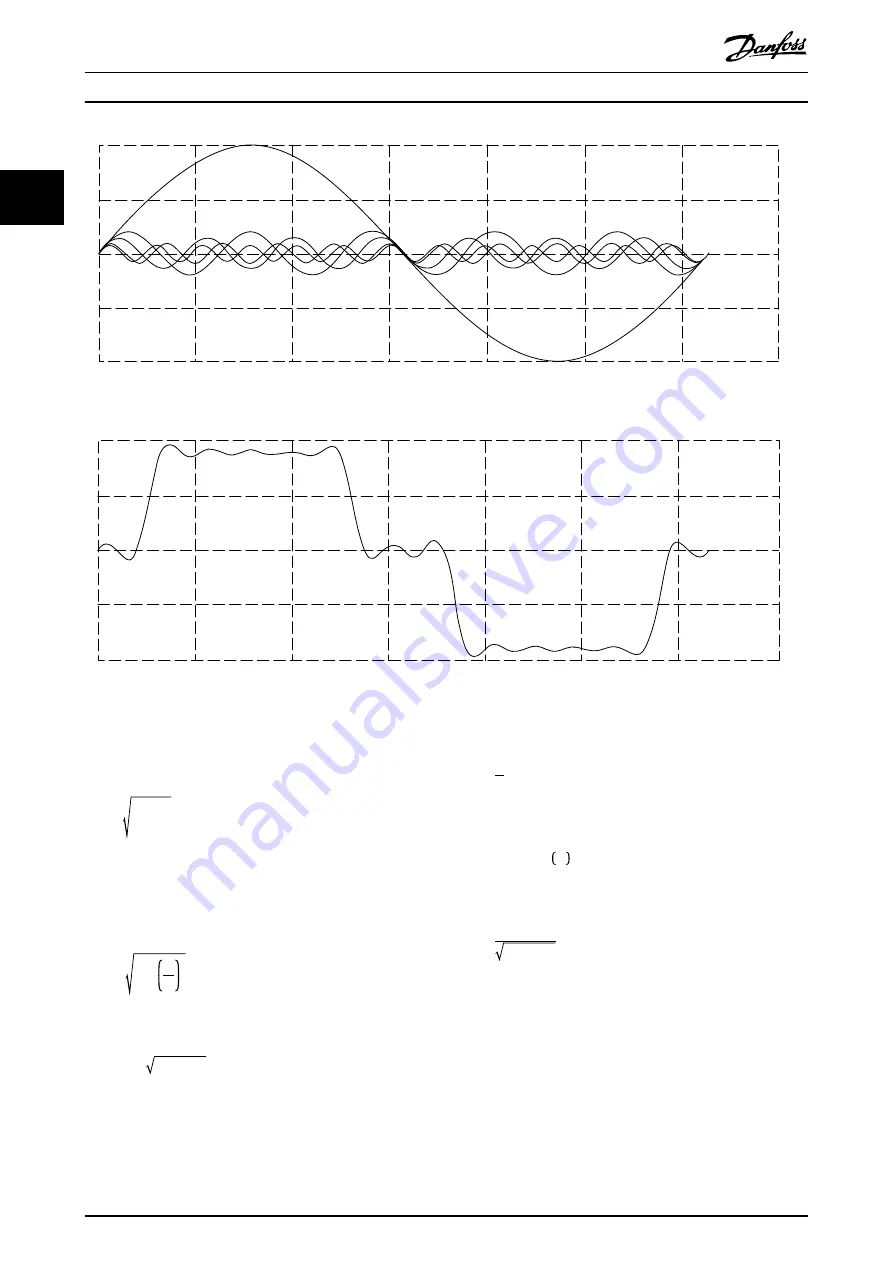
Illustration 2.3 Sinusoidal Waveforms
The integer multiples of the fundamental frequency
ω
1 are
called harmonics. The RMS value of a non-sinusoidal
waveform (current or voltage) is expressed as:
I
RMS
=
∑
h = 1
h
max
I
(h)
2
The number of harmonics in a waveform gives the
distortion factor, or total harmonic distortion (THD). The
THD is given by the ratio of RMS of the harmonic content
to the RMS value of the fundamental quantity, expressed
as a percentage of the fundamental:
THD =
∑
h = 2
h
max
I
h
I
1
2
× 100 %
Using the THD, the relationship between the RMS current
I
RMS
and the fundamental current I
1
can be expressed as:
I
RMS
= I
1
× 1 + THD
2
The same applies for voltage.
The true power factor PF (
λ
) is:
PF = PS
In a linear system, the true power factor is equal to the
displacement power factor:
PF = DPF = cos ϕ
In non-linear systems, the relationship between power
factor and displacement power factor is:
PF =
DPF
1 + THD
2
Reactive power decreases the power factor and harmonic
loads. A low power factor results in a high RMS current
that produces higher losses in the supply cables and
transformers.
In the power quality context, the total demand distortion
(TDD) term is often encountered. The TDD does not
characterize the load, but it is a system parameter. TDD
expresses the current harmonic distortion in percentage of
the maximum demand current I
L
.
Introduction to Harmonics a...
VLT
®
Advanced Harmonic Filter AHF 005/AHF 010
10 Danfoss A/S © 10/2016 All rights reserved. MG80C502
2 2