Casio fx-FD10 Pro, Руководство пользователя

Страница: 75 / 222

3-45
u
Determinant
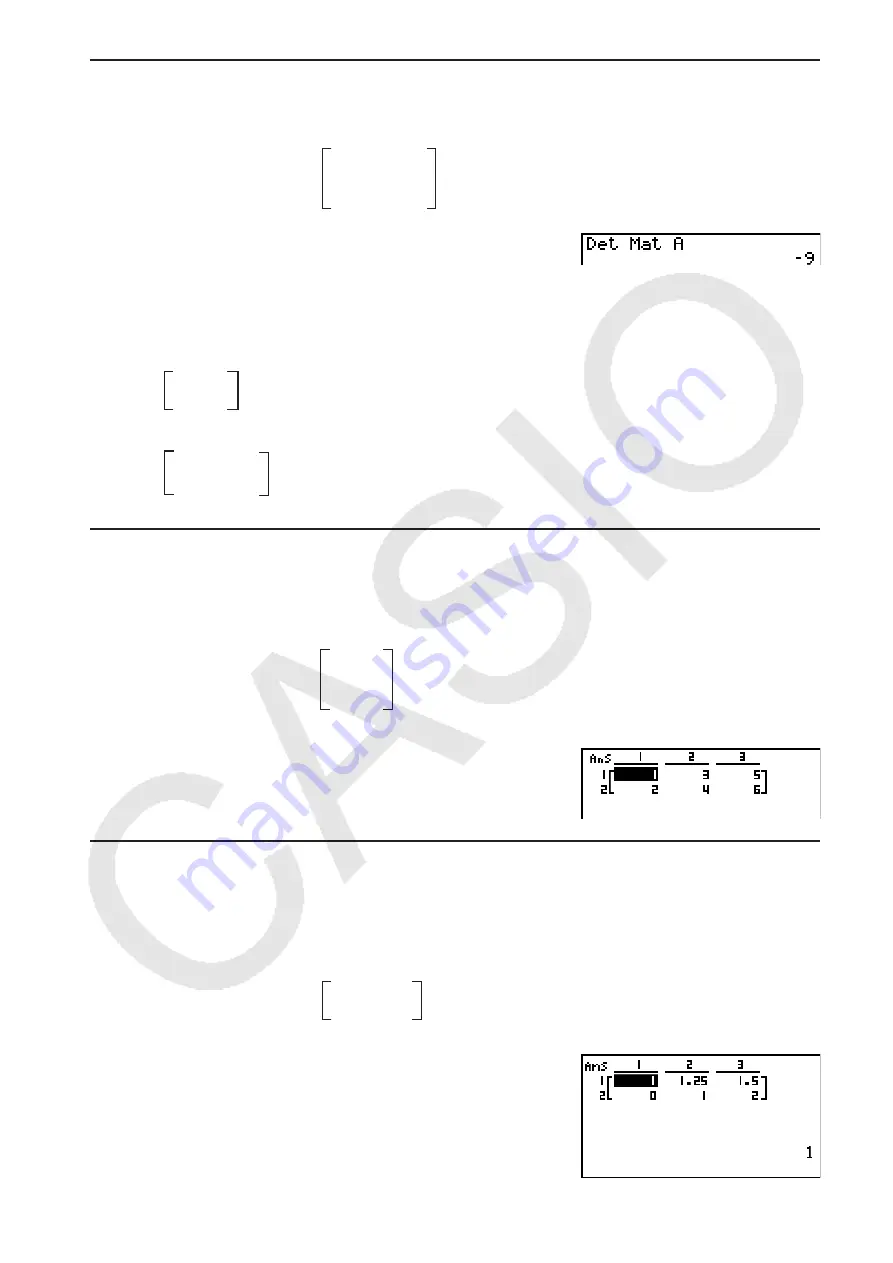
[OPTN] - [MAT] - [Det]
Example Obtain the determinant for the following matrix:
Matrix A =
1 2 3
4 5 6
−1 −2 0
K
2
(MAT)
3
(Det)
1
(Mat)
a1
(A-E)
1
(A)
w
• Determinants can be obtained only for square matrices (same number of rows and columns).
Trying to obtain a determinant for a matrix that is not square produces an error.
• The determinant of a 2
×
2 matrix is calculated as shown below.
| A | =
a
11
a
12
= a
11
a
22
– a
12
a
21
a
21
a
22
• The determinant of a 3
×
3 matrix is calculated as shown below.
= a
11
a
22
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
– a
11
a
23
a
32
– a
12
a
21
a
33
– a
13
a
22
a
31
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
| A | =
u
Matrix Transposition
[OPTN] - [MAT] - [Trn]
A matrix is transposed when its rows become columns and its columns become rows.
Example To transpose the following matrix:
Matrix A =
1 2
3 4
5 6
K
2
(MAT)
4
(Trn)
1
(Mat)
a1
(A-E)
1
(A)
w
u
Row Echelon Form
[OPTN] - [MAT] - [Ref]
This command uses the Gaussian elimination algorithm to find the row echelon form of a
matrix.
Example To find the row echelon form of the following matrix:
Matrix A =
K
2
(MAT)
6
(
g
)
4
(Ref)
6
( g )
1
(Mat)
a1
(A-E)
1
(A)
w
1 2 3
4 5 6
1 2 3
4 5 6