DSO
3
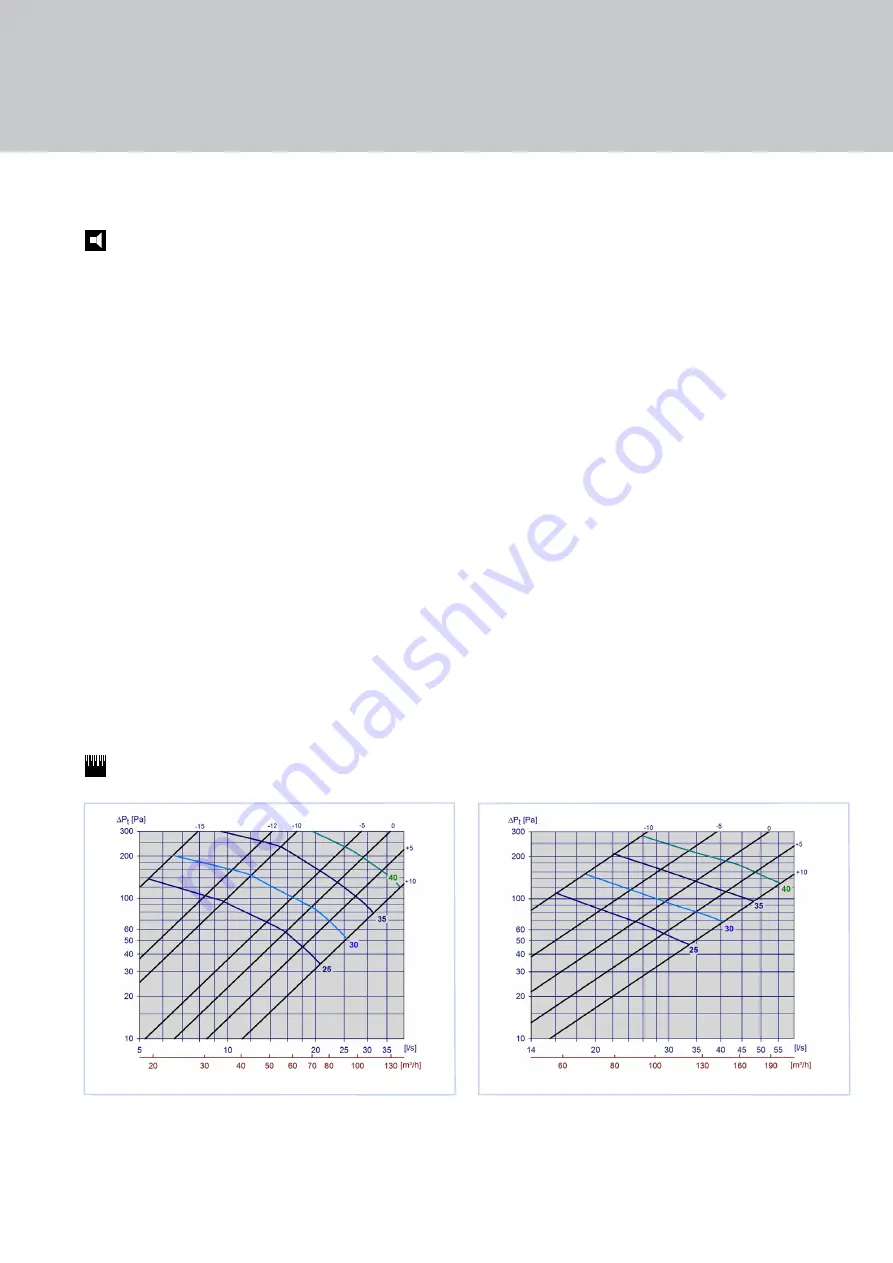
ACOUSTIC DATA
The diagrams provide a summary of the A-weighted sound power level
from diffuser, L
WA
. Correction factors in table 5 are used to calculate
emitted sound power level at the respective frequencies, L
W
= L
WA
+
KO. A room with absorption equivalent to 10m² Sabine will have a
sound pressure level which is 4dB below the sound power level emitted.
Example
:
Office premises require an indoor air extraction of 25 l/s, and for this
purpose a DSO Ø100 extract air terminal device is used.
Room attenuation is 6dB, and the centre cone is to be choked to 80 Pa
total pressure loss.
We aim to find:
a) Emitted sound power level from the valve at 250 Hz, at chosen
working point.
b) A-weighted sound pressure level in the room with the centre cone
in +10 position.
c) A-weighted sound pressure level in the room with centre cone
choked.
Solution:
DSO Ø100, required air flow rate 25 l/s. According to diagram 1 the
emitted sound power will read L
WA
= 29dB(A) for po10 mm,
with a total pressure loss of 50Pa.
a) Table 1 shows that the correction factor for open damper at
250 Hz is -2dB. L
W
at 250 Hz is thus:
L
WA
+ KO =29 + (-2) = 27dB
b) A room attenuation equivalent to 6dB provides a sound pressure
level in the room of: 27 – 6 = 21dB(A)
c) With 30 Pa chocking we reach 80 Pa, and the diagram shows
an increase in L
WA
of 5dB. The sound pressure level is thus:
21 + 5 = 26dB(A)
CALCULATION DIAGRAMS
Diagram1, DSO Ø100
Diagram 2, DSO Ø125





