- 3 -
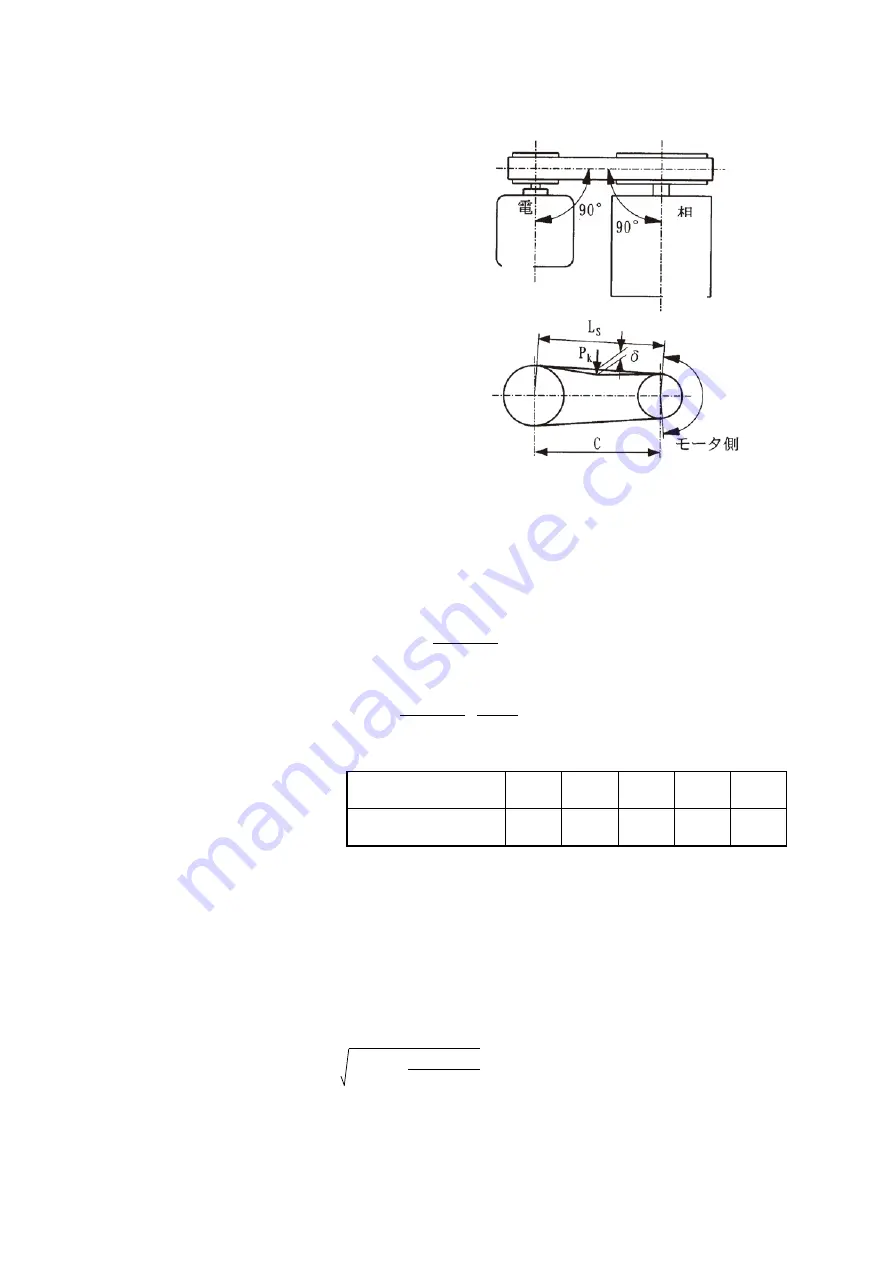
(3) In case of belt drive
Set the counterpart machine shaft and motor
shaft accurately parallel and apply the belt in
such a way that both pulley centers coincide each
other.
The belt is apt to be stretched too much however,
excessive stretching will damage the bearing and
cause unexpected accidents such as breakage of
motor shaft, etc., to which please pay attention.
1) Belt stretching method
Step 1 : Firstly, find the belt span (Ls). Belt span
is the length of the portion of belt
between contact points with both pulleys.
Step 2 : Apply the force ( Pk ), which is required
for deflection ( δ ), at the center of the
belt span. This required force for
deflection ( δ ) should be calculated by
the formula 5 shown below and it should
be within the range of Pk1 - Pk2.
Step 3 : Stretch the belt in such a way that the
deflection ( δ ), when the force is applied,
will be the value found by the following
formula.
δ
= 0.016
・
Ls
2) Calculation formula
Step 1 : How to find belt contact angle (small pulley side) ... Formula 1
Formula 1
θ = 180°
-
2 sin
-1
Step 2 : How to find initial tension (Fo) .................................. Formula 2
Formula 2
Fo = 0.9 { 500 ( ) + m
・
v
2
}
Fo : Initial tension (N)
Table 1
K
θ
: Contact angle
correction factor
Contact angle (
θ
)
140
°
150
°
160
°
170
°
180
°
P
d
: Design power (kW)
Correction factor (K
θ
)
0.89
0.92
0.95
0.98
1
P
d
= P
N
x ( Ko + Ki )
P
N
: Load power (motor output, in general) (1kW)
Ko : Load correction factor (1.0
~
1.5)
Ki : Idler correction factor (0
~
0.2)
Z : Number of belt v : Belt speed (m/sec) m : Mass/unit of belt (kg/m)
Note) Determine Ko, Ki depending on the machine to be used and operation time,
referring JIS Standard or catalog, etc. of belt maker.
Step 3 : How to find span (Ls) ................................. Formula 3
Formula 3
Ls : Span (mm)
C : Distance between shafts (mm)
d
2
: Large pulley nominal diameter
(mm)
d
1
: Small pulley nominal diameter
(mm)
Z
・
v
P
d
d
2
-
d
1
2C
Mo
to
r
C
ount
er
pa
rt
m
ac
hi
ne
Motor side
pulley
θ(Belt cont-
act angle)
Fig. 3 Belt stretching method
2.5 – K
θ
K
θ
Ls = C
2
-
(d
2
-
d
1
)
2
4
























