EL-9600/9400 Graphing Calculator
9-1
Graphing Rational Functions
A rational function
f
(
x
) is defined as the quotient
where
p
(
x
) and
q
(
x
) are two
polynomial functions such that
q
(
x
)
≠
0. The domain of any rational function consists of all
values of
x
such that the denominator
q
(
x
) is not zero.
A rational function consists of branches separated by vertical asymptotes, and the values of
x
that make the denominator
q
(
x
)
=
0 but do not make the numerator
p
(
x
)
= 0
are where
the vertical asymptotes occur. It also has horizontal asymptotes, lines of the form
y = k
(
k,
a constant) such that the function gets arbitrarily close to, but does not cross, the horizontal
asymptote when |
x
| is large.
The
x
intercepts of a rational function
f
(
x
), if there are any, occur at the
x
-values that make
the numerator
p
(
x
), but not the denominator
q
(
x
), zero. The
y
-intercept occurs at
f
(0).
There may be differences in the results of calculations and graph plotting depending on the setting.
Return all settings to the default value or to delete all data.
Set the zoom to the decimal window:
*
(
*
)
*
Before
Start
Notes
Step & Key Operation
(When using EL-9600)
*Use either pen touch or cursor to operate.
Display
(When using EL-9600)
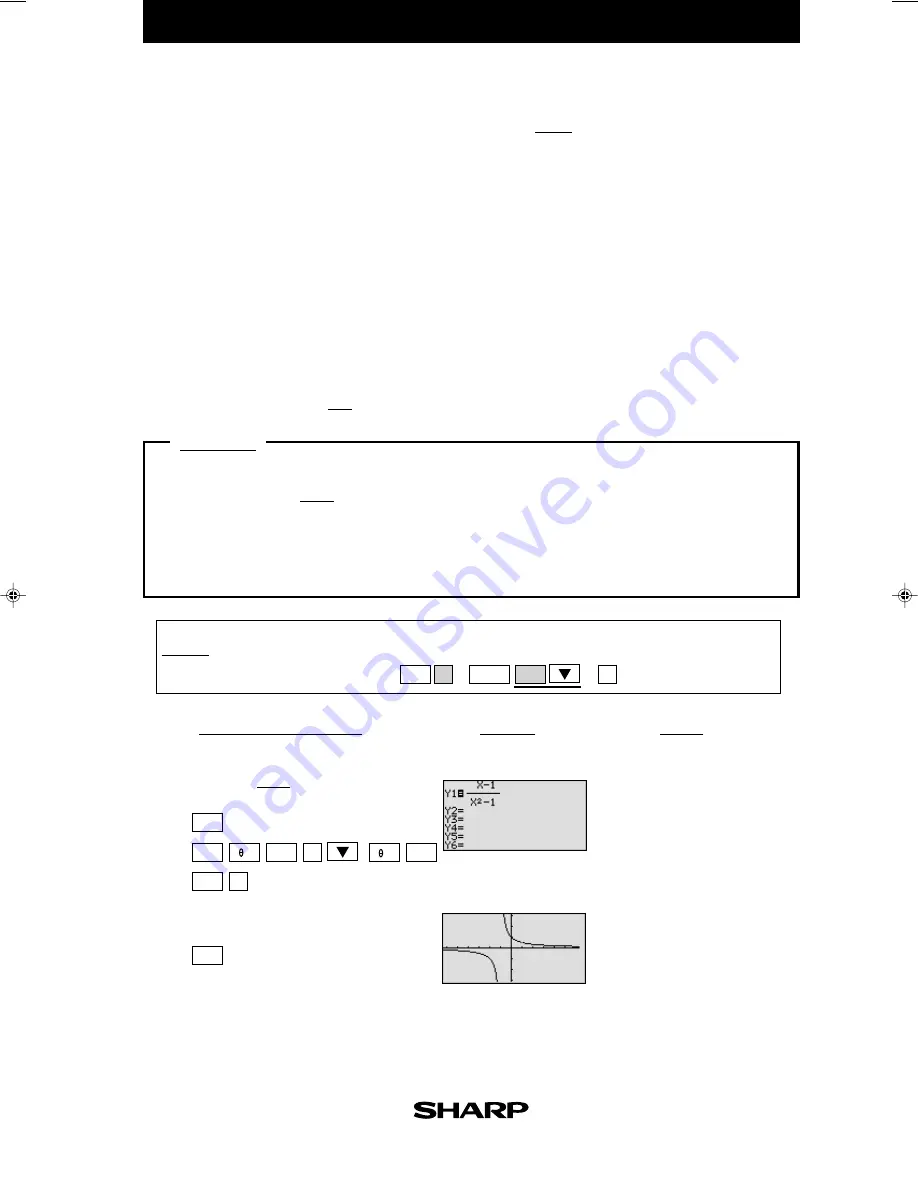
Graph the rational function and check several points as indicated below.
Example
1.
Graph
f
(
x
)
=
.
2.
Find the domain of
f
(
x
)
,
and the vertical asymptote of
f
(
x
)
.
3.
Find the
x-
and
y-
intercepts of
f
(
x
)
.
4.
Estimate the horizontal asymptote of
f
(
x
)
.
1
-
1
Enter
y
= for Y1.
*
x
- 1
x
2
-1
1
-
2
View the graph.
The function consists of two
branches separated by the verti-
cal asymptote.
○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○ ○
q
(
x
)
p
(
x
)
x-
1
x
2
-
1
GRAPH
Y=
A
ENTER
a/b
ALPHA
x
2
ZOOM
—
7
1
1
—
X
/
/
T
/
n
X
/
/
T
/
n
HB1.DocD.
98.10.1, 6:12 PM
6






























