Model No. ME-9858
Physical Pendulum Accessory
9
®
3.Angular Momentum
The linear momentum (p) of the car is m
o
v
o
, but in a collision that causes rotation, we have to
look at the angular momentum
, where r is the distance from the car (rubber band) up
to the pivot, and the magnitude of the initial angular momentum of the car about the pivot is
After the collision, the car is stopped, and the pendulum is rotating with some initial angular
speed
ω
. The pendulum has angular momentum
L=I
ω
(6).
4. Kinetic Energy
The initial kinetic energy (KE
o
) of the car is
After the collision, the car is stopped, and the pendulum is rotating with some initial angular
speed
ω
. The pendulum rotational kinetic energy is
5.Potential Energy
When a point mass increases its height by an
amount
h
, it increases its gravitational potential
energy (PE) by an amount
mgh
. For a non-point
mass like the physical pendulum, the distance
h
is
the amount the center of mass moves upward.
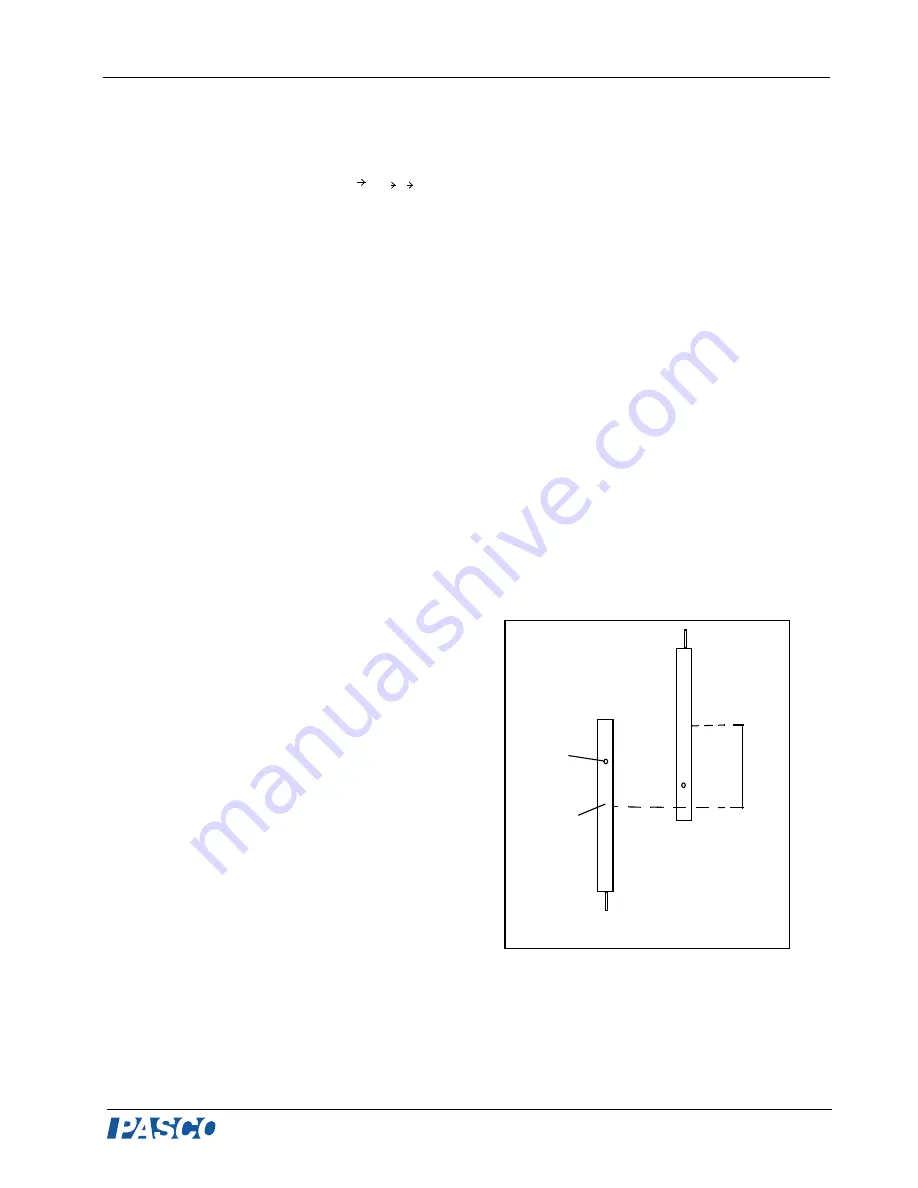
For a complete 180
o
rotation (Figure 8), that
distance
h=2x
, and thus the gain in potential
energy is
Experiment
1. Adjusting the release height on the track.
Release the car from half the way up the hill,
so that the pendulum does
not
hit the top
support peg. Repeat, releasing the car from a higher elevation each time, until the
pendulum "just" makes it to the top. You will need to use the marker on the white board to
keep track of your position. If you do it just right, you can get the pendulum to stop upside
down. If the pendulum hits the top peg and bounces off, your release point was too high.
L
rxp
=
L
o
=m
o
v
o
r
(5).
KE
o
=
½
m
o
v
o
2
(7).
KE=
½
I
ω
2
(8).
x
x
h=2x
Before
After
pivot
center of
mass
Figure 8
PE = 2Mgx
(9).































