PASCO ME-9430, Instruction Manual And Experiment Manual

Page: 23 / 30

012-04840E
Dynamics Cart
19
®
!
Experiment 6: Sliding Friction and
Conservation of Energy
EQUIPMENT NEEDED:
– Dynamics Cart (ME-9430) – Stopwatch (SE-8702)
– Metric tape (SE-8731) – Brick or block of wood
– Long board that can be used as a ramp – Friction Block (003-04708)
– Protractor
Purpose
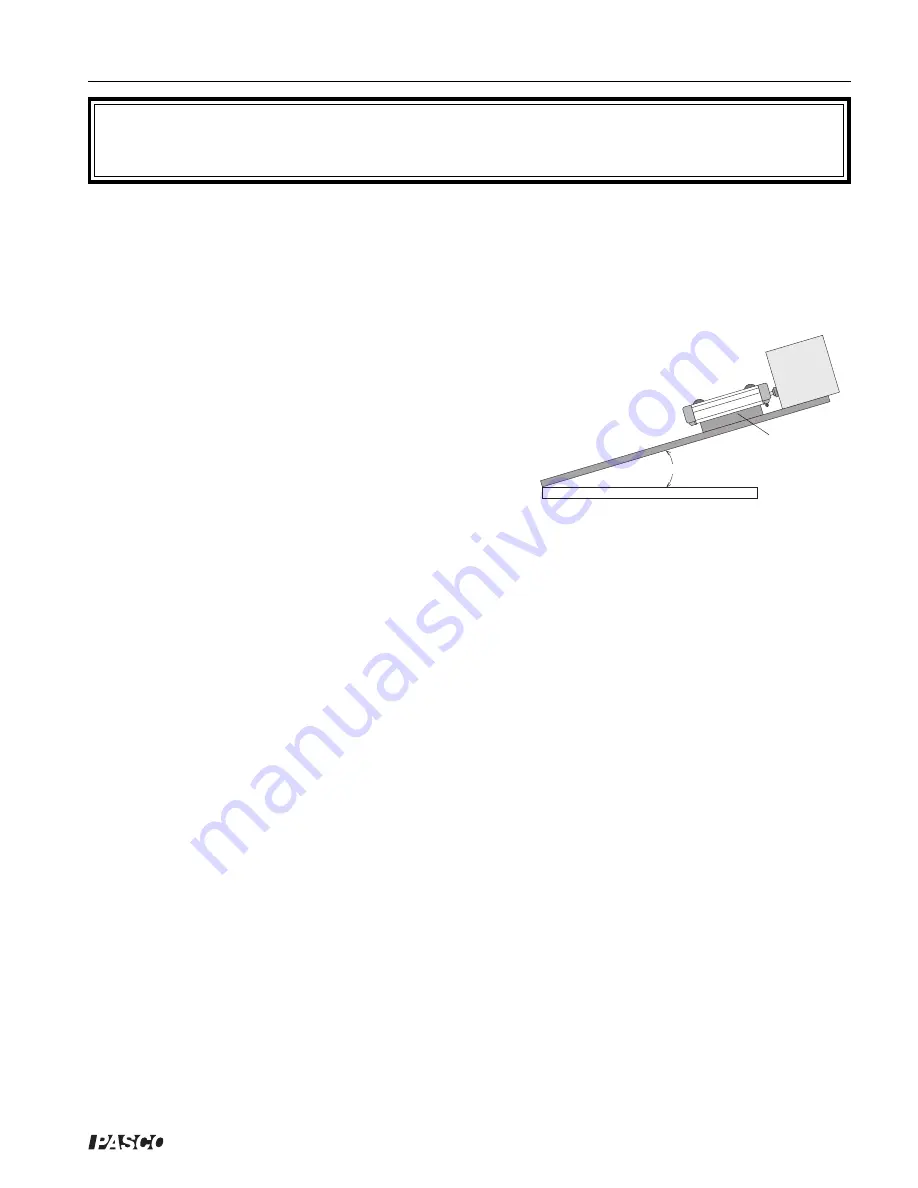
In this lab, the Dynamics Cart will be launched down a
ramp, as shown in Figure 6.1, while riding on a friction
block. The initial elastic potential energy and gravitational
potential energy of the cart are converted to thermal energy
as the cart slides to a stop. The thermal energy generated on
the surfaces is the same as the work done against sliding
friction.
Theory
Using the principle of conservation of energy, we can equate the initial energy of the system with the final
(i.e. thermal) energy of the system. This leads to:
1/2kx 2 + mgDsin
θ
= µ
k
mgDcos
θ
(EQN-1)
(elastic P.E.) + (gravitational P.E.) = (work done against friction)
where
k
is the spring constant of the plunger (from Experiment 4),
x
is the distance that the plunger is pushed
in, m is the mass of the cart plus the friction block, D is the distance that the block slides after the cart’s plunger
is released,
θθθθθ
is the angle of the ramp to the horizontal, and µ
k
is the coefficient of kinetic or “sliding” friction.
In this experiment, you will use the principle of the conservation of energy to predict
D
, given certain measure-
ments you will make and the value of k determined in Experiment 4. First you will need to determine the
coefficient of kinetic or “sliding” friction for the friction block.
Determining µ
k
: If the angle of the ramp is high enough, the friction block will slide down the ramp with
uniform acceleration due to a net force on the block. The net force on the block is the difference between
the component of the gravitational force (mgsinø) that is parallel to the surface of the ramp and the friction
force (-µ
k
mgcosø) that retards the motion . The angle ø is the angle of the ramp when the block slides
down the ramp with uniform acceleration. The acceleration down the ramp is given by:
a = gsinø - µ
k
gcosø
(EQN-2)
The average acceleration down the ramp is given by:
a = 2d/t
2
(EQN-3)
where
d
is the total distance the block slides and
t
is the time required to slide through that distance. If the
acceleration is uniform, EQN-2 equals EQN-3 . You can use the measured values of the angle ø (the angle of
uniform acceleration), the distance d , and the time t to calculate the kinetic coefficient of friction µ
k
.
Figure 6.1
friction block