Smart Timer
012–06734A
26
I
=
τ
α
To find the rotational inertia experimentally, a known torque is applied to the object and the
resulting angular acceleration is measured. Since
!
= I
"
,
where
"
"
is the angular acceleration, which is equal to
a/r,
and
!
is the torque caused by the
weight hanging from the thread that is wrapped around the base of the apparatus.
τ
=
rT
where
r
is the radius of the 3-Step Pulley about which the thread is wound and
T
is the
tension in the thread when the apparatus is rotating.
Applying Newton’s Second Law for the hanging mass,
m
, gives (See Figure 4.2)
Σ
F
=
mg
–
T
=
ma
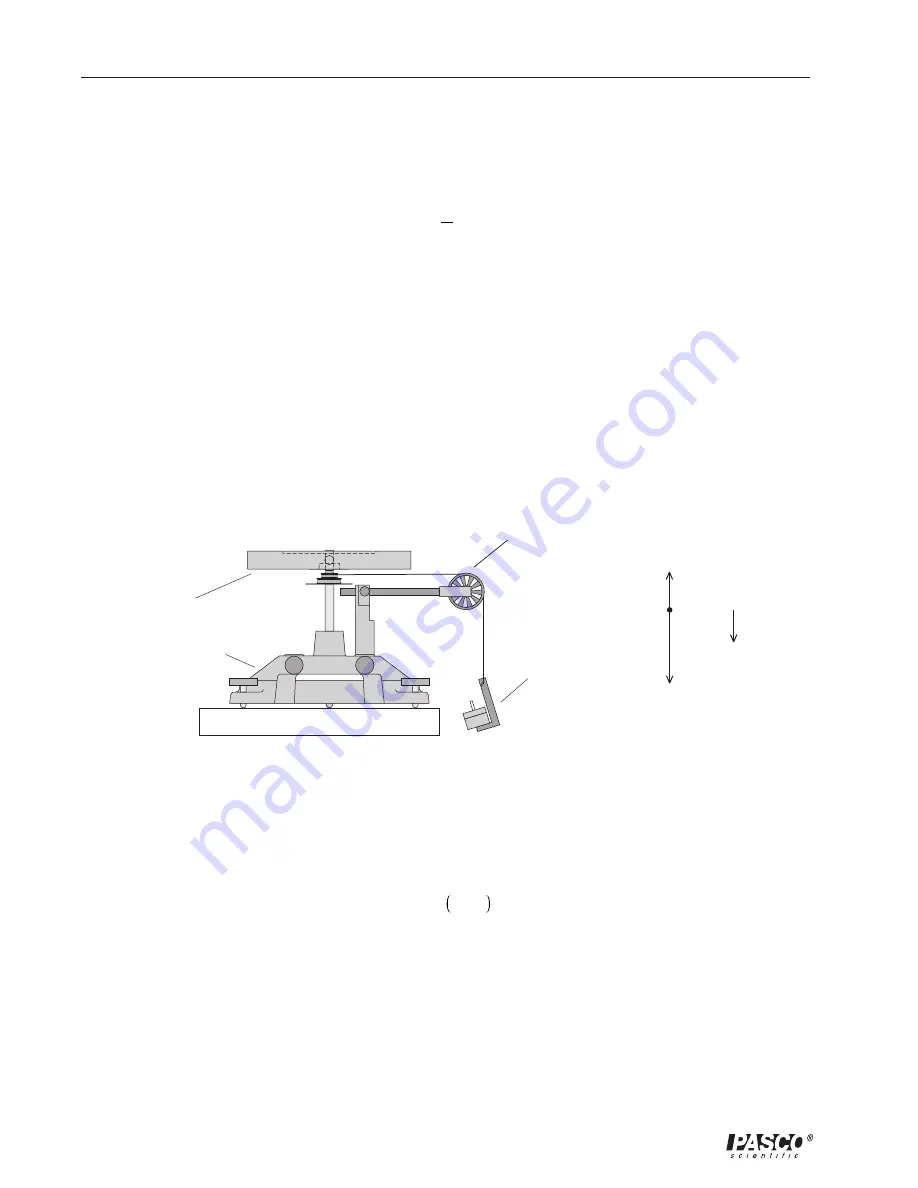
Figure 4.2
Rotational Apparatus and Free-Body Diagram
rotational
disk
"A" base
hanging
mass
mg
T
a
Solving for the tension in the thread gives:
Once the linear acceleration of the mass (
m
) is determined, the torque and the angular
acceleration can be obtained for the calculation of the rotational inertia.
T
=
m g
–
a
Smart Pulley
Summary of Contents for ME-8930
Page 2: ...Smart Timer 012 06734A ...
Page 9: ...012 06734A Smart Timer 5 ...
Page 13: ... 011 A01 011 BC DC E 2 0 F 0 1 0 1 2 2 0 1 234 3 5 3 353 2 0 6 07 8 35 53 2 9 ...
Page 18: ...Smart Timer 012 06734A 14 ...
Page 28: ...Smart Timer 012 06734A 24 ...
Page 34: ...Smart Timer 012 06734A 30 ...
Page 40: ......





































