15 - PVD3627-August 2011
3.1.4.
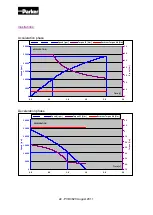
A MGV motor shows two phases during its acceleration (resp. deceleration) time:
Acceleration – Deceleration time with MGV motors
- from 0 to the
Base speed
during its acceleration (or inversely from the
Base speed
to 0 during its deceleration), the phase is called “at constant Torque”.
- from the
Base speed
to the
Maximal speed
during its acceleration (or inversely from
the
Maximal speed
to the
Base speed
during its deceleration), the phase is called “at
constant Power” or “Spindle mode”.
We assume that the resistant torque is maintained constant and that the motor is
able to provide it during the whole acceleration (resp. deceleration) phase. So the
calculation of the total acceleration (resp. deceleration) time can be separated in two
parts as explained below. When the resistant torque is not constant, the calculation
becomes more complex and can be made through iterative means.
N
base
Base speed
of the motor [rpm]
Notations:
Ω
base
Base angular speed of the motor [rad/s]
∑
J
Total inertia {motor rotor i load inertia reflected to the motor} [kgm²]
M
motor
equal to
M
S6
(peak torque) for a short acceleration (deceleration) time,
otherwise
M
S1
(constant torque) [Nm]
M
resistant
Resistant torque, considered as constant during the whole acceleration
(resp. deceleration) phase [Nm]
M
Torque available for the acceleration (respectively deceleration) [Nm]
N
max
Maximal speed
of the application [rpm]
Ω
max
Maximal angular speed of the application [rad/s]
P
motor
equal to
P
S6
(peak power) for a short acceleration (deceleration) time,
otherwise
P
S1
(constant power) [W]
P
Power available for the acceleration (respectively deceleration) [W]
t
1
Acceleration (respectively deceleration) time “at constant Torque” [s]
t
2
Acceleration (respectively deceleration) time “at constant Power” [s]
∆
t
Global acceleration (respectively deceleration) time [s]
60
*
*
2
base
base
N
π
=
Ω
Angular speeds:
60
*
*
2
max
max
N
π
=
Ω
3.1.4.1. Constant Torque Phase – t
1
calculation
t
resis
motor
M
M
M
tan
−
=
Acceleration time t
1
“at constant Torque” from 0 to the
Base speed
:
M
J
t
base
Σ
Ω
=
*
1
t
resis
motor
M
M
M
tan
+
=
Deceleration time t
1
“at constant Torque” from
Base speed
to 0:
M
J
t
base
Σ
Ω
=
*
1