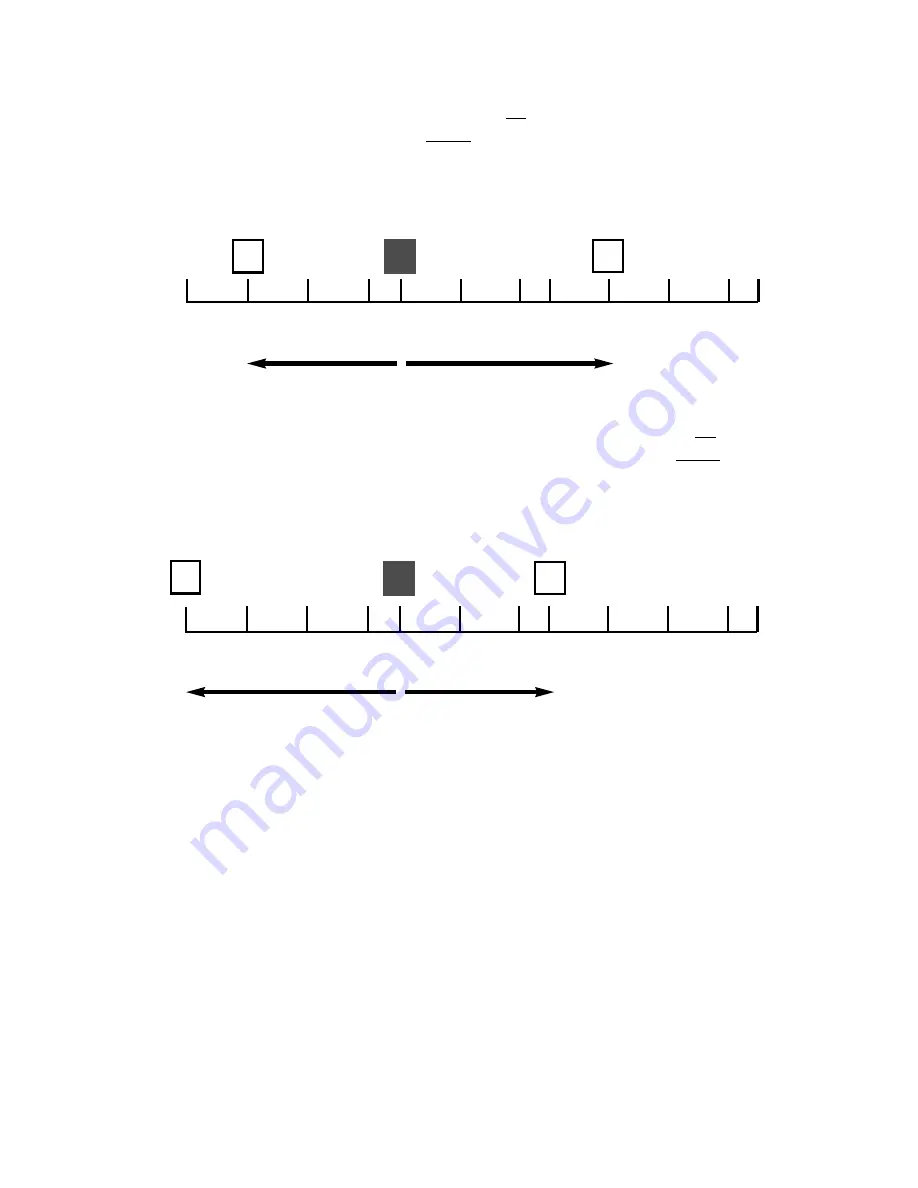
When we think of the letters on the circle of fifths as representing chord roots,
we see notes separated by intervals that create strong tonal movement. Moving
clockwise on the wheel, we go from C to G to D, etc. This movement can be
interpreted in two ways. First, if we are going up the scale, the interval from C to
G is a fifth. Second, if we are going down the scale, the interval from C to G is a
fourth.
On the other hand, if we move counter-clockwise on the wheel from C to F to B<
,
this movement can be interpreted in two ways. First, if we are going up the
scale, the interval from C to F is a fourth. Second, if we are going down the
scale, the interval from C to F is a fifth.
The descending fifth and the ascending fourth intervals produce a strong
resolving chordal movement. This movement is at the heart of many chord pro-
gressions. For instance, the I, IV, V, I chord progression in the key of C major
produces C, F, G and C. As already shown, the movement going counter-clock-
wise resolves at F. Similarly, the V chord (G) resolves back to the tonic C.
In the circle of fifths diagram you might have noticed that the relative minor of F
is D. In the chord substitution section of the Harmonizer, we can see that the
chord of Dm can substitute for F major. When we make the change, our I, IV, V, I
progression turns into a I, IIm, V, I progression: C, Dm, G and C.
You might now notice that on the outer ring of the circle of fifths diagram we can
read (going counterclockwise) the same root notes of the IIm, V progression fin-
ishing with the I chord (G, D, C). In fact, it goes beyond that. You can see that
the very popular IIIm, VIm, IIm, V7, I progression is derived from the circle of
fifths as well. In C major that progression would be Em, Am, Dm, Gdom7, C.
Down the scale
D
E
F
G
A
B
G
A
B
C
C
w
w
h
w
w
w
h
w
w
w
h
2½ steps = 4th
3½ steps = 5th
{
{
Down the scale
Up the scale
D
E
F
G
A
B
G
F
A
B
C
C
w
w
h
w
w
w
h
F
w
w
h
2½ steps = 4th
3½ steps = 5th
{
{
Up the scale
w
35






































