16
09
Approximate solutions to Equations
of higher degree
(Newton’s method)
Newton’s method is used to calculate approximate solutions to the equation
. For a
initial value
, the following recurrence relation gives successive approximate solutions:
It should be noted that the series calculated above may not always converge, depending on
the initial value
.
Program
?→ X:Lbl 1:X -(
)÷(
)→ X:
X
Goto 1 <
40 STEP
>
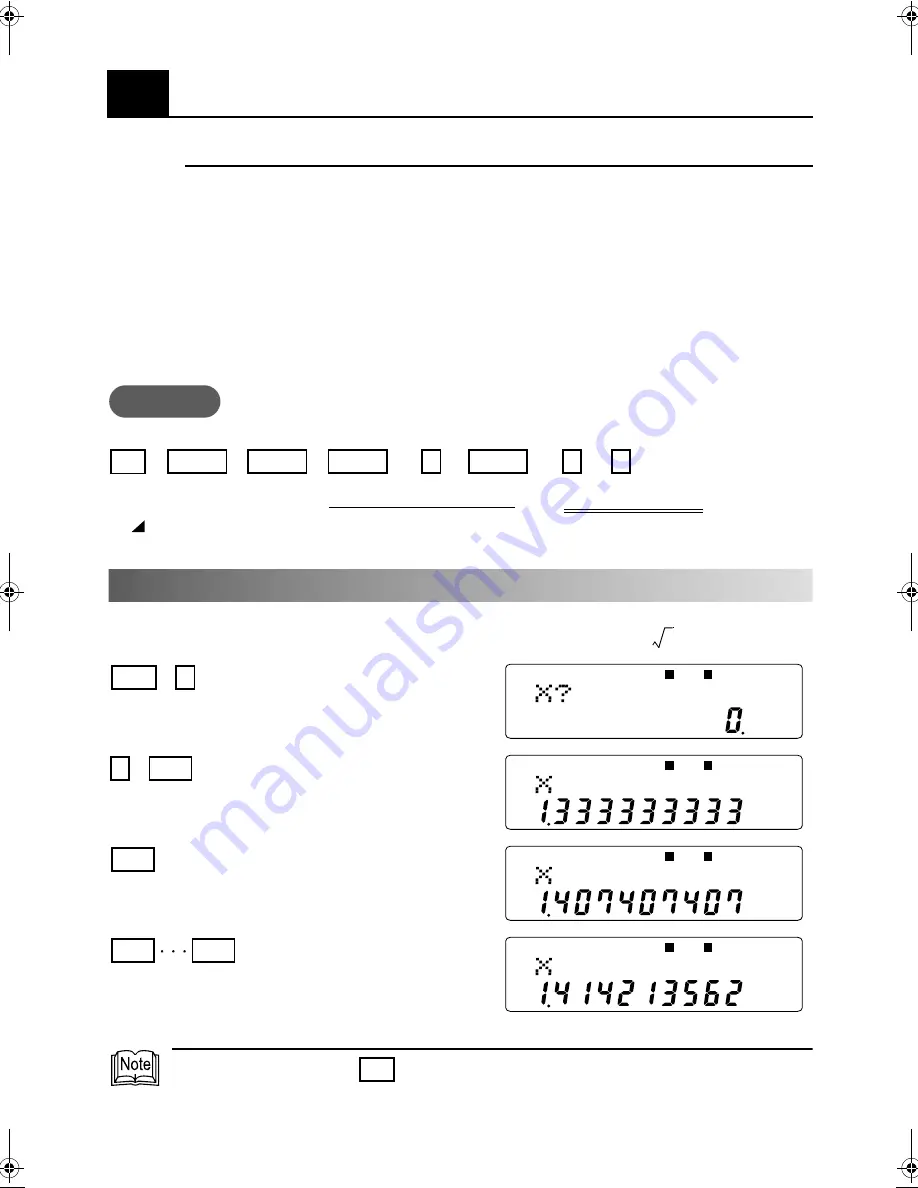
Execution Example:
Find solutions to the equation
. (Solutions are
and )
To stop program, press the
key.
To calculate for other functions, enter the apropriate function in the part indicated by a single
underline, and the derivative in the part with double underline.
f x
( )
0
=
x
1
x
i
1
+
x
i
f x
i
( )
f
′
x
i
( )
------------
–
=
x
1
ON
MODE
MODE
MODE
1
PRGM
MODE
1
COMP
1
P1
X
3
-2 X
2
-2 X +4
3 X
2
-4 X -2
x
3
2
x
2
–
2
x
–
4
+
0
=
2
±
2
Prog
1
S A
D R
P1
P1 P2 P3 P4
G
1
EXE
Disp
S A
D R
P1
P1 P2 P3 P4
G
EXE
Disp
S A
D R
P1
P1 P2 P3 P4
G
EXE
EXE
Disp
S A
D R
P1
P1 P2 P3 P4
G
AC
関数電卓事例集
.book
1
6
ページ
2002年9月2日 月曜日 午後6時51分
Summary of Contents for 3950P
Page 1: ......
Page 46: ...MEMO MEMO MEMO MEMO...
Page 47: ...Authors Dr Yuichi Takeda Research and Development Initiative Chuo University...
Page 48: ......