IM 2769-10E
―
13
―
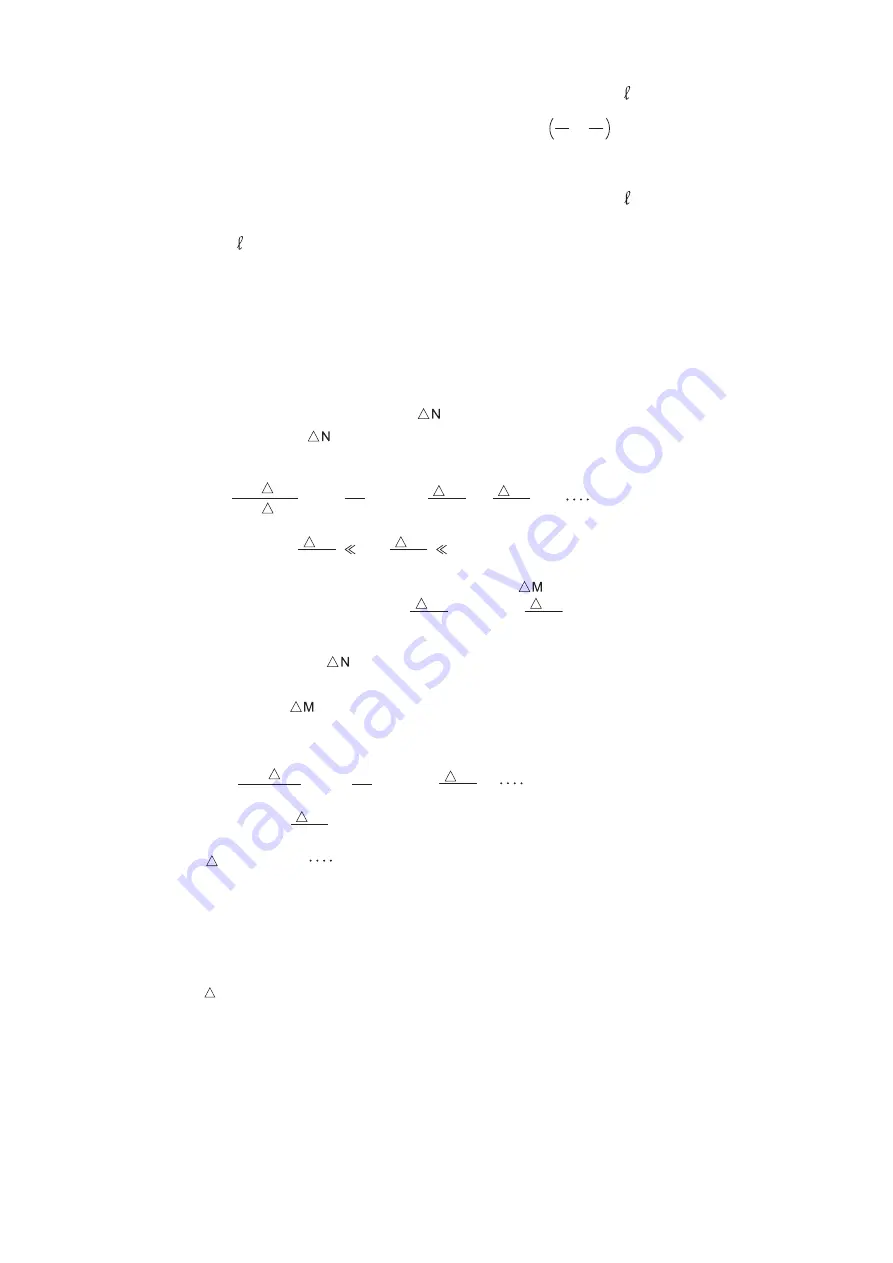
When the value of S is small, namely, X is small, and if the value of
/S is large,
a large error will cause no matter how small the value of
N
M
n
m
–
may be.
In case of low resistance measurement, the lead resistance between
Ps and C
2
is designed to be nearly zero.
Therefore, the lead resistance from C
2
to Rx may be considered as .
In this view, when this double bridge is used in the × 0.0001 range,
arrange"
" to be less than 10 mΩ.
6.2.2 Error due to Potential Lead
When the potential lead resistance is large and cannot be neglected, the lead connected across
the potential terminals P
1
and P
2
becomes an error of the M and N arms.
While, the individual resistance of M and N arms are not directly related to this error but
the ratio N/M has relation to the error.
Therefore, when the lead resistance
is present on the N arm,
the influence of this
can be cancelled by adding a lead resistance to the M arm.
This is expressed by the following equation.
(6.4)
X = × S = × S (1 + )
–
(M + M)
(N + N)
N
N
N
N
M
M
on condition that,
1,
M
M
1
N
M
In Model 2796 double bridge, a resistance to act as
can be connected to the terminals P
2S
.
The error becomes minimum when
M
M
is equal to
N
N
based on equation (6.4).
Then, find the value of
for the measurement where the error due to
the potential lead is 0.5% of the measured value without connecting a resistance
corresponding to
.
(6.5)
(6.6)
X = × S = × S (1 + )
From equation (6.4),
The value of should be 1.005. Therefore,
M
N + N
N
N
N
N
(1 + )
N = 0.005N
N
M
Model 2769 bridge is designed so that the N = 21 Ω
when the measuring dial scale is minimum (1.0).
Substituting N = 21 Ω for
equation (6.6),
N = 110 m
Ω


















